基于北斗三频约束的中长基线解算研究

金俭俭，高成发

(东南大学 交通学院，江苏 南京 211189)

随着GPS，BDS，GLONASS，GALILEO各卫星导航系统的不断完善和发展，全球卫星导航定位系统GNSS(Global Navigation Satellite System)正迈入多系统多频定位时代[1]。多系统融合定位，提高观测卫星的图形强度，保证定位的精度及可靠性，减少或者消除单系统中导航定位产生的系统误差。而如何进行多系统观测数据的融合，是成功实现基线解算的关键；多频观测值能够形成一系列具有较优性质的观测值组合，主要体现在波长较长、大气误差对模糊度解算影响较小等方面，同时多频观测值组合为基线解算中周跳探测以及模糊度的固定提供了更多高效可行的方法。目前，BDS是唯一全星座播发三频信号的卫星系统，如何利用BDS三频观测值，建立具有BDS三频约束的GNSS基线解算模型，实现多系统组合模糊度快速固定，对于推广我国BDS系统应用具有重要意义。

1 北斗模糊度解算

1.1 北斗三频组合观测值

考虑电离层和对流层对卫星信号折射的影响，得到载波双差观测方程为

Δφ(i,j,k)=Δρ+ΔT-η(i,j,k)·ΔI+

λ(i,j,k)·ΔN(i,j,k)+Δεφ(i,j,k).

(1)

式中：η(i,j,k)为组合观测值的电离层延迟因子，Δεφ(i,j,k)为其余残余误差。

三频组合观测值为

Δφ(i,j,k)=(i·f1·Δ▽φ1·j·f2·Δφ2+

k·f3·Δφ3)/f(i,j,k).

(2)

三频组合模糊度为

ΔN(i,j,k)=i·ΔN1+

j·ΔN2+k·ΔN3.

(3)

三频组合观测值的频率与波长表示为

(4)

通常认为北斗各个频段上观测值精度相同，将其设为σ△▽φ，则观测值的精度计算为

σ△▽(i,j,k)=

=μ(i,j,k)σ△▽φ.

(5)

式中：μ(i,j,k)为组合观测值的噪声放大因子。

对北斗3个频段上的观测值进行相关线性组合，可以得到以下几种常见的组合形式。组合结果如表1所示。

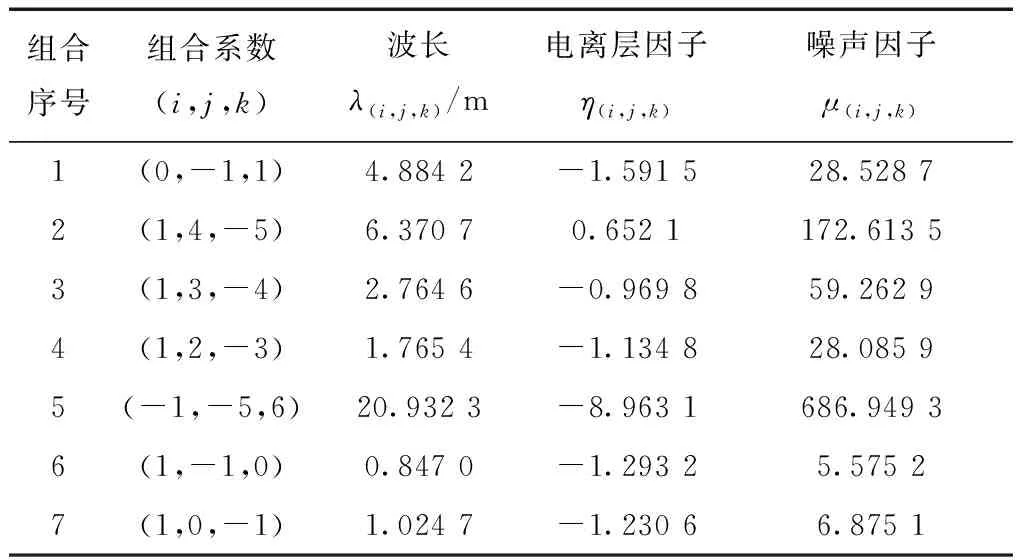
表1 BDS超宽巷/宽巷载波组合

1.2 BDS超宽巷模糊度解算

对于BDS三频观测值，利用载波与伪距组合，可以求解北斗超宽巷组合模糊度为

Δ

(6)

若精度仅受伪距与载波观测值影响，则求解模糊度精度为

(7)

对于非差载波相位、伪距观测噪声误差分别为0.002 m和0.3 m，依据误差传播定律，可以知道，载波相位与伪距观测值噪声误差分别为0.004 m和0.6 m[2]，误差为0.173 7周，因而单历元对模糊度取整即可正确固定北斗的(0,-1,1)组合超宽巷模糊度。

由于对流层残余误差对中长基线影响较小，为提高定位精度，采用最小二乘平差思想，用北斗的超宽巷模糊度ΔN(1,4,-5)约束求解。

(8)

其中，A为设计矩阵；δx为基线未知参数，按照传统求解模糊度的方法，单历元形成误差方程求解模糊度值。

(9)

1.3 北斗基础模糊度固定

对于一般的短基线，对流层残余误差可以不考虑，使用两个超宽巷组合及两个消电离层组合，可以单历元求解BDS的3个基础模糊度[2]，但是对于中长基线，单一历元是无法正确固定基础模糊度的。这里可以利用滤波思想，多历元平滑无电离层组合模糊度NIF。

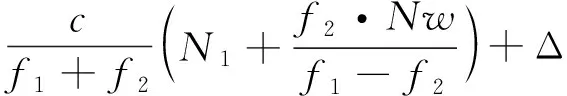
(10)

其中，多历元平滑求得的无电离层组合模糊度，可以从中分离出BDS的基础模糊度。算式为

(11)

Nw为第一与第二频段组合的宽巷模糊度，当Nw=ΔN(1,0,-1)时，即可求解出BDS的N1与N3基础模糊度。

2 固定GPS基础模糊度

当BDS的基础模糊度解算固定好后，可与GPS系统卫星相应的观测方程联立，求出GPS的基础模糊度。实验中选取固定好的BDS基础模糊度，利用消电离层组合，解算基线向量信息；构建附有BDS三频约束的基线解算模型。这样可以降低基线解算模型中法方程的病态性，有效实现GPS基础模糊度的快速固定。同时为了提高模糊度解算的精度，将伪距与载波观测方程联立，根据伪距与载波相位的测量精度，采用经验定权法，比值取1∶100[3]。综合约束模型为

(12)

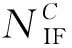
对于GPS浮点模糊度，可以单历元取整固定，也可使用LAMBDA算法固定其基础模糊度，求解基线向量。

3 实验分析

实验数据采用南京计量院CORS站JN_NF与LH_NF于2016-12-07所采集的一组GPS/BDS/GLONASS中等基线数据，其中BDS包含3个频点的观测值，基线长度为41.5 km，数据的采样率为1 s。两站点分布如图1所示。

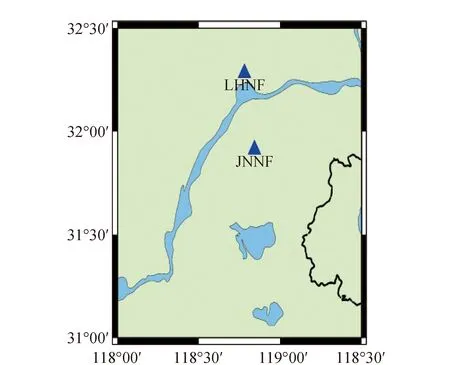
图1 基站站点分布

实验中，两站点的坐标精确已知，可使用GAMIT软件，精确求解基线向量。在精确的基线向量解确定好之后，可以按照网络RTK模式求解宽巷或者超宽巷模糊度。将实验中计算出来的模糊度浮点解与已知固定解进行比较，可以得到相关模糊度偏差值。

从图2中可以看出，按照三频宽巷定义法解算的(0，-1，1)组合超宽巷模糊度，其偏差值基本稳定在±0.15周之内，四舍五入便可获得准确的超宽巷Δ▽N(0,-1,1)模糊度值。在精确求解北斗超宽巷模糊度后，利用最小二乘原理(式8)，约束求解(1，4，-5)组合模糊度。从图3中可以看出，该组合模糊度偏差值基本稳定在0.2周之内。将两者进行对比，发现(1，4，-5)组合模糊度偏差，总体略大于(0，-1，1)组合模糊度偏差，这是因为利用最小二乘求解(1，4，-5)组合模糊度时，解算过程受到了(0，-1，1)组合观测噪声的影响，使得最后解算的精度略差。

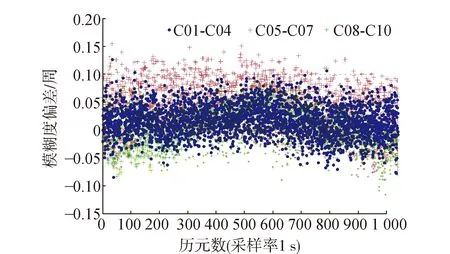
图2 北斗超宽巷Δ▽N(0,-1,1)模糊度偏差

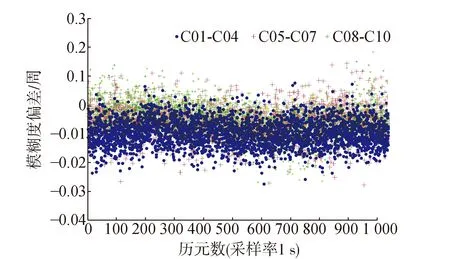
图3 北斗Δ▽N(1,4,-5)模糊度偏差

在准确求解出北斗的两个超宽巷模糊度后，求解两个宽巷模糊度，在多历元平滑无电离层组合模糊度之后，可以从中分离出北斗的各个基础模糊度。鉴于篇幅有限，这里只给出北斗B1频段的基础模糊度值偏差，如图4所示。

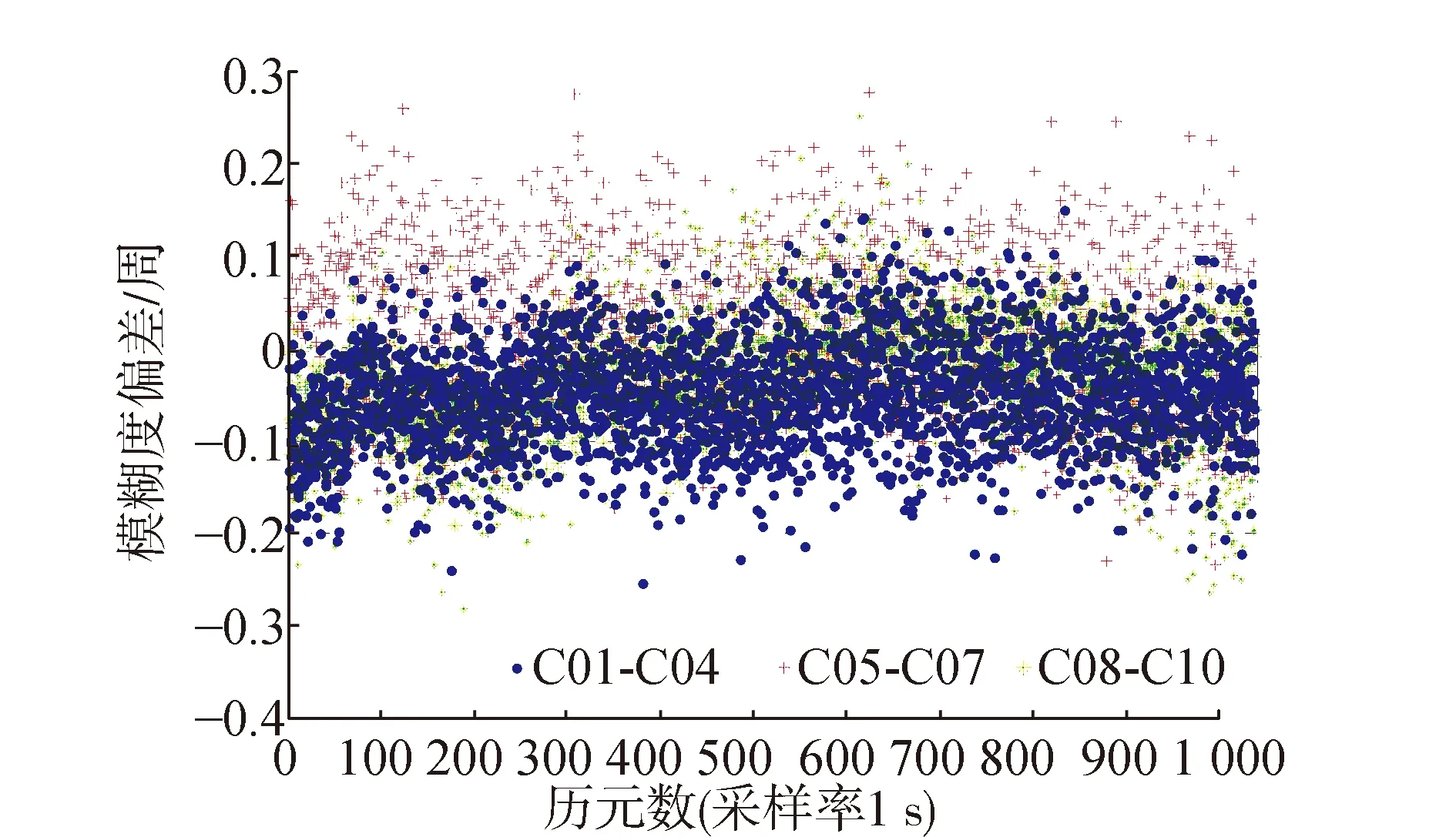
图4 北斗B1频段基础模糊度偏差

从图4中，可以看出，北斗B1频段基础模糊度偏差也大都在0.2周之内，对求解出来的北斗基础模糊度无需进行复杂的模糊度搜索工作，只需取整固定即可。

在北斗的基础模糊度求解完成之后，可将其作为先验知识，构建附有BDS三频约束的基线解算模型。图5中给出了GPS第一频段L1上基础模糊度偏差，从图5中可以看出，基础模糊度偏差大都在0.3周之内。较北斗基础模糊度，其模糊度偏差值增大。基线长度的增加，残余的电离层延迟直接影响到模糊度解算的精度，且相关的对流层延迟模型并不能很好地反演大气折射延迟，最终导致GPS基础模糊度偏差值偏大。

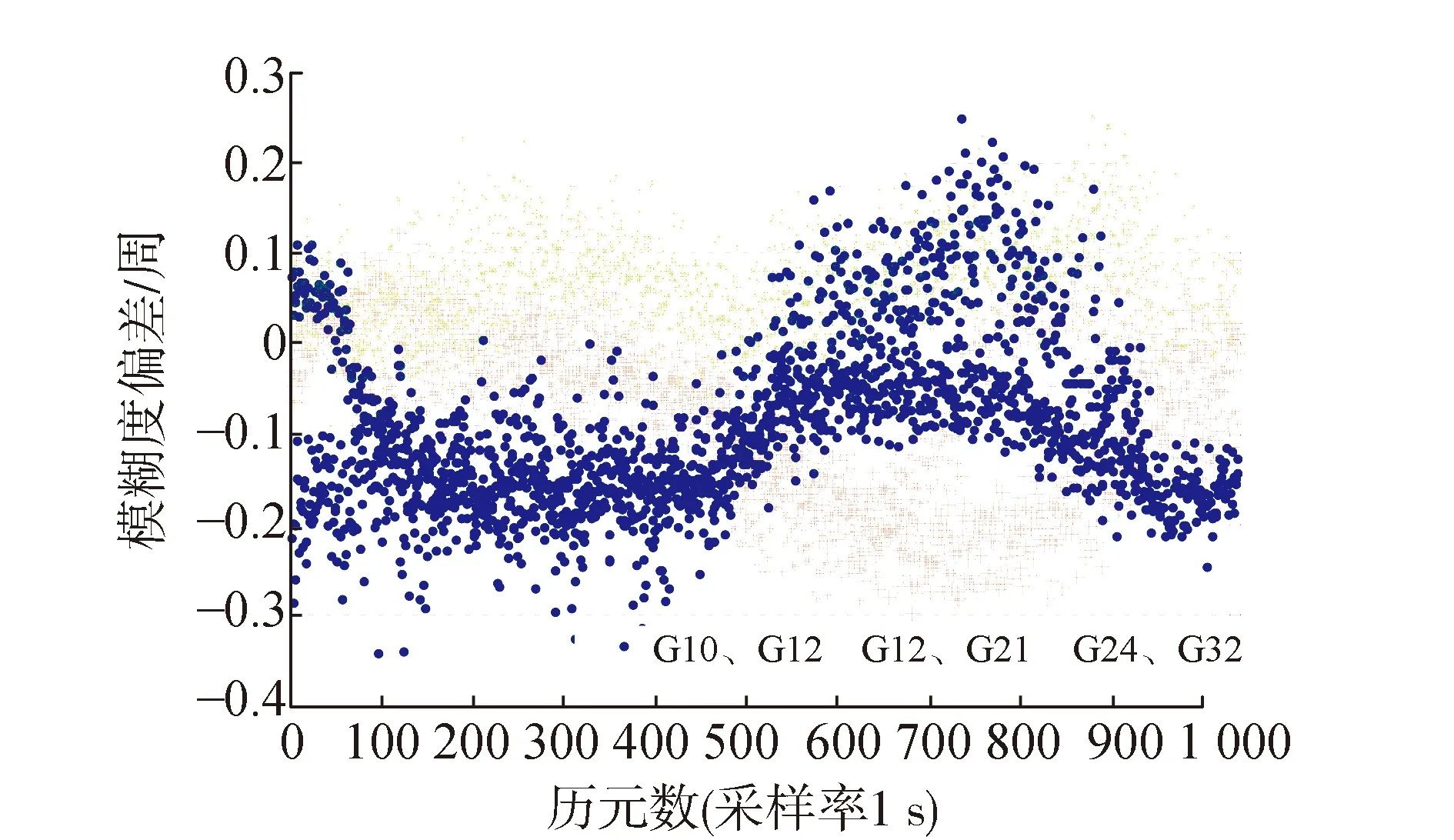
图5 GPS基础模糊度偏差

考虑模糊度求解的准确性，对求解出来基础模糊度，不采用取整固定，而是结合GPS双差模糊度浮点值与其协方差矩阵，利用LAMBDA算法搜索固定其基础模糊度，从而提高定位结果的可靠性。最后将GPS与BDS的基础模糊度回带消电离层观测方程中，求解基线向量，并与已知值(两个站点坐标已知)比较，可以得出基线解算偏差，如图6所示。从图6中可以看出，平面的定位精度在1.5 cm之内，高程方向比平面稍弱，在2 cm左右，整体上未出现较大偏差，也可说明模糊度的求解是可靠的。图7中给出了基线解算各方向中误差，平面上中误差在2～8 mm，高程方向为6～12 mm，与基线解算各方向偏差一致。

图6 基线解算各方向偏差

图7 基线解算各方向中误差

本次实验中，快速固定GPS与BDS基础模糊度需几个历元，而传统的卡尔曼滤波对基线进行求解时(如表2所示)，需要数十历元才能正确固定好模糊度。因此，本文方法，能快速求解基础模糊度，大大缩小正确固定模糊度所需的原始观测数据量，实现基线的快速解算。

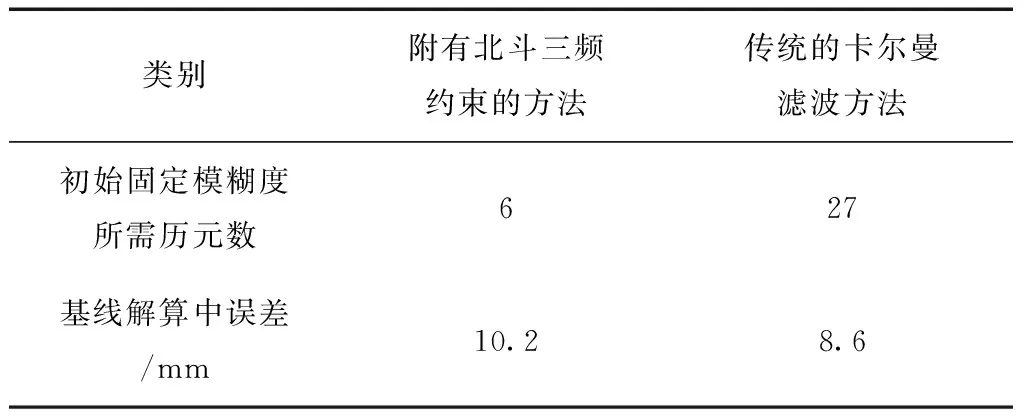
表2 卡尔曼滤波与文中方法对比

4 结 论

本文以BDS三频为核心，介绍BDS两个超宽巷模糊度求解方法，并阐述在中长基线下，如何利用BDS的两个超宽巷模糊度快速求解其基础模糊度。将BDS的基础模糊度作为先验知识，约束求解GPS的基础模糊度，进行基线向量的求解。并用北斗实测三频数据进行验证。

1)对于北斗(0，-1，1)三频组合观测值，通过宽巷载波与窄巷伪距组合，消除电离层与对流层延迟，单历元解算的模糊度偏差在0.15周之内，模糊度固定成功率达100%。

2)利用最小二乘平差原理，用北斗的超宽巷模糊度约束求解模糊度偏差控制在0.2周之内，可单历元取整固定。

3)将北斗的两个超宽巷模糊度进行相关线性组合，可以得到宽巷模糊度，再通过多历元平滑消电离层组合模糊度，可快速分解出北斗的基础模糊度。

4)将准确求解的北斗基础模糊度作为先验知识，构建消电离层组合，同时加入伪距观测方程，构建附有BDS三频约束的基线解算模型，可以加快GPS基础模糊度的求解。

5)本文提出的附有北斗三频约束的BDS/GPS双系统模糊度解算方法，可实现模糊度的快速固定，缩小了正确固定模糊度所需的原始观测历元数，同时可将其应用在多系统定位中，利用文中所提出的模型，快速解算出其它系统基础模糊度，最后进行多系统的融合基线解算。

[1] 高成发，胡伍生. 卫星导航定位原理与应用[M]. 北京：人民交通出版社，2011.

[2] 吕伟才, 高井祥, 王坚,等. 北斗三频约束的短基线模糊度单历元算法[J]. 中国矿业大学学报, 2015, 44(6):1090-1096.

[3] 黄令勇, 宁德阳, 吕志平,等. 两种长基线模糊度解算方法在北斗三频应用中的比较[J]. 大地测量与地球动力学, 2014, 34(5):101-105.

[4] 王生朝. 北斗三频模糊度解算方法研究[D]. 北京：中国矿业大学, 2015.

[5] TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1-2):65-82.

[6] 李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4):18-23.

[7] FENG Y. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J]. Journal of Geodesy, 2008, 82(12):847-862.

[8] 高旺, 高成发, 潘树国,等. 基于部分固定策略的多系统长距离基准站间模糊度快速解算[J]. 武汉大学学报(信息科学版), 2017, 42(4):558-562.

[9] 何俊, 刘万科, 张小红. 北斗短基线三频实测数据单历元模糊度固定[J]. 武汉大学学报(信息科学版), 2015, 40(3):361-365.

[10] ODOLINSKI R, TEUNISSEN P J G, ODIJK D. Combined GPS + BDS for short to long baseline RTK positioning[J]. Measurement Science & Technology, 2015, 26(4).

[11] 姚一飞, 高井祥, 李增科,等. 基于模糊度相关法的北斗三频载波单历元基线解算[J]. 武汉大学学报(信息科学版), 2016, 41(11):1433-1439.

[12] HAN S, RIZOS C. Single-Epoch Ambiguity Resolution for Real-Time GPS Attitude Determination with the Aid of One-Dimensional Optical Fiber Gyro[J]. Gps Solutions, 1999, 3(1):5-12.

[13] 王霞迎. BDS/GPS基线解算算法研究[D]. 北京：中国测绘科学研究院, 2014.

[14] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社，2014.

[15] 李征航. GPS测量与数据处理[M]. 武汉：武汉大学出版社, 2010.