基于多方向剖面线Douglas-Pucker算法简化的DEM综合方法

赵文豪,闫 利,张云生,陈斯炀

(1.武汉大学 测绘学院, 湖北 武汉 430079; 2.国家基础地理信息中心, 北京 100830； 3.中南大学 地球科学与信息物理学院, 湖南 长沙 410083 )

随着激光扫描技术和多视影像密集匹配方法的发展，获取高密度的点云越来越容易，为了减少冗余和提高数字高程模型(DEM)处理、网络传输等应用的效率，有必要对DEM进行综合以获取多尺度DEM数据库[1]。目前的DEM综合方法按照DEM存储方式可以大致分为2类：面向三角网(TIN)的综合方法和面向格网DEM的综合方法[2]。其中3维Douglas-Pucker (DP) 算法是由费立凡等人根据经典2维DP算法发展而来的DEM综合算法，最早用于处理离散点，也就是TIN表达形式的DEM[3-4]。由于原始算法处理海量数据时效率较低，何津在利用3维DP算法综合规则格网DEM时，利用行列扫描的方式来减少计算量[5]。该方法大幅提高了效率，但可能会出现漏掉重要地形点的情况。根据朱雪坚等人的研究发现，基准面的选择和扫描方向的选择对结果存在较大影响[6]。Ma等人认为高程剖面线可以在一定程度上反映DEM的全局特征，因此提出一种4方向剖面线DP简化方法来综合DEM[7]。该方法生成剖面线时依赖于VIP特征[8]，若VIP特征保留较少，4个方向的扫描难以确保扫描到全局的DEM特征。

针对以上问题，本文提出一种基于多方向剖面线简化的DEM综合方法。首先基于多方向剖面线DP简化算法提取DEM关键特征点，然后构建三角网再内插规则格网DEM，以达到DEM综合的目的。

1 实验数据

为了验证本文算法，本文采用如图1所示的两组由航空激光点云数据内插的格网DEM进行实验，内插过程采用surfer 8.0实现，选择克里金插值算法生成间距为2 m格网DEM。如图1(a)所示的数据1，格网大小为1 416像素×943像素，高程范围从1 125～1 623 m；如图1(b)所示的数据2，格网大小为913像素×555像素，高程范围是从1 500～2 115 m，两组数据地形起伏较大。

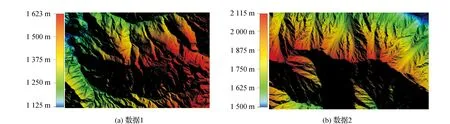
图1 实验数据

2 基于DP算法的DEM简化原理及其改进

2.1 DP算法简介

DP算法，是Douglas和Pucker在1973年提出的一种将二维曲线化简的算法[3]。DP算法主要有2种形式，其一为“锚点前进法”，另外一种为“分而治之法”，后一种方法效率更高[4]。因此本文采用后种方法，图2是其原理示意图。如图2所示的一条曲线，将这个序列中的首点A和末点J连成一条直线，然后计算序列中间各个点到这条直线的距离di。如果最大距离大于预先设置的阈值T(该阈值与简化后DEM要保留的精度相关，阈值越小，保留点越多，本文实验取经验值50)，设最大距离对应的点为S，然后对端点AS和SJ之间的点序列进行相同迭代操作，如果最大距离小于T则停止。最后将插入的端点与A、J连成折线替代原始曲线，从而起到简化的作用。

图2 二维DP算法原理图

2.2 基于多方向剖面线的特征提取

文献[7]以VIP特征为起点，向东南西北4个方向发射射线与DEM有效边界相交形成剖面线，然后进行DP简化。如果为了更好地覆盖整个DEM区域，最直接的方法是将DEM有效区域的每行的端点看成一条剖面线，然后采用2维DP算法简化，这类似于传统3维DP算法按照行列扫描的方式。为了获取更多方向的剖面线，本文不针对原始DEM直接运算，而是围绕原始DEM中心位置，按照一定角度间隔对原始DEM进行旋转。对于给定的角度θi，采用式(1)计算每个点旋转以后的坐标。

(1)

(2)

其中(X,Y)和(X′,Y′)分别是旋转前后的DEM水平坐标，(XC,YC)为旋转前DEM中心位置水平坐标。

提取特征后，采用式(2)对特征提取结果进行变换，以便于将特征提取结果重新纳入到原始DEM所在的坐标系，也便于融合所有旋转DEM提取的特征结果。图3(a)DEM为图1(a)所示DEM逆时针旋转15°的结果。进行DEM旋转后，只需要沿着新DEM水平方向生成剖面线即可实现多方向的剖面线生成。剖面线生成过程中，依次扫描新DEM的每一行，其起始点和终点为DEM有效区域。图3(b)为图3(a) 所示剖面线的高程剖面图。对于生成的每一条剖面线，采用如图2所示的2维DP算法进行简化以获得特征点，并保留每个特征点对应的距离，作为每个特征点的兴趣值R，以用于后续处理。

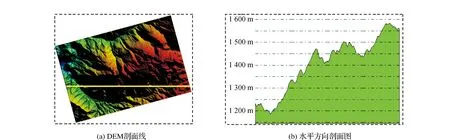
图3 DEM旋转结果与对应剖面线图

当旋转间隔较小时，相邻剖面线获取的特征点可能重叠，因此本文在完成多方向DP简化获得特征序列后，根据每个特征点记录的兴趣值，在局部进行极值抑制。具体过程为循环选取每个特征点，然后寻找其水平距离半径r(本文所有r取经验值3 m)范围的所有特征点集S，如果当前特征点的兴趣值R为S中的最小值或者最大值，则保留当前点，否则舍弃。经过抑制局部极值，局部范围内只保留一个特征明显的点。由于提取的特征点为离散3维点，不能用原始DEM搜索其邻域点。为了快速搜索每个点周围邻域内的点，本文采用K-D树进行搜索[9]。

综上所述，本文基于多方向剖面线简化的特征提取过程可以归纳为图4所示的流程。

如图5所示为按照30°角度间隔对图1(a)所示DEM进行多方向特征提取的结果。图5(a) 为多方向剖面线DP简化后直接叠加的结果，一共有32 739个点，进行局部抑制极值后，保留6 458个点，结果如图5(b)所示。

图4 多方向剖面线简化特征提取流程图

图5 特征点提取结果示意

获得DEM的特征点后，将这些点构建三角网，然后再采用线性内插的方式生成10 m大小格网的DEM，即为本文方法DEM综合的结果。

3 实验结果及分析

3.1 评价指标

获得综合后的规则格网DEM，分别采用高程中误差、平均坡度对结果进行定量评价；采用等高线套合对综合以后的DEM进行可视化定性分析[10]，指标定义如下：

1) 高程中误差：通过比较简化以后DEM上每个格网点高程与原始DEM对应位置的高程计算而来。

2) 坡度均值差：指简化以后的DEM坡度平均值，与原始DEM的坡度平均值进行比较的差值。差值越大说明与原始的DEM吻合越低，则DEM简化过程中，特征保留效果越差。

3) 等高线套合：分别对比简化后DEM生成等高线与原始等高线套合在原始DEM上的吻合程度，从整体上定性分析综合前和综合后的等高线。吻合程度越高，则表明综合后特征保留越好。

3.2 结果与分析

利用DP算法进行DEM特征点提取，传统做法多采用0°和90°方向联合提取，本文通过一定间隔角度旋转，可以进行多方向剖面线DP简化。本文对不同间隔角度进行了实验，最后选取15°、30°、45°间隔的结果进行定量和定性评价。

1) 定量评价结果。 高程中误差和坡度均值差如表1所示。从表1结果可以看出高程中误差随着旋转角度间隔的增大而增大。结果表明多方向的DP算法的精度比传统的算法要高。表1中坡度均值差也表明多方向简化结果比传统两个方向的结果精度高。

表1 定量评价结果

2) 定性评价结果。 图6是传统方法和本文方法重构DEM等高线套合结果；图7为等高线套合局部放大结果(蓝色为传统方法重构DEM的等高线，红色为原始的DEM等高线，绿色、紫色、淡紫色分别为45°、30°、15°多方向的DP算法重构DEM等高线)。从所得的等高线套合情况可以看出蓝色等高线偏离红色等高线最多，其余颜色的等高线与红色等高线走势更加吻合。从图7的局部放大结果中也可以明显看出蓝色与红色的吻合没有其余颜色与红色吻合得好。

图6 等高线套合效果

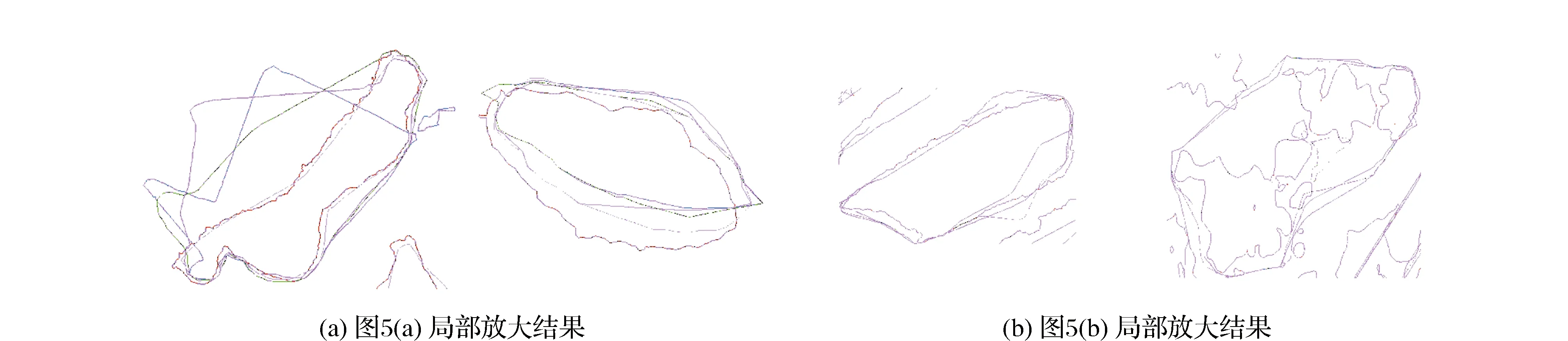
图7 等高线套合局部放大结果

实验结果表明本文所提出的多方向DP算法内插的DEM比传统的DP算法内插的DEM的精度更好。传统的DP算法内插时只考虑了2个方向，而本文方法通过格网DEM的旋转可以获取多方向剖面线的整合结果。故而用多方向算法得到的重构DEM比起传统算法得到的重构DEM更接近原始DEM。

4 结 论

针对DEM综合的问题，本文提出一种利用多方向剖面线DP算法简化提取特征点的方法，从实验结果可看出，不管是从高程误差统计还是坡度均值上，都可以看出本文方法得到的DEM与原始DEM地形形态更加吻合，能更好地保持地形形态特征。

本文在DEM综合时，只考虑了特征点，进一步将加入线特征，使得综合后的DEM能够更好地保持原始DEM特征。

[1] ZHOU Q, CHEN Y. Generalization of DEM for terrain analysis using a compound method [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011,66(1),38-45.

[2] 董有福, 汤国安.利用地形信息强度进行DEM地形简化研究[J].武汉大学学报(信息科学版), 2013,38(3):353-357.

[3] DOUGLAS D H, PEUCKER T K., Algorithms for the reduction of the number of points required to represent a digitized line or its caricature [J]. The Canadian Cartographer, 1973, 10(2):112-122 .

[4] 费立凡,何津,马晨燕,等.3维Douglas-Peucker算法及其在DEM自动综合中的应用研究[J].测绘学报, 2006(3): 278-284.

[5] 何津,费立凡.再论三维Douglas-Peucker算法及其在DEM综合中的应用[J]. 武汉大学学报(信息科学版), 2008 (2):160-163.

[6] 朱雪坚,叶远智,汤国安.运用三维Douglas-Peucker算法提取DEM地形特征[J].测绘通报,2014(3):118-121

[7] MA T, CHEN Y, HUA Y, et al. DEM generalization with profile simplification in four directions[J]. Earth Science Informatics, 2017, 10(1): 29-39.

[8] Chen Z T, GUEVARA J A. Systematic selection of very important points (VIP) from digital terrain model for constructing triangular irregular networks[C]. In Auto-carto, 1987, 8, pp. 50-56.

[9] ARYA S, MOUNT D M. Approximate Nearest Neighbor Searching [C], Proc. 4th Annu. ACM-SIAM Sympos. on Discrete Algorithms(SODA’93), 1993, 271-280.

[10] 吴艳兰,胡海,胡鹏,等.数字高程模型误差及其评价的问题综述[J]. 武汉大学学报(信息科学版), 2011, 36(5): 568-574.