改进的GM-AR组合模型在地铁沉降预测中的应用

成 枢，郭祥琳，冯东恒

(山东科技大学 测绘科学与工程学院，山东 青岛 266590)

用于变形预测的方法很多，例如，时间序列、灰色系统、神经网络和卡尔曼滤波等。每种预测方法都有自己的特点[1-3]，如：时间序列分析法可以较好地拟合出序列中的趋势项；灰色模型能通过小样本数据实现对系统运行规律的正确描述。但是，每一种单一方法也有自身的局限性[1,3-4]，如：时间序列模型难以适应随时间和环境而变化的影响因素，进而影响预测的精度；灰色模型对起伏较大的数据拟合精度较低且随着建模序列长度的增加使模型不稳定。在工程实践中，通常选择两种及以上的模型进行组合。国内外学者对组合模型进行了深入的研究，格雷特等[5]把组合方法分为两水平组合方法和通过“合奏”方式进行的组合方法，两种形式的组合方法都相应的提高了预测的精度，但通过“合奏”方式并没有真正避免单一模型所具有的局限性。通过对灰色系统和时间序列组合[6-7]，证明了灰色-时序模型较单一模型的预测精度有了很大提高；通过对灰色模型和神经网络的组合[8]，证明了组合模型能兼顾二者的优点。但这些与灰色模型组成的组合模型都未能避免灰色模型自身因预测长度的增加而使预测精度逐渐降低的弊端。

本文针对灰色系统随着预测的进行，因序列过长使模型不稳定的问题，改进了灰色模型，使得进行建模的序列达到了一个动态平衡的目的。通过灰色系统与时间序列进行模型组合，对地铁沉降作预测，并给出本模型的评价指标。利用已有监测数据建立组合模型，同时对组合模型的效果进行检验与分析。

1 GM-AR组合模型

1.1 灰色GM(1,1)模型

灰色系统[9]由邓聚龙教授于1982年提出，根据灰色系统建立灰色预测模型，对数据下一阶段的变化趋势进行预测。在灰色预测模型中，其核心内容是GM(1,1)预测模型的建立[10]。

(1)

式中：a为发展系数；b为灰色作用量。

随着时间的推进，地表沉降的因素会发生变化[11]，原有预测模型难以适应新变化。由灰色系统的理论可知，倘若在这种情况下仍使用原预测模型，很难保证预测模型的精度和可靠性，为此可用改进的GM(1,1)预测模型进行地铁沉降的预测。

1.2 改进的GM(1,1)模型

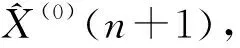
在此基础上再进行预测。

1.3 AR模型

常见的时间序列模型有三种[14]，即AR(自回归)模型、MA(移动平均)模型和ARMA(自回归移动平均)模型，其中AR模型和MA模型是ARMA模型的特殊形式。研究表明，高阶的ARMA模型可由高阶的AR模型来代替[15]，因此本文采用AR模型。AR模型在时刻t的响应Xt仅与其以前时刻的响应Xt-1，Xt-2，…，Xt-n有关，其数学表达式为

Xt=φ1Xt-1+φ2Xt-2+…+φnXt-n+wt.

(2)

式中：ω(i=1,2,…,n)为模型自回归系数；wt为白噪声。

1.4 GM-AR组合预测模型

本文采用灰色GM(1,1)预测模型处理监测数据序列中的趋势项，以此来反应数据序列的发展动向；采用AR预测模型处理监测数据序列中的波动项即对残差序列进行预测；将两者相加作为最终的预测结果。

1)趋势项的确定。对灰色GM(1,1)模型求解可得

(3)

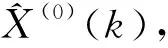
(4)

2)波动项的确定。在采用AR模型对残差序列进行预测时，首先要对残差序列的平稳性进行检验，最常用的检验法为逆序检验法。

设残差序列为e，即

e={e1,e2,…,eM}.

统计量Z为

(5)

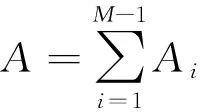
若|Z|<1.96，说明残差序列是平稳的，否则残差序列是非平稳的，需对残差序列进行差分处理，直至残差序列平稳。

其次要为AR模型定阶。本文采用AICC准则对模型的阶数进行判定，即

(6)

由上式计算AR模型对应的AICC值，最终取极小值所对应的p值，此时p值即为AR模型的阶数，进而可得最优模型。

通过对AR(p)模型的计算，可得波动项的值为

(7)

确定趋势项和波动项之后，可根据式(4)和式(7)对地铁站的沉降监测数据建立GM-AR组合预测模型，求得t时刻的预测值xt，即

(8)

2 精度评定

2.1 GM(1,1)预测模型的精度评定

计算后验差比值c和小概率p为

若c和p符合精度要求则说明模型适合监测点的预测，否则修正残差，再一次建模，直至符合要求。其精度指标如表1所示。

表1 灰色预测模型精度等级

2.2 GM-AR预测模型的精度评定

根据建立的组合预测模型，将得到的预测值与实际观测值进行对比，从而确定组合预测模型的精度。评价组合预测模型精度的指标主要有残差、相对误差等。

(9)

(10)

通过式(9)和式(10)计算相应精度指标，即可对GM-AR组合模型的精度进行评定，从而比较模型之间的精度。

3 实例分析与应用

为验证各模型间的预测效果，以某城市地铁建设中地铁站的二等水准精度的观测数据进行实例验证。所选地铁站为地下两层岛式车站，车站主体基坑采用地下连续墙维护结构。车站一侧为居民区；另一侧地面为电力电缆，地下分布着城市供水管道、城市燃气管道和国家电缆等。

本文选取该地铁站J1号45期的观测数据进行应用与分析。通过对所选取观测数据进行建模，研究GM(1，1)模型、GM-AR模型和改进后GM-AR模型的预测精度，讨论何种模型对地铁施工引起的沉降预测更加精确。

3.1 数据的预处理

受施工场地地质、周围环境、天气等因素的影响，每期观测数据的时间间隔不同，而预测模型一般要求观测数据组成的时间序列是等间隔的。因此，首先对观测数据进行预处理。根据该地铁站所处地质条件，并结合相同地质条件下地铁站沉降观测方案，本文采用线性内插法将实际观测到的高程值转化为等间隔的高程观测值数据，预处理后结果见表2。

3.2 模型的建立

1)对J1号选取前30期数据进行GM(1,1)建模，验差评定精度。可得J1号点GM(1,1)模型参数：aJ1=2.794 2×10-6，bJ1=72.965 5，后验差cJ1=0.238 2<0.35，pJ1=1>0.95，根据表1可知该预测模型拟合精度能达到一级。

2)建立模型进行预测，可得残差序列，对残差序列建立AR模型。

对残差序列进行平稳性检验，|ZJ1|=0.785<1.96，说明残差序列是稳定，对该序列建立AR模型；

利用AICC准则对J1号点残差值定阶，由式(6)得J1号点残差值阶数p=8；

对AR模型求参，可得预测值的模型为

eJ1(t)=-0.818 4eJ1(t-1)-0.193 7eJ1(t-2)+

0.305 5eJ1(t-3)+0.006 5eJ1(t-4)+

0.153 8eJ1(t-5)-0.161 3eJ1(t-6)-

0.095 1eJ1(t-7)+0.156 3eJ1(t-8).

3.3 实验分析

分别采用三种方案对原始高程值进行分析求得预测高程值：

方案一：由前30期数据建立GM(1,1)模型，进而预测出后15期高程值；

方案二：用GM(1,1)模型预测出监测点的大致沉降趋势，用AR模型预测出残差的变化趋势，最终通过二者相加求得GM-AR模型的预测值；

方案三：用改进后GM(1,1)模型预测出监测点的大致沉降趋势，即先预测出31～35期高程值，然后利用6～35期数据再次用GM(1,1)模型预测出36～40期数据，以此每预测5期数据更新一下预测模型，最终通过和AR模型预测出的残差值相加求得改进的GM-AR模型的预测值。

通过三种方案的实施，利用式(9)和式(10)可得J1号点各模型的残差值和相对误差。各模型残差和相对误差对比如表2所示；各模型预测结果与原始值对比如图1所示。

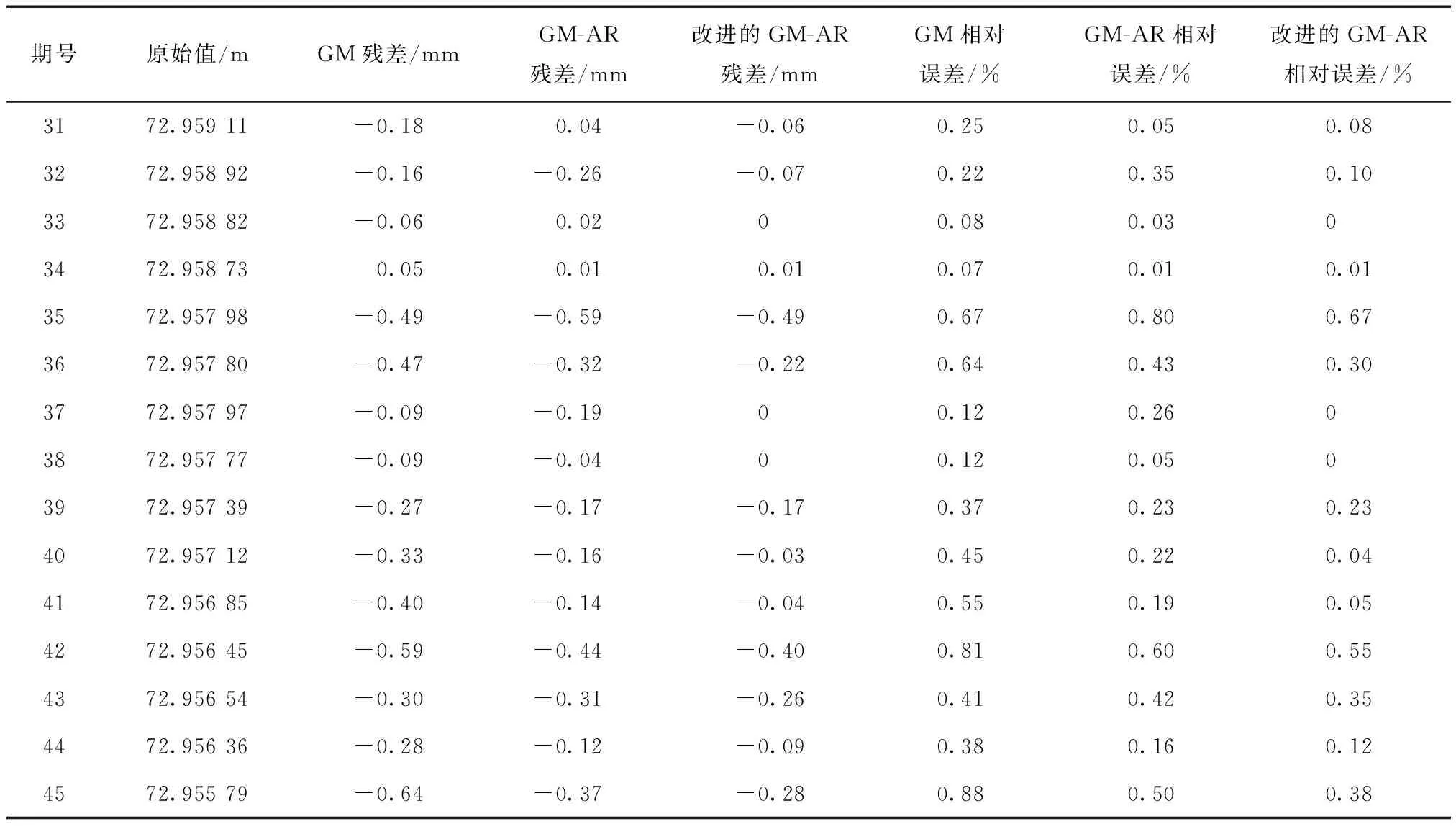
表2 J1号点各模型预测结果数据对比表

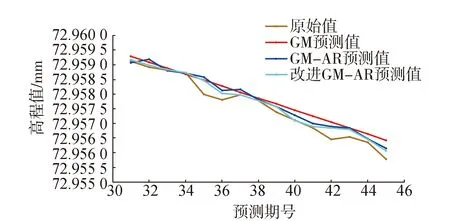
图1 各模型预测结果与原始值对比图

由表2和图1可知，GM(1,1)模型预测结果的相对误差保持在0.22%～0.88%，说明该模型对地铁沉降的预测符合精度要求，但其预测值总体要高于实测值，即该模型能预测出地铁沉降的总体趋势而不能预测出具有随机性的波动项；GM-AR组合模型较好地解决了GM(1,1)模型不能预测波动项的问题，总体误差较GM(1,1)模型提升30%～50%，但对较长期数的预计会产生数据冗余，影响预测的精度；通过改进的GM-AR组合模型，使之成为一个动态的等维GM-AR组合模型，在GM-AR组合模型的基础上使精度再度提升10%～30%，预测效果较好。

4 结束语

本文研究传统GM(1,1)模型、GM-AR组合模型和改进的GM-AR模型在地铁沉降监测中的应用，对地铁站观测站J1号前30期数据建立预测模型，并采用后15期数据进行检验，验证三种模型在地铁沉降预测中的可行性。最终，GM(1,1)模型可以对地铁沉降做整体预测，但无法对波动性的残差进行修正；通过用AR模型对残差值进行修正预测，与GM(1,1)组合模型，使得预测值得到一定程度的改善；在此基础上进行组合模型的改进，避免预测产生冗余数据，使得预测精度得到进一步地提高。

[1] 吴雅,杨叔子,陶建华. 灰色预测与时序预测的探讨[J]. 华南理工大学学报,1988,16(3):27-33.

[2] 徐秀杰,黄张裕,凌晨阳,等. 基于小波分析的灰色组合模型在变形监测数据处理中的应用[J].工程勘察,2014(4):80-83.

[3] 潘国荣,谷川. 形变监测数据组合预测[J]. 大地测量与地球动力学,2006,26(4):27-29.

[4] 王强,戴晟晖. 灰色理论与时序模型的发动机状态监测分析[J]. 计算机工程与应用,2009,45(8):246-248.

[5] [美]格雷特,李洪成. 时间序列预测实践教程[M]. 北京：清华出版社,2012:38-40.

[6] 单锐,王淑花,高东莲,等. 基于时间序列模型与灰色模型的组合预测模型的研究[J]. 燕山大学学报,2012,36(1):79-83.

[7] 刘燕芳,陈启华,丁林磊. 灰色组合模型在变形监测中的应用[J]. 工程勘察,2013(1):58-60.

[8] 王忠桃. 灰色预测模型相关技术研究[D].西安：西南交通大学,2008.

[9] 邓聚龙. 灰理论基础[M]. 武汉:华中科技大学出版社,2002.

[10] 邓聚龙. 灰色系统基本方法:汉英对照[M].2版.武汉：华中科技大学出版社, 2005:35-36.

[11] CHOU W I,BOBET A. Predictions of ground deformations in shallow tunnels in clay[J]. Tunnelling and Underground Space Technology,2002,27(1):3-19.

[12] 袁景竣,钟珞,江琼,等. 新陈代谢GM(1,1)建模与应用[J]. 武汉理工大学学报(信息与管理工程版)，2005(2):168-170

[13] 潘华志,卫建东,夏志国,等. 动态灰色模型在变形预测中的应用[J]. 测绘科学,2007,27(4):121-124.

[14] 王振龙. 时间序列分析[M]. 北京:中国统计出版社,2000.

[15] 杨叔子,吴雅,轩建平. 时间序列分析的工程应用[M].2版.武汉:华中科技大学出版社,2007:1-19.