基于多策略的整数数列学习
杨亚琴,蔡东风,白 宇(沈阳航空航天大学 人机智能研究中心,沈阳 110136)
整数数列学习(Integer Sequence Learning,ISL )是指给定某整数数列的前n项,来学习或发现该数列的规律或通项公式,或预测其后续项数值的过程。很多组合数学和数论问题都涉及或可转化为ISL问题。例如,n皇后解的计数问题、素数公式的发现问题等。ISL也经常出现在数学竞赛中,例如:1986年第四届美国数学邀请赛[1]中,给出数列的前7项求数列的第100项是多少。ISL具有挑战性,适合采用数学和机器学习相结合的方法来求解。
2016年,国际著名的大数据竞赛平台Kaggle[2]举办了整数数列学习竞赛。该竞赛任务的数据集主要来源于OEIS[3](The On-Line Encyclopedia of Integer Sequences)网站。数据集共包括227 690个整数数列,分为训练集和测试集,其中测试集数列的最后一项被去掉。任务要求仅利用训练集对测试集中整数数列的被去掉的最后1项进行预测。该竞赛促进了ISL的普及与发展,提出了一些有效的预测方法。本文针对Kaggel平台竞赛任务分析已有方法的特点,提出了一种基于多策略的ISL方法,取得了良好的预测效果。
1 相关研究
对于ISL任务,kaggle的ISL竞赛参赛者给出了一些有效的预测方法。Nina Chen[4]利用线性递推公式来表达数列。把公式按照阶数分为二阶线性递推、三阶线性递推、四阶线性递推等三类,并分别采用待定系数法进行求解。该公式发现方法能较好地解决低阶具有线性递推公式数列的预测问题,但是求解范围较小(仅限低阶线性递推公式)。
EndIn Tears[5]提出了利用回归模型来学习整数数列。首先构建线性回归模型并求解;再制定误差阀值判断求解是否成功;若求解失败则利用更复杂的非线性模型进行预测。相比于Nina Chen的低阶线性递推来说,它不仅可以求解非线性递推公式,而且对递推公式的阶数没有限制。
Nina Chen[6]还通过发现使用学习数列和已知数列间线性关系的方法实现整数数列的学习。首先使用签名对数列进行标记,对于相同标记的学习数列和已知数列求其线性关系。然后再利用该关系和已知数列对学习数列进行预测。
文献[7]提出基于马尔科夫链构建整数数列模型。把整数数列当成马尔科夫链预测整数数列的下一项任务也就是预测马尔科夫链的下一个元素。此外,文献[8]提出了使用N元语法预测整数数列。实验说明机器学习的方法对整数数列预测问题是有效的。
文献[9]提出一种面向计数问题的公式发现方法,采用svm算法对整数数列进行分类,然后求解数列的递推公式。发现了部分新公式,取得了很好的效果,但公式类型和求解算法还可进一步扩充和优化。
文献[10]提出利用后缀表示法表示一个公式的方法,并把求解数列公式问题转化为固定空间的搜索问题。但是求解空间相对固定,因此可求数列比较局限。
另外,也有一些具有整数数列学习功能的软件工具。最著名的是Wolfram公司开发的数学软件Mathematic[11],其提供的FindSequenceFunction函数可以求解部分整数数列公式并得到广泛应用。此外,Wolfram公司开发的浏览器WolframAlpha[12]也具有数列的分析功能。Mathematic工具包RATE[13]已经应用于整数数列百科全书网站。
2 基于多策略的ISL方法
2.1 定义
定义1 整数数列:整数的任意有序集,这些整数称为数列的项或元素,用an来表示数列的第n项,用{an}表示整数数列,以下简称数列。用|{an}|来表示数列{an}的长度。
定义2 数列的差分:数列相邻项的差称为数列的差分。对于任意数列{an}={a1,a2,…},其差分算子符号Δ定义如下:Δa1=a2-a1,
Δa2=a3-a2,一般地对于任意n有Δan=an+1-an,数列{an}的差分数列为{Δan}={a2-a1,a3-a2,…},|{Δan}|=|{an}|-1。
定义3 数列间的线性关系:若数列{an}与数列{bn}满足公式c0*an+c1*bn+i=K(其中,c0,c1,K,i为整数),称数列{an}和数列{bn}之间存在线性关系。若i不为0又称移位线性关系。例如:已知
{an}={17,33,41,57,65,73,89,97,105,113}
{bn}={1,3,4,6,7,8,10,11,12,13
且an-8bn=9 (n=1,2,…,10)
因此{an}与{bn}满足线性关系。
再如: {an}={1,2,3,4,5,6,7,8,9,10}
{bn}={1,2,3,4,5,6,7,8,9,10}
且an-bn+1=-1 (n=1,2,…,10)
因此{an}与{bn}满足移位线性关系。
2.2 算法框图
通过对已有ISL方法分析,我们把通过发现公式后再预测的方法统称为公式发现法,简称公式法;把通过发现与训练集中数列的关联关系来预测的方法统称为关联实例方法,简称关联法;另外还有基于n元文法、基于马尔科夫模型等方法,统称为基于机器学习的方法。
公式法是当前已知ISL中最有效的方法,具有较高的召回率和正确率。但是,对于比较复杂的数列,很难发现或不一定存在公式表达。而关联法试图通过发现测试数列和已知数列之间的函数关系来预测后续项值。关联法的关键是如何能从已知数列或训练集中高效地发现关联数列。由此可见,公式法和关联法二者具有很好的互补性,有些类似于机器学习方法中的基于模型的方法和基于实例的方法的不同和互补关系。
基于机器学习的预测方法的突出特点是对于任何测试数列都会给出一个预测结果。但是,目前已有方法的预测效果还不够理想。但当公式法和关联法得不到答案时,可作为一个很好的补充。本文尝试采用神经网络方法进行预测,提出了基于RNN模型的预测方法,取得了良好的效果,简称神经网络法。
依据以上分析,为实现各种方法的优势互补,本文提出了一种基于多策略的ISL方法。该方法首先利用公式法求解测试数列公式,若求解成功则利用公式进行预测,并返回结果结束;若求解失败则利用关联法求解测试数列与已知数列间关系,若求解成功则利用关联关系进行预测,并返回结果结束;否则利用神经网络法对测试数列进行预测,返回预测结果并结束。算法框图如图1所示。
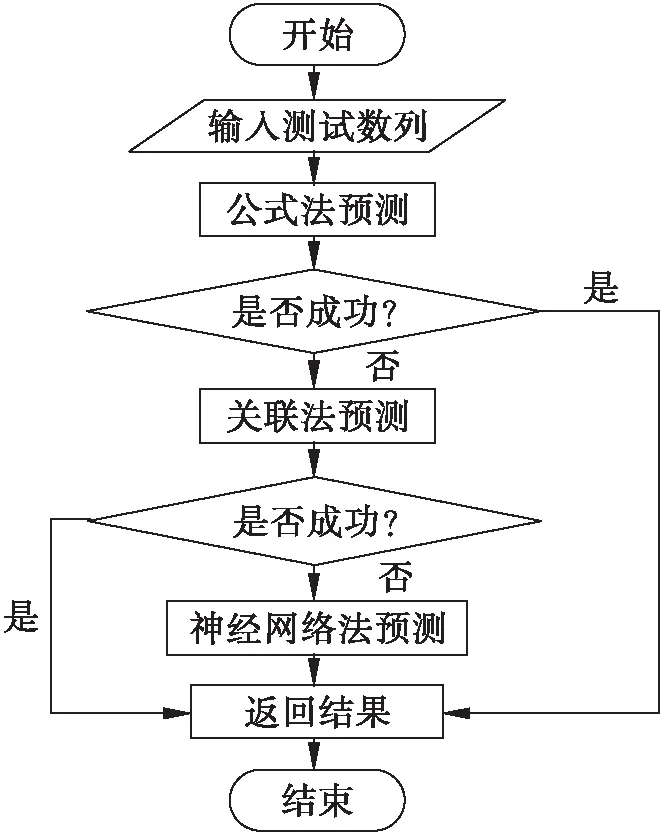
图1 系统框图
2.3 公式法
公式法是ISL最重要和有效的方法。该方法利用数列公式进行整数数列学习。递推公式是一种利用数列各项间的关系来表达数列的公式,具有容易理解、表达范围广泛等优点。因此本文采用递推公式来表示数列。一般形式如式(1)所示。
(1)
其中m为递推公式的阶数,bi,ci,di为递推公式的参数。从公式(1)可见,本文提出的公式法不仅包括线性递推公式(bi,ci全部等于0时),还包括非线性递推公式,同时考虑到参数不易过多,将递推项的系数多项式取为2次。当给定测试数列时,可由公式(1)构建线性方程组,求解公式中bi,ci,di参数。
上述求解参数方法可能会出现过拟合现象。为避免过拟合将测试数列数据分为求解数据和验证数据,利用求解数据来求解公式,再利用验证数据来验证公式是否正确,即采用“求解+验证”的方法。若验证数据全部满足求解到的公式则认为公式求解成功,否则求解失败。公式法流程图如图2所示。
例如:{an}={1,4,10,23,53,123,286,665,1546}
求解数据:{1,4,10,23,53,123,286} (n=1,2,…7)
验证数据:{665,1546} (n=8,9)
公式求解:an-2an+1+3an+2-an+3=0
公式验证:a5-2a6+3a7-a8=0
a6-2a7+3a8-a9=0
因此公式求解成功
预测:a10=3a9-2a8+a7=3 594
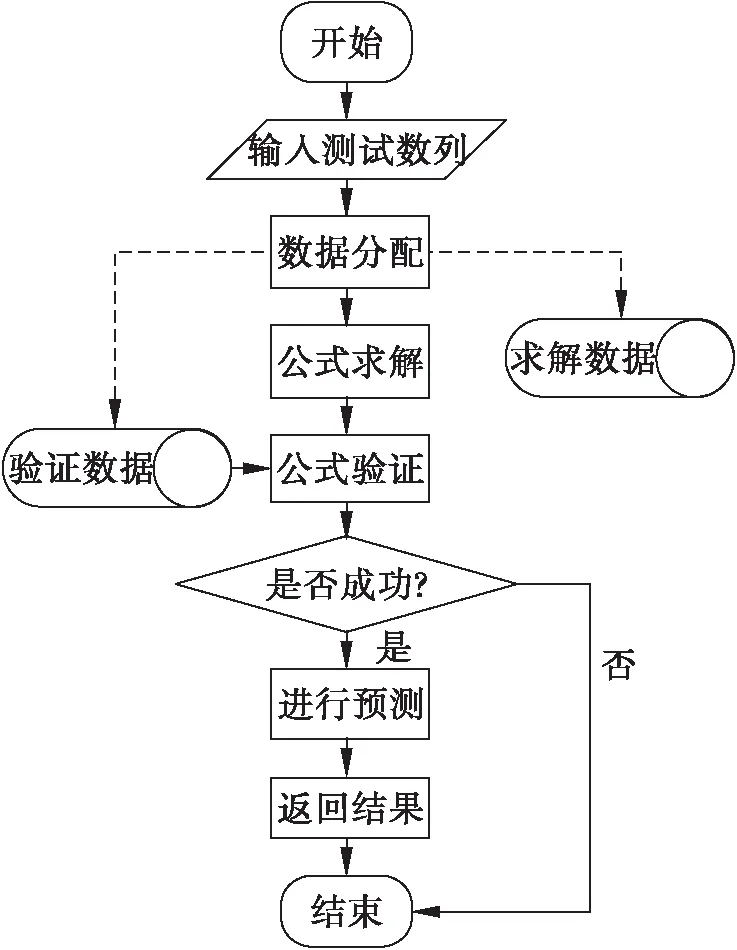
图2 公式法流程图
2.4 关联法
公式法虽然可准确地预测存在公式的数列,但对于不存在公式或者不易求解的数列并不适用。关联法利用数列间的关系进行整数数列学习,可以弥补公式法的这一不足。
当训练实例数量较多时,如果直接利用测试数列匹配所有训练实例求解关联关系,需用较长时间。所以本文先抽取特征进行关系判别,如果存在关系则进行求解。关联法流程图如图3所示。
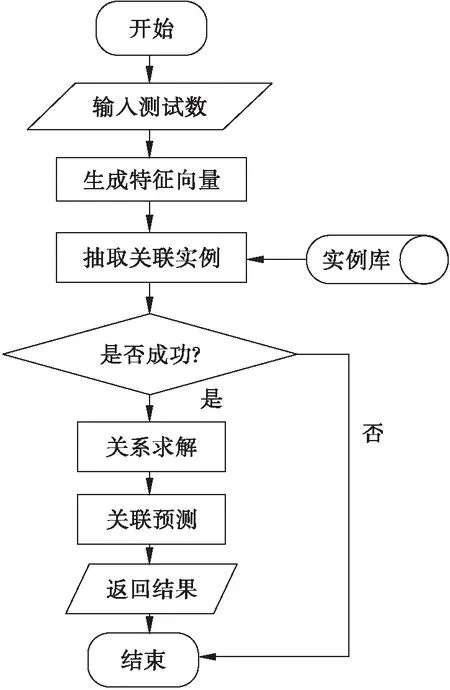
图3 关联法流程图
数列间的关联关系可能多种多样,本文重点研究了两个数列间的线性关系和移位线性关系。相比于Nina Chen的线性关系方法,增加了移位处理,表达范围更广。
为了能快速从实例库中找到关联实例,根据线性关系的特点,引入数列的特征向量X的概念[6],计算公式如式(2)所示。
(2)
其中sign为符号函数,GCD为求公约数函数。
可以证明,当具有相同长度的两个数列的特征向量相同时,它们之间一定存在线性关系。
实例库中存放着训练集数列和每个数列对应的特征向量(按特征向量排序)。当给定一个测试数列时,首先求其特征向量,然后在实例库中查找关联实例,使实例的特征向量包含该测试数列的特征向量,如果存在这样的关联实例则求解关联关系,并利用该关系进行预测。
例如:
{an}={1021,1031,1033,1051,1061,1063}
{bn}={5,10,11,20,25,26,38,39}
X({an})={5,1,9,5,1}
X({bn})={5,1,9,5,1,12,1}
因此{an}、{bn}满足线性关系。
求得an=2bn+1011
预测出a7=2b7+1011=1087
关联法的效果主要取决于训练实例库的规模大小和可快速求解的关联关系的类别数量,是一种基于实例的有效方法。
3 神经网络法
公式法和关联法可准确地对存在公式或关系的数列进行预测。但对于不存在公式且找不到关联实例的数列并不能得出结果。对此,本文提出一种基于循环神经网络(RNN)[14]的数列预测方法。
RNN的目的就是用来处理序列数据。一般的前馈神经网络是从输入层到隐含层再到输出层,层与层之间是全连接的,每层之间的节点是无连接的,没有任何记忆能力,不适合处理序列问题。而RNN通过对每一时刻隐含层输出状态的记忆和反馈循环实现了序列间的关联计算。
图4是RNN的基本原理示意图以及RNN网络按时间顺序的展开示意图。其中xt、ot、st分别表示在t时刻网络的输入、输出和中间隐含层的输出,而U、V、W分别是输入、输出和反馈的参数矩阵。RNN的主要特点是具有记忆功能,t-1时刻隐含层的输出st-1会被反馈回来,作为t时刻的输入部分,即:
st=f(U*xt+W*st-1)
RNN已被成功地用于自然语言处理任务,如词向量表达、汉语分词、词性标注、机器翻译等。本文的整数序列预测问题是一个典型的数字序列处理问题,有些类似于语言处理中的词预测,因此也适合用RNN来处理。
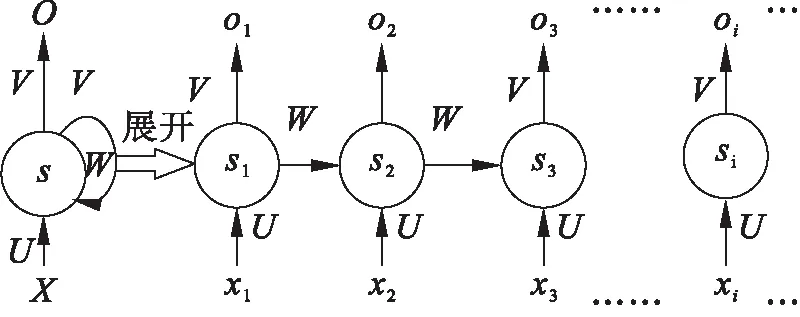
图4 RNN原理示意图
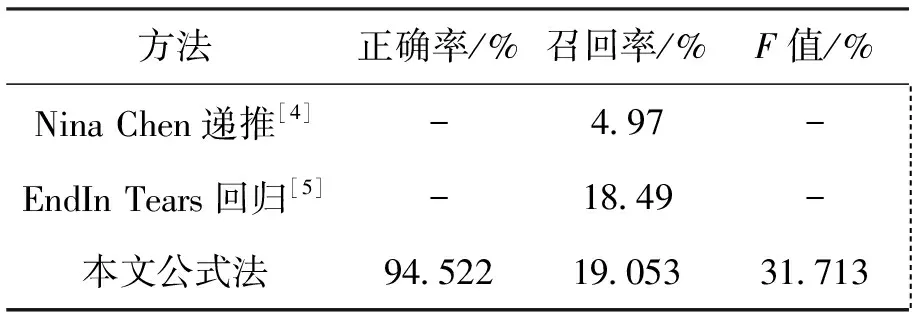
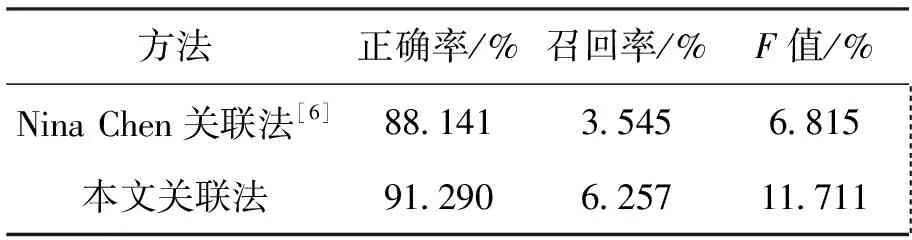
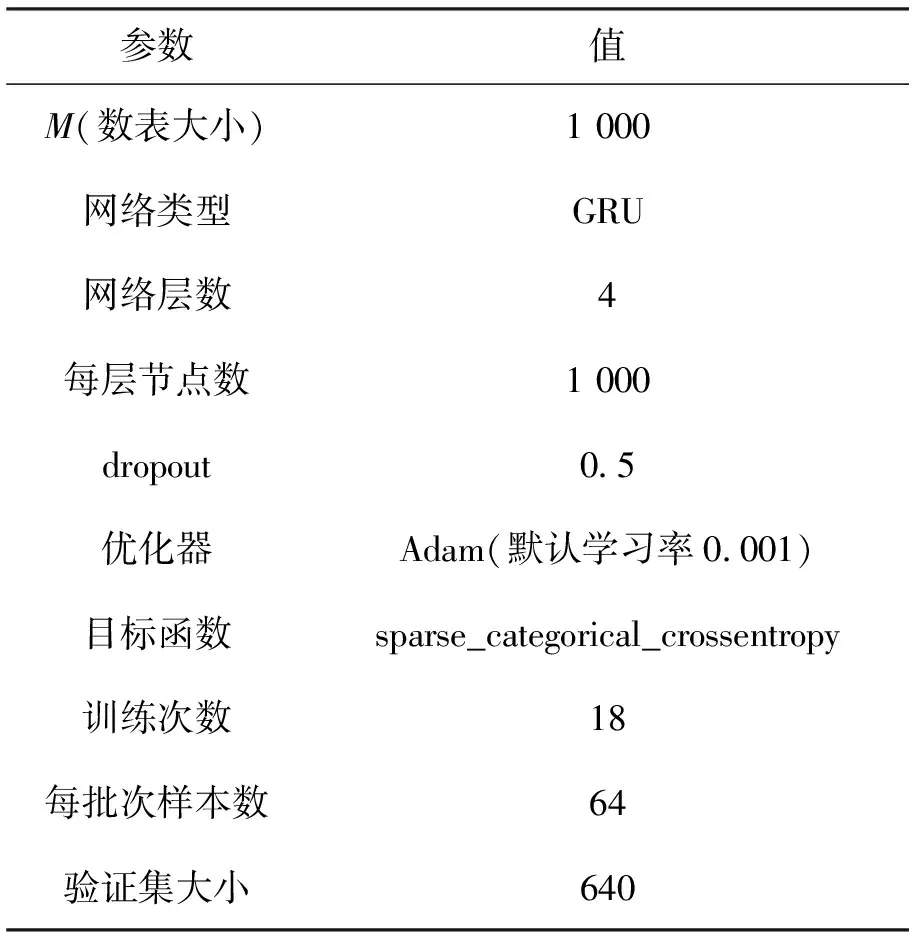
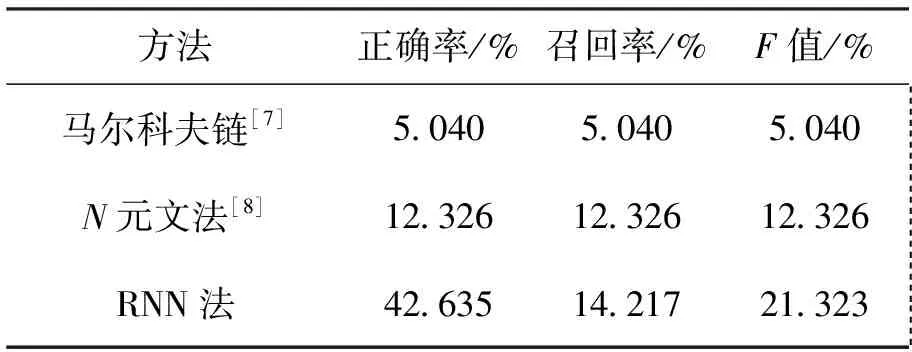
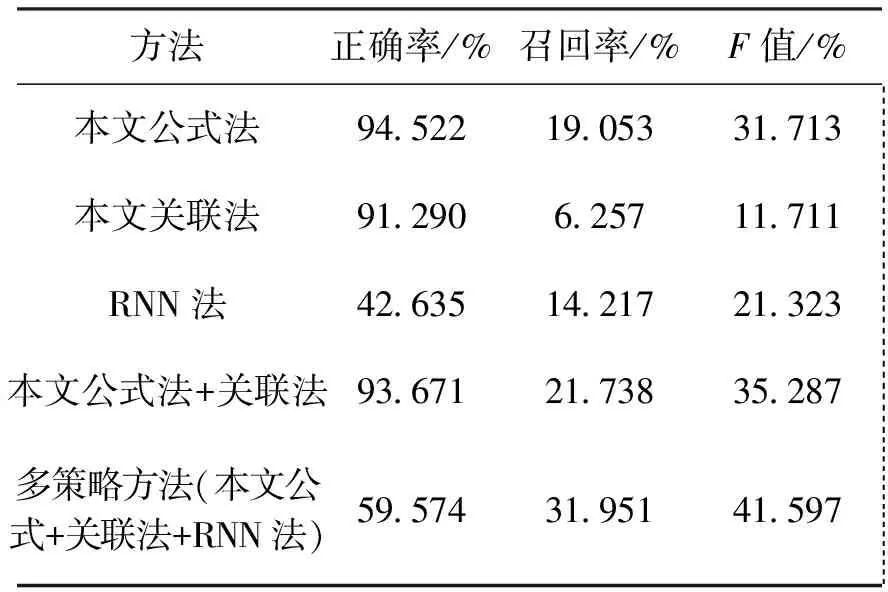
整数数列中有些数的数值很大,如果将整个区间的整数都保存在数表中,势必造成数表很长和数据严重稀疏问题。为此,本文设定数表大小为M,将数值大于M的数都映射为符号“O”,只对an 图5 循环神经网络流程图 相对于N元文法[8]和马尔科夫链预测方法[7],由于本文提出的基于循环神经网络的预测方法充分利用了循环神经网络模型处理序列数据的特长,显示出了明显的优势,取得了更好的实验结果(见4.2.3节)。 作为实验数据,本文采用Kaggle整数数列学习竞赛的数据集,其主要来源于著名的整数数列百科全书OEIS网站。该数据集共有整数数列227690个,分为113845个训练数据和113845个测试数据。任务要求仅利用训练集对测试集中整数数列的最后1项进行预测。 OEIS是一个在线整数数列百科全书,它由Neil J.A.Sloane 在 1964 年创建,目前已容纳超过二十九万多个数列。OEIS 对每一个数列都有详细表述,包括:数列的来源、数列的相关文献、已发现的数列公式、生成数列的程序、求解数列的难易程度等,是公认的研究整数数列问题的重要公开资源。 正确预测一个整数数列的后一位数值是指预测结果和答案数值完全相同。尽管Kaggel竞赛中只对召回率进行评价,但本文认为正确率对预测结果也非常重要,应该同时考虑。所以实验采用了召回率、正确率和F值作为综合评价指标,计算公式如式(3)~(5)所示。 (3) (4) (5) 4.2.1 公式法对比实验 公式法通过求解整数数列公式来进行预测。如果能找到通用公式,一般预测的正确率都比较高,特别是当给定预测数列较长时效果会更好。但也会出现过拟合或有多个公式作为候选的选择问题。表1是本文公式法与已有类似方法的比较实验结果。 表1 公式法对比实验结果 由表1可见,本文的公式法相比于Nina Chen的线性递推方法[4]和EndIn Tears回归方法[5]更有效。召回率提高的同时,正确率达到了94.5%(其它方法只有召回率的数据)。 表2列出了本文公式法求解发现的部分公式。针对测试集的前50个测试数列共发现了9个递推公式。其中4个是OEIS库已有,5个为新发现的公式。新发现公式中,既有高阶的线性递推公式也有非线性递推公式。 表2 递推公式展示 注:表中编号为整个数据集的数列编号,在测试集中并不连号。 4.2.2 关联法实验结果 关联法是试图发现数列间的关联关系,利用该关系和已有数据对未知数据进行预测。目前本文实现了对线性关系和移位线性关系的快速发现和求解。 表3是关联法的比较实验结果。与Nina Chen关联法相比,由于本文方法不仅能发现线 性关系(非移位),还能发现移位线性关系,所以召回率得到较大提升。 表3 关联法对比实验结果 4.2.3 神经网络法实验结果 循环神经网络法是首先构建RNN数列预测模型,然后利用该模型进行预测,实现了数值大小在M以内的数值预测。 本文使用深度学习框架keras搭建GRU网络进行整数数列模型训练。近年来有很多RNN的改良网络被提出,比较流行的为长短记忆网络LSTM(Long Short Term)和门限循环网络GRU(Gated Rucurrent Unit)[15]。GRU是由Cho,et al在2014年首次提出,是LSTM的简单变体。LSTM和GRU都能通过各种门将重要特征保留,保证其在长距离传播的时候也不会被丢失。在训练效果上,它们差别不大。相比于LSTM,GRU的结构简单、训练和预测时间少[16]。故本文采用GRU网络进行训练。网络参数如表4所示。 表5为机器学习方法对比实验结果。相比于马尔科夫链方法[7]和N元文法方法[8],循环神经网络的方法发挥了其处理序列数据的优势,自动学习数列特征,召回率提升的同时, 正确率也得到了显著提升。 表4 循环神经网络参数设置 注:参数M代表前边提到的数表的大小(见3节)。 表5 机器学习法对比实验结果 4.2.4 多策略方法实验结果 如前所述,本文进一步将公式法、关联法和RNN方法进行融合,提出了基于多策略的预测方法,希望能实现各方法之间的优势互补。表6是相关实验结果。 表6 多策略整数数列学习实验结果 从表6可见,单一方法中公式法效果最好,选作为本实验的比较基准。首先,将关联法与公式法结合,召回率和F值分别提升了2.68(19.05% ->21.73%)和3.57(31.71%->35.28%)个百分点,取得了较好效果;再进一步融合RNN法,即形成本文的多策略方法,召回率和F值获得了更显著的提升,分别提升了12.9(19.05% ->31.95%)和9.88(31.71%->41.59%)个百分点。由此可见,多策略的方法确实实现了优势互补,显著地提升了预测效果。 最后,需要说明一下本文为什么没有直接拿ISL竞赛结果进行比较。Kaggle举办的ISL竞赛中,由于测试集的答案在OEIS网站上几乎都可找到,尽管组织方宣布了不可参考,但还是有一些人参考了,使得最终发表的评测结果失去了客观性和可比性。关于这一点,Kaggle在网站上发布了一份公告:“最近在这场比赛中涌现出不切实际的成绩。 如果你的分数(召回率)远高于0.3,你应该问自己,你是否违反了规则。”[17] 针对整数数列学习问题,本文将已有方法划分为公式法、关联法和机器学习法,并对已有公式法和关联法进行了改进,此外还提出了基于循环神经网络的机器学习方法,融合上述三种方法,提出了一种基于多策略的整数数列学习方法。在2016年Kaggle举办的整数数列学习竞赛公开测试集上进行实验,取得了良好的实验结果,多策略方法的召回率和正确率分别达到31.95%、59.57%。 进一步工作将重点开展以下研究: (1)扩展可求解的公式类型。目前公式法只能求解递推公式,但并不是所有的数列都存在递推公式。 (2)扩展可求解的关联关系。目前关联法只考虑了线性关系,希望扩展更多的关系类型。关键的问题是找到快速求解的方法。 (3)扩展循环神经网络可求解的数据范围。为了防止数据稀疏,目前的方法将数表控制在1 000以内,对于很多快速增长的数列不能求解,这是一个比较困难的问题。 (4)探索更有效的学习方法和融合方法,发现更多的未知的数列规律。 参考文献(References): [1] 佩捷.历届美国数学邀请赛试题集[M].哈尔滨:哈尔滨工业大学出版社,2013. [2] BLUM A,HARDT M.The Ladder:a reliable leaderboard for machine learning competitions[J].Eprint Arxiv,2015:1006-1014. [3] SLOANE N J A.The on-line encyclopedia of integer sequences[C].Symposium on Towards Mechanized Mathematical Assistants International Conference,Springer-Verlag,2007:130. [4] NINA C.Recurrence relation[EB/OL].https://www.kaggle.com/ncchen/recurrence-relation.下载时间:2017-10-20. [5]TEARS E.Integer sequence learning-moving up the leaderboard[EB/OL].http://www.diaryofakaggler.com/2016/integer-sequence-learning-moving-up-the-leaderboard.下载时间: 2017-11-14. [6] NINA C.Match test set to training set[EB/OL].https://www.kaggle.com/ncchen/match-test- set- to-training-set.下载时间:2017-11- 14. [7] HERRERO E P.Predict OEIS with markov chains[EB/OL].https://www.kaggle.com/enrique1500/predict-oeis-with-markov-chains.下载时间:2017-11-14. [8] HERRERO E P.OEIS ngram exploration[EB/OL].https://www.kaggle.com/enrique1500/oeis-ngram-exploration.下载时间:2017-11-14. [9] 蔡东风,朱耀辉,白宇.一种面向计数问题的公式发现方法[J].沈阳航空航天大学学报,2016,33(5):61-67. [10]S ARTUR.Formula analyzer:find the formula by parameters[EB/OL].www.figshare.com,下载时间:2017-11-14. [11]王福贵,王晓玲.Mathematica及其数学应用[M].北京:中国农业出版社,2013. [12]LANG A.Teaching calculus with wolfram|Alpha[J].International Journal of Mathematical Education in Science & Technology,2010,41(8):1061-1071. [13]KRATTENTHALER C.Advanced determinant calculus[M]//The Andrews Festschrift.Heidelberg:Springer,2005. [14]ZAREMBA W,SUTSKEVER I,VINYALS O.Recurrent neural network regularization[J].Eprint Arxiv,2014:1-8. [15]FU R,ZHANG Z,LI L.Using LSTM and GRU neural network methods for traffic flow prediction[C]//Chinese Association of Automation.IEEE,chengdu,2017:324-328. [16]CUKIERSKI W.Please do not cheat[EB/OL].https://www.kaggle.com/c/integer-sequence-learning/discussion/23816.下载时间:2017-11-14.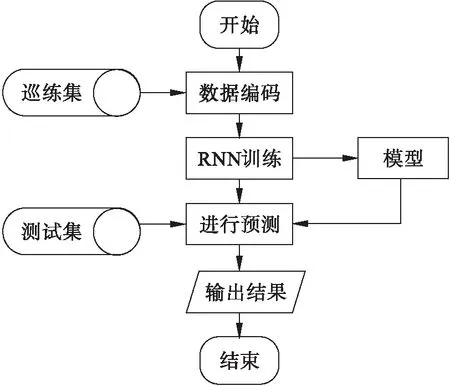
4 实验
4.1 评价标准



4.2 实验结果的分析和比较

5 结论

