基于遗传优化岭回归的GM(2,1)供应链风险预测

赵 川，揭海华，杨浩雄

（北京工商大学 商学院，北京 100048）

0 引言

近年来，在全球化的经济商务环境中，供应链与供应链之间的竞争逐渐替代企业竞争成为经济社会前进的原动力。供应链中各个环节之间的合作，会由于信息传递偏差，信息共享不充分，市场不确定因素以及政治大背景、经济形式、法律等因素产生各种风险[1-4]。因此，关于供应链风险的预警研究显得极为重要。有学者应用灰色预测模型GM(2,1)对供应链风险进行预测，该方法可以用较少的数据序列反映系统主要动态特性,且能够对于供应链风险预测模型进行拟合[5]。文献[6]指出在求解灰色预测模型GM(2,1)的过程中，数据的累加和累减会使得灰微分方程呈现出很强的病态性，很难估计出合理的参数，并提出通过对原始序列和累积法对GM(2,1)进行数乘变换以降低其病态性。文献[7]考虑了一种基于微粒群算法的GM(2,1)扩展优化模型GM(2'1'λ'ρ)，在GM(2,1)的基础上通过引入参数λ,ρ并利用微粒群算法对参数λ'ρ进行优化得到模型GM(2'1'λ'ρ)，拓展了灰色预测模型的应用范围，提高了预测精度。本文在求解灰色系统模型的过程中，将岭回归参数引入到灰微分方程中，较好地消除了变量间共线性的影响,解决了病态性问题。进一步地，本文还利用遗传算法在全域内搜索岭参数k并获得了较优的岭回归模型。

1 GM（2,1）预测模型

GM(2,1)是针对系统模型不明确性，信息不完整性，借由预测及决策方法来进行系统关联分析的模型[8]。GM(2,1)灰色预测模型的建模过程可简化为以下四步：

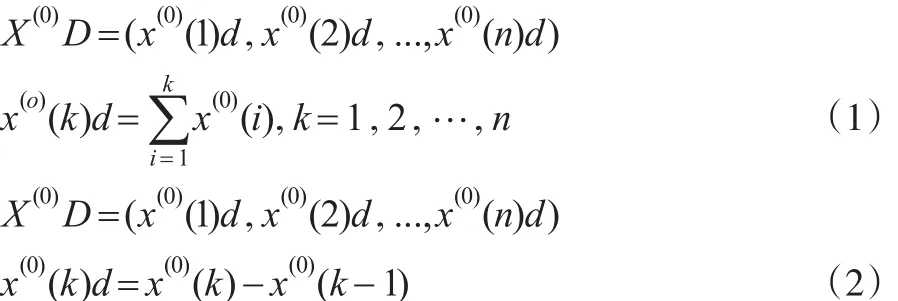
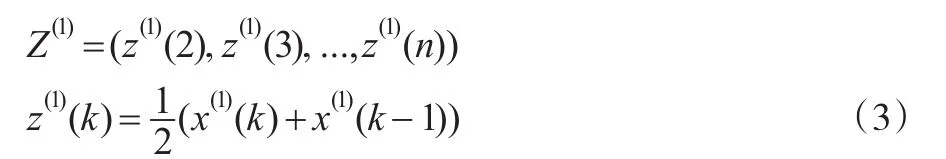
(2)构造矩阵 B*β=Y ，其中：

(3)构建GM(2,1)模型的白化方程：

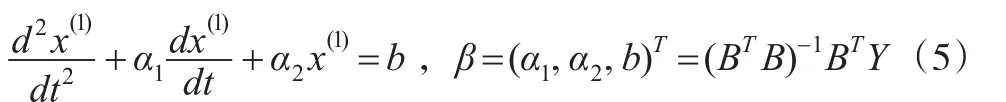
(4)预测与误差检验：

求解预测微分方程，得出预测累加值，通过还原，得到预测序列。根据相对误差和平均误差公式：

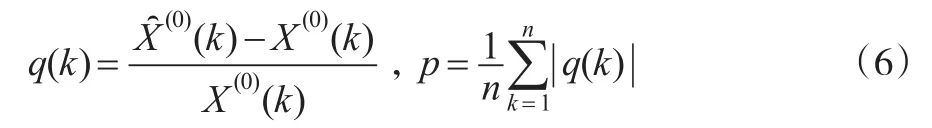
以及关联度公式：

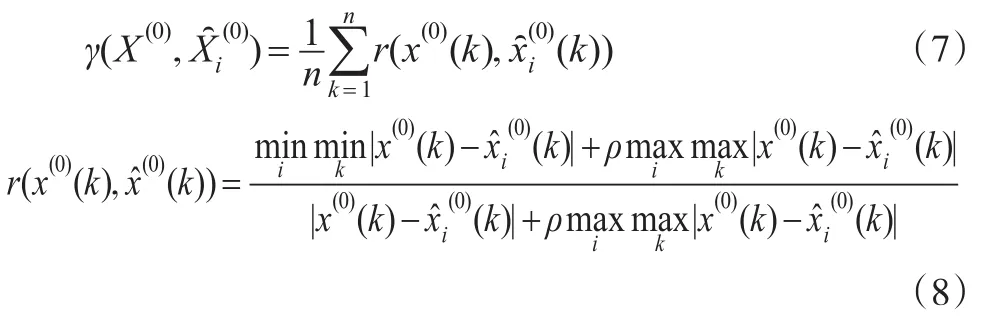
计算预测序列误差和关联度并与原序列进行比较，判断模型效果。根据经验，当ρ=0.5时，关联度大于0.6，符合要求[9]。

2 遗传优化岭回归灰色预测模型

2.1 岭回归

岭回归分析是一种改良的最小二乘分析方法，是一种专门用于共线性数据分析的有偏估计回归方法。该方法通过将XTX+KI代替方程中的XTX，人为地把最小特征根由minλi提高到min(λi+k)，这样有助于降低均方误差[10，11]。这时 β 的岭估计定义为：

当k取0时即为通常所说的最小二乘估计，当k不为0时即为岭回归估计，一般情况下，k取0到1之间的数值。岭回归模型在相关矩阵中引入很小的一个岭参数k值，通过将它与主对角线元素相加来降低参数的最小二乘估计中复共线特征向量的影响[12]。

2.2 遗传算法中正则化方程的选择

本文主要采用遗传算法确定最优的岭参数k值，选定Tikhonov正则化泛函作为遗传算法的适应度函数，在搜索空间内，取达到适应度函数值最小时得到的正则化参数值为最优的岭参数k值。

在进行幼龄果树修剪时，由于修剪对局部涨势有促进作用，所以一般情况下不适宜修剪过重，避免影响到果树营养生长和花芽的正常形成。主要采用轻修剪措施，适当保留枝条，促进枝条健壮生长，逐步扩大树冠，增加叶量和有效短枝数量为丰产奠定坚实基础。在修剪过程中，可以利用骨干枝以外的部分枝条，通过开拉角度、环剥、环割或摘心、扭梢处理，抑制其旺盛生长，促进果树开花结果。

对于病态方程：B*β=Y，其中B是无穷维Hilbert空间Z到U的线性紧算子，通常右端的观测数据Y不可避免地带有一定的误差δ，即‖Y- Yδ‖≤δ。当算子B条件数很大时，右端项微小扰动都会造成解的失真。如果对原问题的极小化元加上进一步的限制，则可保证极小化元的存在与唯一性。因此必须在目标函数‖Bβ - Yδ‖上加上惩罚项，使新目标函数的求解为适定问题，或者使得极小元满足的方程是一个第二类积分方程。具体说来，对有界线性算子B:Y→β 的极小化Tikhonov泛函 f(k)=‖Bβk-Y ‖2+k‖βk‖2。其中k称为正则化参数，同时也是岭回归参数k。

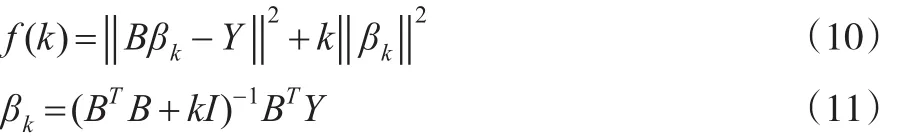
式（10）、式（11）中，B为自变量矩阵；βk为待估参数；Y因变量矩阵。

（3）随机产生初始种群。

（4）设定二进制编码位数、种群大小、进化代数、交叉概率和变异概率。

（5）基于不同的岭参数k，根据岭回归算法计算岭估计参数βk。并通过Tikhonov正则化泛函公式求得适应度函数值 f(k)。

（6）确定遗传算子。选择算子、交叉算子和变异算子。

（7）通过遗传算法搜索最优岭参数k。

（8）将k代入岭回归算法计算岭估计参数βk。

2.3 遗传算法优化的岭回归预测

遗传算法优化的岭回归预测方法是一种在灰色预测的基础上加入由遗传算法全域搜索岭参数的方法，其基本步骤为：

（1）选择编码方式。利用遗传算法优化岭参数k，将岭参数k作为遗传算法优化方程的决策变量，采用二进制编码，范围设定为k∈(0'150)。

（2）确定一个适应度函数。采用正则化原理推导获得岭回归的估计准则作为遗传算法的适应度函数：

3 供应链风险预测

3.1 供应链风险数据的选择与处理

本文选用某连锁零售企业的风险数据作为数值算例验证遗传优化岭回归的GM(2,1)算法在供应链风险预警领域的适用性。首先邀请10位专家分别隔离对该连锁零售供应链配送环节的风险指标进行打分，小于0.2意为风险程度非常低，[0.2，0.4）意为较低，[0.4～0.6）意为中等，[0.6,0.8）意为较高，0.8以上意为风险非常高。将10位专家打分后得到的数据进行均值处理，得到该连锁零售企业配送供应链7期的风险数值。为方便计算，本文将风险均值数据扩大百倍并取对数，得到基本实验数据，见下页表1。

表1 风险均值数据

3.2 预测结果

将该组数据作为灰色预测模型的实验数据，套用GM(2,1)模型进行预测，计算所得微分方程系数矩阵的条件数为1066.6，可以判断该微分方程是严重病态矩阵。将岭回归算法引入GM(2,1)模型以便降低其病态性，并通过遗传算法确定岭回归参数为149.846。应用本文提出的遗传优化岭回归GM(2,1)预测该数据序列,得到的结果为：X̂′=[3.7887 3.9299 3.9234 3.9076 3.8824 3.8479 3.8042 3.7514]，遗传算法结果如图1所示。

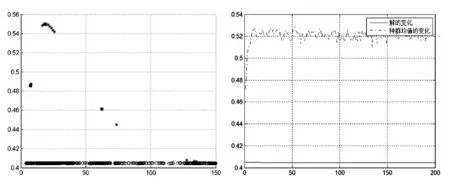
图1 遗传算法结果图

经本文提出的遗传优化岭回归的GM(2,1)算法预测得到的数值算例中供应链配送风险值为0.4258，可以判断出该供应链配送环节在下一年风险发生概率较低且运行良好。本文提出的遗传优化岭回归GM(2,1)算法能够降低GM(2,1)中原始数据微分方程的病态性，有效的估计出岭回归参数，从而能够更加精确的预测出供应链风险值。

从预测结果与实际数据的偏差来看，该模型残差均控制在0.08以内，相对误差控制在3%以内，如表2所示。预测数据的精度较高，灰色预测值参考值基本吻合。从预测结果与实际数据的关联度分析来看，灰色关联度比较表中预测数据与实际数据的关联度接近1，说明预测数据曲线的发展态势与实际情况相接近，如表3所示。

表2 误差分析表

表3 灰色关联度分析

4 结束语

本文针对GM(2,1)预测模型中灰色微分方程的病态性问题，将岭回归参数引入到模型中。同时为了岭回归模型的逼近程度和稳定性达到相对平衡，本文加入了遗传算法求解了最优岭参数k值，其中选定Tikhonov正则化泛函作为遗传算法的适应度函数，并在搜索空间内取达到适应度函数值最小时得到的参数值为最优的岭参数k值。最后将遗传优化岭回归GM(2,1)预测模型应用于供应链风险预测实例中，验证了模型的可行性与适用性，为供应链风险预测提供了一条有效途径。

[1]周艳菊,邱莞华,王宗润.供应链风险管理研究进展的综述与分析[J].系统工程,2006,24(3).

[2]程书萍,张德华,李真.工程供应链风险源的识别与控制策略研究[J].运筹与管理,2012,21(4).

[3]李民,黎建强.基于模拟方法的供应链风险与成本[J].系统工程理论与实践,2012,32(3).

[4]陈新平.紊乱环境下供应商风险预测模型[J].统计与决策,2011,(6).

[5]史成东,边敦新,苏菊宁.基于粗糙集和灰色的供应链知识共享风险预测[J].计算机工程与应用,2008,4(11).

[6]郑照宁,武玉英,包涵龄.GM模型的病态性问题[J].中国管理科学,2001,9(5).

[7]刘虹,张岐山.基于微粒群算法的GM(2,1,λ,ρ)优化模型[J].系统工程理论与实践,2008,28(10).

[8]刘思峰,党耀国等.灰色系统理论及其应用[M].北京:科学出版社,2010.

[9]郑照宁,刘德顺.灰色系统模型的优化岭回归算法[J].运筹与管理,2004,12(3).

[10]朱尚伟,李景华.岭回归参数的两个预期约束[J].统计与决策,2015,(22).

[11]周峰,孟秀云.基于岭回归径向基神经网络的MIMU误差建模[J].系统仿真学报,2010,(9).

[12]冯宇强,陈五一,陶丛丛,王锋.基于遗传算法的岭回归模型在大坝安全监测中的应用[J].水电能源科学,2010,28(10).