精密导航系统监测数据的模糊综合评价模型设计

邹 岩，张 娜，严小军，耿振野

（1.长春理工大学，长春130022；2.北京航天控制仪器研究所，北京100039）

0 引言

对于精密导航系统来说，性能好坏直接决定了导航精度的表现。因此，针对精密导航系统的监测数据做出低延时的合理评估，为地面测试环境的调试提供及时的评价反馈，对于保障精密导航系统的可靠性和精度是一个十分有价值的研究方向。

在实际测试环境下，在地面测试环境中，依据测试数据的反馈，一部分数据信息由于某些因素存在着可变性、浮动性等特征。精密导航系统的健康水平是根据定量的实时监测数据、定性的测试状态信息以及通过试验积累的专家主观经验来评定。因此，基于测试情况和实际需求的综合考虑，本文参考现有的测试环境设计了一套基于AHP-模糊综合评价方法的精密导航系统监测数据的评价模型。该评价模型从数据的多个属性中给出依据评价指标得到的状态评估信息和被测器件的健康隶属度。

1 精密导航系统监测数据的评价指标体系

模糊综合评价理论是一种建立在以模糊数学为基础之上的评价方式，特点就是通过对评价对象建立模糊数学的数学模型，从而对评价对象进行综合、完整的数学评价，通过分析结果实现最优解选择、数据分析的目的。本文主要研究在已有的监测数据特征参数和健康状态等历史参数的情况下，建立特征参数与导航系统的测试状态之间的模糊评价模型，通过合成算子实现对精密导航系统测试的状态评估，得到被测系统的健康状态信息。

1.1 精密导航系统监测数据的评价指标选取及说明

导航系统的测试对严谨性和实时性都有很高的要求，评价指标要求能够正确并及时地通过监测数据反映被测系统的各部分状态信息。作为评价体系的基础，首先要确定检测数据的评价指标，指标的选取按照功能上分为规范类指标和精度考察类指标两类。

（1）规范类判定指标的选取

监测数据的评估是建立在符合标准和保持高精度的基础上，在标准范围内的判据通过规范类指标体现。偏差度指标作为多个监测指标都要评估的评价指标，反映了被测值和标准值的偏差度。偏差是稳态的，长时间在非额定电压或频率下工作，会严重影响电气设备的使用寿命。该指标拥有 “一票否决”的性质，即任何一项基本偏差性指标无法满足，都会使监测数据的状态评价输出不合格的结果。

（2）精度类考察指标的选取

评价模型除了要对规范类指标进行评估，进一步的评估是由精度类指标体现。精度类的考察指标可以从数据反映的波动幅度、稳定时间等方面进行评价。

其中，电压波动指标是指一段持续的时间里，相关的电压幅值频繁在标准值上下波动且波动范围较大。作为一种动态的监测指标，过大且持续的波动会影响系统的导航精度。

稳定时间是指监测数据的幅值从开始进入稳定值经历的时间，该指标考察了被测数据的动态响应时间。

作为三相电压和三相电流中考察不平衡度属性的指标，三相不平衡度是指三相电力系统中三相不平衡的程度。三相不平衡轻则降低线路的供电效率，重则会因重负荷相超载过多，可能造成某相导线烧断、器件烧坏等严重后果。

1.2 精密导航系统监测数据的评价体系设计

按照模糊层次分析法的设计思路，首先将评价体系分为3层，分别为目标层、类别层、指标层。中间的类别层按照物理相似度分为电源频率、电流、力矩电机电流、电压、温度5类，每类包含多个属性类似的监测指标。按照不同指标的实际物理意义，又在类别层下派生出包含多个评价指标的指标层。图1为精密导航系统监测数据评价指标评价结构体系。

监测数据在指标层会得到评估指标的预处理数据，预处理数据经过隶属度函数的计算得到该项指标的评价结果，逐层向上将评价结果通过对应的模糊算子合成，最终会在目标层汇总成被测系统的监测数据模糊综合评价结果。模糊综合评价的输出流程如图2所示。

图1 模糊综合评价体系Fig.1 Construction of comprehensive fuzzy valuation

图2 模糊综合评价流程Fig.2 Process of comprehensive fuzzy valuation

2 评价指标的隶属度函数设计

模糊综合评价就是对指标的隶属度进行评价，即指标的标准化处理。根据指标特性不同，模糊评价时具有不同的隶属度函数。由1.1节分析叙述可知，按照物理属性进行分类。针对每一类别下的子类别，可以依据不同的指标，选择合适的隶属度函数。

1）偏差指标的隶属度函数如式 （1）所示：

其中，U1和U2为根据实际情况来确定的常数。ΔU 通过式 （2）获得：

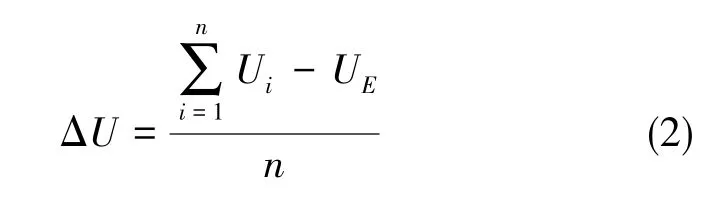
其中，UE为电压的额定标准值（静态偏差）。2）波动幅度指标的隶属度函数如式 （3）所示：

其中，U1为根据实际情况来确定的常数。关于波动幅值的大小可以通过式 （4）获得：

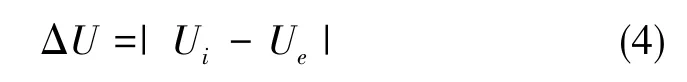
其中，Ue为电压的额定标准值（动态波动）。

3）稳定时间的隶属度函数如式 （5）所示：

其中，TU1和k为根据实际情况来确定的常数。

4）三相不平衡度的隶属度函数如式 （6）所示：

其中，a1和a2为根据实际情况来确定的常数。不平衡度的求取公式如式（7）所示：

其中，Imaxφ为电流最大值，Iav为电流平均值。

3 AHP-模糊综合评价中权重的求取

在多指标模糊综合评价中，不乏与其他综合评判法相结合来确定权重的应用，AHP-模糊综合评价利用模糊一致判断矩阵对各个指标进行重要性的比较，解决了层次分析法在判断矩阵一致性、权重求取方面的问题。同时，利用层次分析法（AHP），亦可以有效解决在多指标模糊评价中，权值分配过小而导致评价结果无法体现单个评价指标的问题。

首先通过参照已知测试结果及历史测试数据，针对每一个类层 （指标层），通过专家打分或专家建议等方式，确定模糊一致判断矩阵。其中，矩阵具有如下性质：

式中，Sij代表第i个指标与第j个指标之间的关系，取值为0.5代表2个指标同等重要，取值越大代表指标i越重要。得到模糊一致判断矩阵后，可以通过权重公式求取每个指标的权重，如式 （9）所示：

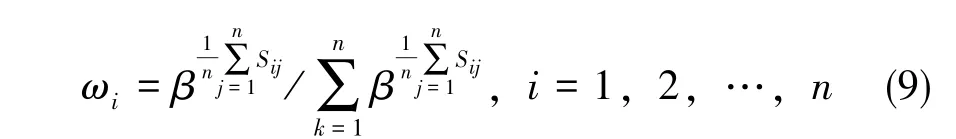
因而， 对于模糊判断矩阵R＝ （rij）m×n有一族权重矢量：

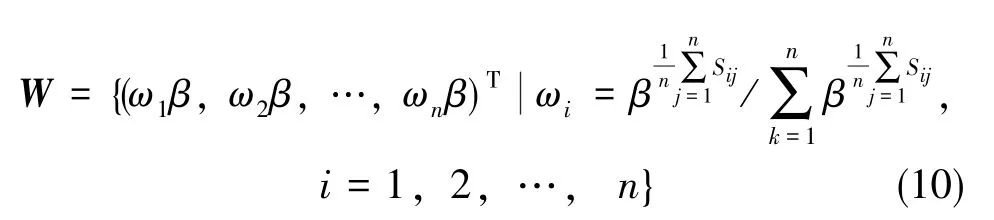
式中，β是大于1的底数，通常参数β＝e5或e3或e。通过增大β的值提高方案优劣的分辨率，但是当β很大时，某些权重值会趋向于零，不利于计算机处理。利用上述权值公式，计算后得到该层下类别层（指标层）每一项权值。

4 评价结果的合成算子设计

在每个类别总结出各自的评价指标后，需要按照规定的权重比，合成多个监测类综合的隶属度评价结果。精密导航系统测试环境中，评价指标具有明显的共同作用特性，现有的以加和、取极值为特性的模糊评价算子已经不能满足评价的需求。在此针对不同的评价指标提出基于多算子的综合评价算子，从而使评价结果更具有可靠性和客观性。

4.1 基于多算子的模糊评价合成

在导航系统的测试环境下，由于评估的指标繁多，评价模型需要对特定的监测数据选定合适的模糊合成算子，保证每个指标都能够在综合的评价结果中得到严谨的反映。针对单一算子下评价结果不严谨的情况，通过设计多算子的模糊合成算子可以有效改善这一问题。

首先，在多个监测量中都出现考察精度的指标，按照一定权重比采用乘加算子得到3个评价结果的合成。乘加算子合成公式如式 （11）所示。

式中，ωi是指标i所属的权重，rij是j类监测量下指标i的隶属度。

其次，对于规范类的指标，即评价指标的取值隶属度为被测系统的某个属性是否合格，评价的合成算子为：

式中，rij为第i个指标的合格隶属度。当某一个指标的合格隶属度较低时，将使整个系统的合格隶属度降低；只有全部指标在合格项隶属度很高的情况下，整体评价的合格隶属度才会很高。

在确定各类评价指标的合成算子后，通过将两种算子相乘的方式，得到基于多算子的模糊评价结果合成公式。算子公式为：

4.2 最小置信度识别准则

得到模糊评价结果后，通常根据最大隶属度识别准则得出该模糊评价的结果。但是，在高精密仪器的测试环境中，针对某些评价结果出现多峰值的情况，这种只选取一组向量中的数值最大项，而并没有考虑到该组向量中的其他项的权重是不合理的。

因此针对评价结果，用最小置信度识别准则来验证其有效性。设评价指标（y1，y2，…，yk）为属性空间Y的有序分割，μx为隶属度，在这要求隶属度向量归一化为置信度，λ的取值范围通常为0.5＜λ ＜1，一般取λ ＝ 0.6～0.7。

5 算例验证与分析

通过结合某型精密导航系统的某次地面测试数据，带入建立好的AHP-模糊综合评价模型，利用监测数据评价和结果分析来验证该评价模型的有效性。

5.1 监测数据指标隶属度求取

参照第2章节隶属度函数的设计方法，依据导航系统监测数据综合评价体系中评估各类监测数据的评价指标，将预处理好的数据带入各指标的隶属度函数，求得各隶属度值。

以电流类为例，自瞄准过程中的监测数据中陀螺马达电源和加速度计马达电源的电流项的多项指标，包括偏差度、波动幅度、三相不平衡度，如图3所示。

图3 陀螺马达电源电流和加速度计马达电源电流Fig.3 Supply currents of gyroscope motor and PIGA motor

由图3可知，陀螺马达和加速度计马达电源的三相电流都存在三相不平衡问题，参考电机相关设计标准，给予2%的不平衡度包络范围。依据隶属度函数选取类型，利用式（7）得到三相不平衡度后，带入式 （6）求得三相不平衡度的隶属度值。其中，参数a2取包络值2%，参数a1用于体现严格符合标准的符合程度，取值0.3%。计算求得的三相不平衡度的隶属度函数图如图4所示。

图4 三相不平衡度隶属度函数Fig.4 Membership function of three-phase unbalance

其他指标依据各自的物理属性，参照上述步骤，通过代入该指标项的预处理数据到评估函数中，可以得到该指标下隶属度值。将隶属度值进行统计，可得到自瞄准中该指标的隶属度分布情况。陀螺马达和加速度计马达电源电流部分的指标评价结果如表1和表2所示。

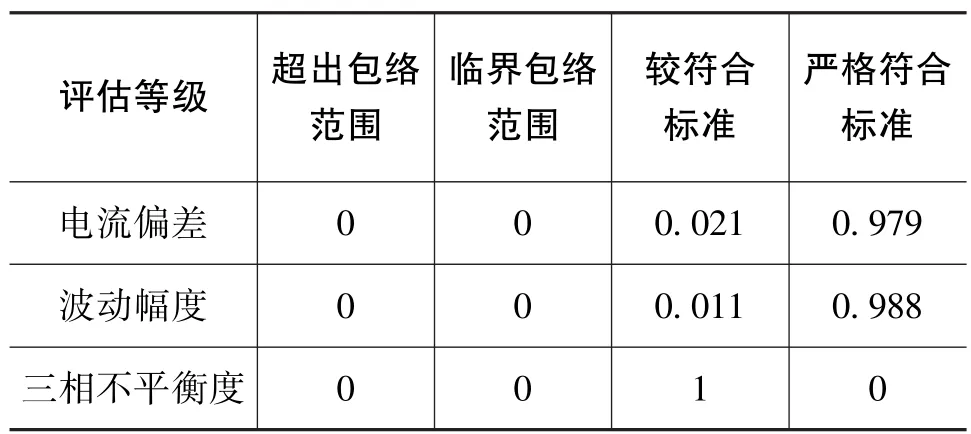
表1 陀螺马达电源电流评估结果Table 1 Evaluate result of supply currents of gyroscope motor

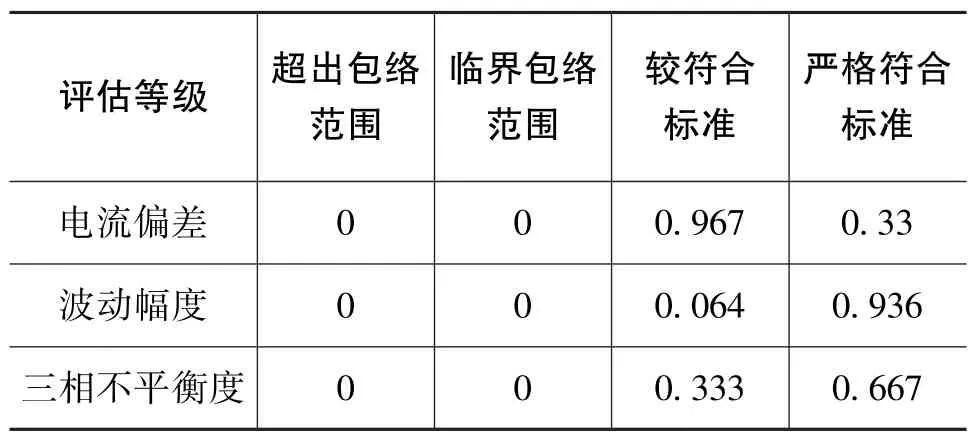
表2 加速度计马达电源电流评估结果Table 2 Evaluate result of supply currents of PIGA motor

5.2 评价指标权重的求取

依据专家建议，确定模糊层次评价的模糊一致判断矩阵，得到各层次的权重值。

以类别层为例，根据电源频率、电流、电压、温度、力矩电机电流的物理属性、算子合成方式以及隶属度判别方法来确定模糊一致判断矩阵，如表3所示。

表3 类别层的模糊一致判断矩阵Table 3 Fuzzy consistent judgment matrix

在权值求取中，分辨率参数β＝ e3， 利用式（10）计算每个指标项的权重，带入对应的指标关系参数Sij，可得到该模糊一致判断矩阵对应的权重系数向量为 ［02230 0.2230 0.2230 0.1754 0.1555］。

同理，可以按照上述计算方式得到指标层的各指标间权重关系，如表4～表6所示。

表4 电源频率指标权重Table 4 Weight of indicators of supply frequency

表5 电源电压权重Table 5 Weight of indicators of supply voltage

表6 温度指标权重Table 6 Weight of indicators of temperature

5.3 评价结果的合成和求取

根据4.1节所述，将不同的指标按照指标类型用规定的模糊算子进行评价结果的合成。规范类评价指标通过0-1乘法算子进行评估结果合成，对于一般评价类指标利用乘加算子进行计算。依据此方法，利用4.1节提出的式 （13）从指标层逐层向上求得如表7的总体综合评价结果。

表7 模糊综合评价结果Table 7 Result of comprehensive fuzzy valuation

5.4 评价结果分析

通过以上的实际算例计算，可以得到该次测试的监测量模糊综合的评价结果。从评估结果中可以看到，在 “严格符合标准”的评价结果下隶属度是78.81%，在4个评价结果中隶属度追高。基于第4章节阐述的最小置信度识别准则，取置信度λ＝0.7，综合结果中，严格符合标准的隶属度追高，且隶属度值0.7881＞0.7，满足最小仔细读识别准则。因此，针对该次测试的结果可以给予严格符合标准的评价结果。

此外，从综合评估结果中还可以看出，接近包络值的隶属度达到0.1136。通过观察类别项的评估结果可以得出，温度项的监测量评估结果中，评估结果的隶属度值在 “接近包络值”和 “较符合标准”也有体现。由此可以具体分析该项中的监测指标，针对这一部分进行改进。

6 结论

本文针对现有精密导航系统的测试环境，提出一种基于AHP-模糊综合评价的监测数据评价模型。同时，提出了多算子的模糊评价结果合成，

用以准确体现不同监测指标的状态特性在综合评价中的作用。最后，利用最小置信度校验准则来验证评价结果的有效性。算例表明，本文提供的方法可以有效得到导航系统在地面测试的综合评价，指标体系结构与评价模型合理，评价结果可为精密导航系统的测试提供意见和参考。

［1］刘毅.基于模糊集理论的多层次船舶安全性评价模型研究［J］. 舰船科学技术， 2016（12）： 127-129.LIU Yi.A multilevel marine safety evaluation model study based on fuzzy set theory［J］.Ship Science and Technology， 2016（12）： 127-129.

［2］岳强，刘福胜，刘仲秋.基于模糊层次分析法的平原水库健康综合评价［J］.水利水运工程学报，2016（2）：62-68.YUE Qiang， LIU Fu-sheng， LIU Zhong-qiu.Comprehensive assessment of plain reservoir health based on fuzzy and hierarchy analyses［J］.Hydro Science and Engineering， 2016 （2）： 62-68.

［3］李连结，姚建刚，龙立波，等.组合赋权法在电能质量模糊综合评价中的应用［J］.电力系统自动化，2007， 31 （4）： 56-60.LI Lian-jie， YAO Jian-gang， LONG Li-bo， et al.Application of combination weighting method in fuzzy synthetic evaluation of power quality［J］.Automation of Electric Power Systems， 2007， 31 （4）： 56-60.

［4］兰继斌，徐扬，霍良安，等.模糊层次分析法权重研究［J］. 系统工程理论与实践， 2006 （9）： 107-112.LAN Ji-bin， XU Yang， HUO Liang-an， et al.Research on the priorities of fuzzy analytical hierarchy process［J］.System Engineering Theory and Practice， 2006 （9）：107-112.

［5］杨家豪，欧阳森，石怡理，等.一种组合隶属度函数及其在电能质量模糊评价中的应用［J］.电工电能新术， 2014， 33 （2）： 63-69.YANG Jia-hao， OUYANG Sen， SHI Yi-li， et al.Combined membership function and its application on fuzzy evaluation of power quality［J］.Advanced Technology of E-lectrical Engineering and Energy， 2014， 33 （2）： 63-69.

［6］郝燕玲，牟宏伟.基于AHP的光学捷联惯导系统综合评价［J］. 舰船电子工程， 2012， 32 （10）： 42-43+104.HAO Yan-ling，MU Hong-wei.Comprehensive evaluation of optical strapdown inertial navigation system based on AHP［J］.Ship Electronic Engineering， 2012， 32 （10）：42-43+104.

［7］石钊铭，王文革.基于灰色多层次综合评价模型的捷联惯性导航系统评估方法［J］.船电技术，2014，34（10）： 29-32.SHI Zhao-ming，WANG Wen-ge.Evaluation method for strap-down inertial navigation system of multi-level based on gray comprehensive evaluation model［J］.Marine Electric ＆ Electronic Engineering， 2014， 34 （10）： 29-32.

［8］荣吉利，张涛，徐天富，等.性能参数型航天器机构的可靠性试验评定方法［J］.宇航学报， 2012，33（3）：387-391.RONG Ji-li， ZHANG Tao， XU Tian-fu， et al.Study on test method of reliability assessment used for performance parameter-measured spacecraft mechanism［J］.Journal of Astronautics， 2012， 33 （3）： 387-391.

［9］杨宝琨，康兴无.基于小样本数据的惯性平台系统贮存可靠度的预测方法［J］.航天控制， 2015，33（5）：90-95.YANG Bao-kun，KANG Xing-wu.Inertial platform system storage reliability prediction method based on small sample data［J］.Aerospace Control， 2015， 33 （5）： 90-95.

［10］苗俊杰，李秉宇，李荣健，等.基于模糊综合评价模型的直流电源监测与评价平台［J］.电源技术，2017，41 （6）： 935-937.MIAO Jun-jie， LI Bing-yu， LI Rong-jian， et al.Monitoring and evaluation platform of DC power supply based on fuzzy comprehensive evaluation model［J］.Chinese Journal of Power Sources， 2017， 41 （6）： 935-937.