基于制造特性的马达轴孔装配有限元分析
(北京理工大学微小型制造研究所,北京100081)
0 引言
研究表明精密马达系统中的马达轴装配体是影响系统运行特性的主要机械结构,而马达轴孔装配精度直接影响马达轴质心位置偏移,进而影响整个系统的实际使用性能。在零部件的加工精度已达到精密甚至超精密制造水平的情况下,装配后的结构精度却难以满足设计要求,主要原因在于装配过程中忽视了零件制造特性[1]引入的装配误差,直接影响了马达轴孔装配精度。
北京理工大学微小型制造研究所[2-4]致力于精密微小型零件的制造特性对精密系统装配性能影响研究,并取得了较为系统的研究成果。张之敬、金鑫等以精密微小型结构件为研究对象,深入分析零件制造误差对机构运行特性的影响,保证了机构运行准确性和可靠性;此外,基于Pro/E的逆向工程技术重构了实际误差表面,仿真分析了误差面接触应力分布及装配体精度变化情况。Cheon等[5]采用混合有限元方法分析了制造误差对行星齿轮系统的静态性能和轴承支承刚度的影响,并建立了基于承载力和临界应力的公差控制准则。Haefner等[6]采用高精度三维测量设备测量微齿轮表面形状误差,并建立CAD模型,用以研究建立合适的疲劳寿命预测模型。Wang等[7-8]以实际涡轮增压器为研究对象建立了带有浮环轴承的动力学有限元模型,并根据内外环油膜的极限间隙确定了4种轴承误差状态,结果表明外环间隙最小和内环间隙最大时可以获取最好的动态响应特性。Jia等[9]建立了带有制造误差的高速转子有限元模型,分析了平行度误差和对称度误差对转子力学性能及动力学特性的影响机理,结果表明转子的应力和应变与制造误差呈线性变化关系,而高速转子的固有频率基本保持不变。
上述研究成果表明,零部件制造特性对机械系统性能有不可忽视的影响,尤其是对于精密机械系统,忽略制造误差而得到的仿真结果往往与实际相差甚远。本文针对精密马达系统中的马达轴孔装配体建立考虑制造特性的仿真模型,分析制造误差和装配力等引起的关键接触面应力分布状态和马达质心位置变动,并依据仿真结果确定优化区域和优化方法,为装配工艺优化提供理论指导和技术支撑。
1 误差测量与三维建模
精密马达系统中的马达轴孔装配结构体如图1所示。装配过程中的关键操作工艺在于将马达轴放置于框架两个半圆孔上,上端采用压盖压紧并通过螺钉紧固。框架半圆孔的制造误差直接影响马达轴孔装配精度,最终影响马达质心位置。

图1 马达轴孔装配体模型Fig.1 Assembly model of motor shaft
基于Pro/E逆向工程建立带有制造误差的三维实体模型,首先采用三坐标测量机测量框架孔表面形貌特征,如图2所示。三坐标测量机精度为(2.5±L/1000)μm,在径向测量19个点,轴向测量6圈;在完成表面形貌的数据点云测量工作之后,利用Matlab对测量数据进行滤波处理,而后构建NURBS曲面,最终得到带有制造误差的实际半圆孔表面;将该误差面输入Pro/E,并替换掉理想面,得到带有实际制造误差的框架三维实体模型。

图2 三坐标测量框架半圆孔Fig.2 Measuring frame hole with three coordinate measuring machine
带有制造误差的孔表面不再具有理想几何形状,若马达轴仍按照理想轴线装配,则马达轴和框架必然产生干涉或者间隙,不符合实际装配操作并难以进行接触仿真计算。本文基于最小势能寻优方法[10]寻找误差面装配接触点,首先将同一装配坐标系下的框架半圆孔和马达轴圆柱面离散为相同规格的数据点并分别记为和。
以静水压力势能表征各个接触面的势能,则接触面上每一点势能表示为:

其中,W为每个点的势能,ρ为静水密度,h为装配坐标系下每个点深度方向坐标值(本文中为z向)。
最小势能寻优是指改变两个装配接触面的位姿状态,使得总势能最小,这是符合实际装配情况的最稳定状态。以框架半圆孔表面各点为势能零点,则马达轴圆柱面各点势能以此相对零点进行计算,寻优目标为两者势能总和取得最小值,优化条件为马达轴和框架不发生干涉,即马达轴表面各点势能均≤0, 如式 (2)、 式 (3)所示:
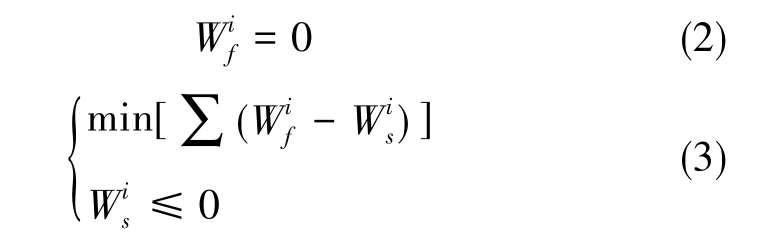
其中,为框架半圆孔表面各点势能,为马达轴表面各点势能,i=1,2,3…。
根据整体势能最小时的马达轴位姿反求出原始装配接触点坐标,将该坐标分别输入框架和马达轴零件模型,并依据相应坐标重合完成两者装配。马达轴孔装配体误差测量与三维建模流程如图3所示。

图3 基于制造误差的三维实体建模流程Fig.3 Three-dimensional solid modeling process based on manufacturing errors
2 有限元仿真模型的建立
基于上述带有制造误差的三维实体装配模型建立装配体仿真模型,由于实际框架模型的微小特征不利于网格划分,并且对仿真结果影响较小,因此为了建立有效的有限元模型,首先对实际框架结构进行简化,通过去除框架两端微小沟槽特征达到有效建模和控制模型规模的目的。如表1和表2所示,在HyperMesh中完成材料参数设置和网格划分。网格划分应充分考虑精确性、单元形状良好性、网格有效过渡性和网格自适应性,最后通过.inp文件将网格模型导入Abaqus并设置边界条件、载荷、相互接触作用和求解器等仿真参数。

表1 材料属性Table 1 Material properties

表2 网格参数Table 2 Mesh parameters
为了有效模拟框架轴两端的磁悬浮支承,选用Abaqus提供的特殊连接单元Bushing,该单元能够实现6个分量的弹塑性行为模拟,且能够分别定义每个分量的弹性、阻尼和摩擦等参数。根据实际磁悬浮支承力换算得到6个分量的相应数值,并赋予框架轴两端的Bushing连接单元,以有效模拟实际工作环境中框架的边界条件约束。采用软件提供的Bolt Load预紧力单元模拟实际螺钉预紧力,预紧力单元通过一个预紧节点与定义的预紧力截面相绑定,对节点施加集中力并传递给预紧截面来模拟实际螺钉预紧过程。该节点只有一个自由度,用于表示预紧截面两侧在截面法线方向的相对位移,该节点的坐标位置不影响仿真效果,且在软件交互界面下不可见。
采用Bolt Load预紧力单元模拟螺钉预紧过程时需要输入预紧力大小,而实际工程中多规定扭矩值,因此两者之间通过式 (4)进行转换:

其中,k为拧紧力矩系数,文中取0.3;T为拧紧力矩;F为预紧力;D为螺钉公称直径。经过换算得到马达轴孔装配体中的标准螺钉预紧力为500N,将此数值输入预紧力单元即可。
由于框架和马达轴装配接触面为多个点和圆柱面的接触,加强了仿真模型的非线性,在仿真计算过程中设置接触稳定性控制,以避免由于非均匀接触导致的计算不收敛情况;为了保证仿真计算的准确性和提高仿真精度,选用静力学隐式算法直接求解。为了简化有限元模型前处理工作量,上述操作均在Abaqus CAE界面下完成,最终建立带有制造误差的马达轴孔装配体有限元模型,如图4所示。

图4 基于制造误差的马达轴孔装配体有限元模型Fig.4 FE model of motor shaft assembly based on manufacturing errors
3 装配力学特性有限元分析
3.1 制造误差对马达轴孔装配精度的影响
基于第四强度理论采用Mises等效应力分析马达轴孔装配后的误差接触面非均匀应力大小,研究制造误差对框架和马达轴装配接触面应力分布的影响,并分析制造误差引起的马达质心位置变动。对比误差仿真模型和理想仿真模型中框架半圆孔接触面应力分布如图5所示,两类模型均施加标准螺钉预紧力500N。
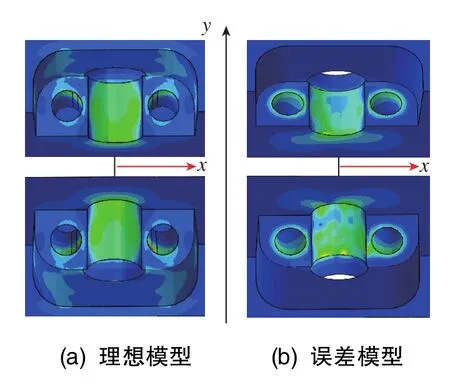
图5 理想模型和误差模型接触面应力分布Fig.5 Stress distribution on the contact surface of ideal model and error model
从图5可以看出,制造误差导致接触面应力呈现明显不均匀分布状态,且接触面上存在多处应力集中点,这些应力集中点为误差面上的高点,直接参与框架和马达轴的接触。长时间的放置或运行使得接触点受到磨损,同时新接触点的出现改变了接触作用位置并影响马达轴孔装配精度,进而使得马达质心位置处于动态变化中,因此接触面上的不均匀应力分布和应力集中会影响马达质心的稳定性。
理想模型和误差模型中马达轴孔装配体变形如图6所示,制造误差直接改变了马达轴理想装配位姿和装配体结构变形,影响了马达轴孔装配精度。从表3可以看出,制造误差对马达轴质心偏移有显著增大趋势,因此制造误差对精密马达系统有重要影响且不容忽视,研究基于制造误差的建模和仿真具有实际指导意义。
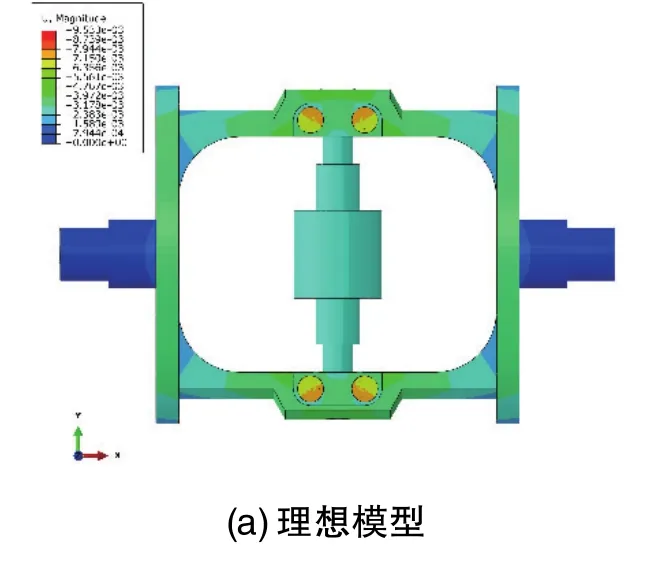

图6 理想模型和误差模型变形图Fig.6 Total deformation of ideal model and error model

表3 马达轴质心位移Table 3 Centroid deviation of motor shaft
3.2 螺钉预紧力水平对马达质心位置的影响
马达轴孔装配结构体主要通过螺钉紧固连接,现有装配工艺主要依据装配工艺师的经验手动完成螺钉预紧。经过测量多位马达产品装配师对螺钉施加的拧紧力矩,发现仅凭手感拧紧后的螺钉力分散度较大,多次拧紧后的螺钉力一致性较差,对最终的马达轴孔装配精度影响差异性明显。经过实际测量装配师拧紧后的螺钉扭矩,其数据分布在335N~590N之间,因此对所有螺钉分别取预紧力300N、400N、500N、600N和700N这5种情况,分析不同预紧力对马达轴质心位置的影响规律。
图7为不同预紧力作用下的马达轴质心在各个方向分量和总位移的变化趋势。可以看出,马达轴质心位移 (绝对值)变化规律与预紧力具有一致性,且每增加100N,质心总位移大约增加8%,因此预紧力对质心位移有显著影响。除了制造误差的影响,预紧力导致的马达轴质心偏移主要来自于框架本身结构特性。由于框架结构刚度较差,框架变形的同时带动了马达轴变形和质心偏移,影响了马达轴孔装配精度和马达系统的质心位置。因此,在装配空间允许范围内修正框架几何结构,增强其结构刚度,可在一定程度上减小马达轴质心偏移,提高马达轴孔装配精度,增强精密马达系统的质心稳定性。

图7 马达轴质心位移变化趋势图Fig.7 Effect of preloading levels on centroid deviation of motor shaft
3.3 螺钉拧紧顺序对马达质心位置的影响
实际马达轴孔装配过程中存在螺钉拧紧顺序不一致的情况,两个螺钉作用于同一个压块,其螺钉间的弹性相互作用会改变已拧紧螺钉的预紧力大小,导致装配体中实际螺钉预紧力不一致。通过分析不同拧紧顺序对马达质心位置的影响,选取合适的拧紧顺序减小马达轴质心偏移,提高装配精度。对马达轴孔装配过程取6种不同的螺钉拧紧顺序,如图8所示。
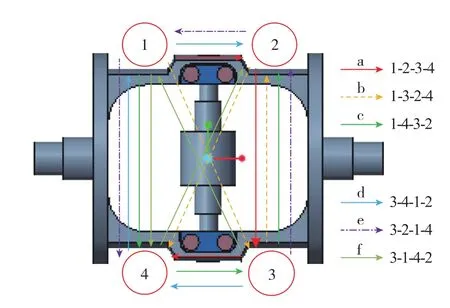
图8 螺钉拧紧顺序Fig.8 Screw tightening sequence
施加螺钉预紧力时,采用多步加载的方式模拟螺钉拧紧的先后顺序。以拧紧顺序a为例,从计算结果中提取4个螺钉预紧力随时间变化趋势,如图9所示。从图9(a)可以看出,预紧力变化分为以下几个阶段:第1阶段施加较小的螺钉力,建立接触关系;第2阶段为接触稳定性控制;第3阶段为全部螺钉加载预紧力300N;第4阶段为分步依次加载预紧力500N。该加载方式比较贴近实际拧紧过程,能较大程度反应实际螺钉拧紧后的残余预紧力。
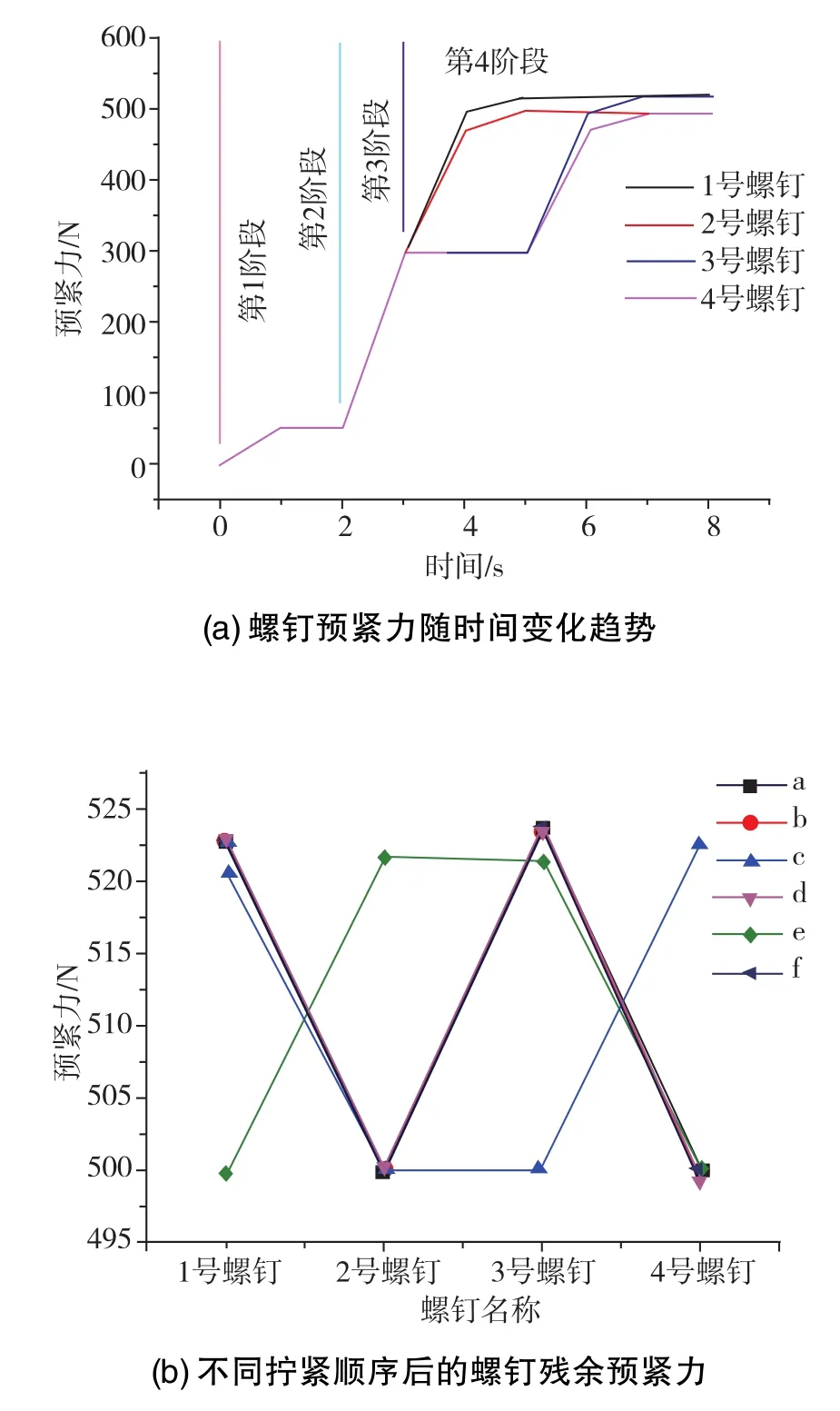
图9 多步加载螺钉预紧力变化趋势图Fig.9 Change of screw preload with multi-step
进一步比较分析马达轴孔最终装配后的残余预紧力与标准预紧力500N的差异性,发现先拧紧的螺钉最终预紧力增加了大约5%,这仅影响同一压块两侧的螺钉,对其余螺钉无直接影响。对马达轴质心偏移进行分析,如图10所示。拧紧顺序d得到的马达轴质心位移最小,且各个分量具有相同的变化趋势;由于同一批零件的加工误差分布具有一致性,因此在实际拧紧工艺中,采用d拧紧顺序可减小马达轴质心偏移,提高马达轴孔装配精度。

图10 马达轴质心偏移Fig.10 Effect of tightening sequence on centroid deviation of motor shaft
3.4 螺钉预紧力大小对马达质心位置的影响
对考虑了接触面表面制造特性的精密马达轴孔结构体,分析不同预紧力大小及分布状态对马达轴孔装配精度的影响,进一步控制马达质心位置的变动。根据标准预紧力500N得到的马达轴质心偏移,调整预紧力大小如表4所示。调整的基本原则为增大质心偏移方向的螺钉预紧力,并减小反方向预紧力。

表4 螺钉预紧力调整表Table 4 Adjustment of screw preload
分析上述预紧力作用下的马达轴质心偏移,如图11所示。从图11可以看出,预紧力调整后的马达轴质心偏移有明显变化,X和Y方向质心偏移明显减小,Z方向质心偏移主要取决于整体预紧力大小,与几何结构刚度有关,且质心偏移对2号、4号螺钉预紧力敏感度较高。因此在实际工程中,可通过优化预紧力大小及分布状态提高装配精度和控制质心位置,具体优化方法需根据实际产品中关键零部件制造特性而确定。
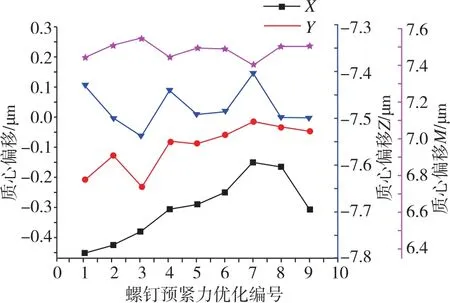
图11 预紧力优化后的马达轴质心偏移Fig.11 Centroid deviation of motor shaft after optimizing the screw preload
4 结论
本文通过对马达轴孔结构体中关键接触面进行了误差测量和建模,采用基于最小势能寻优方法确定装配面接触点并建立了装配体仿真有限元模型。通过分析理想模型和带有制造特性的误差模型的接触面应力分布及马达轴质心偏移,得出了制造特性对精密马达轴孔装配仿真有重要影响且不容忽视,是仿真预测装配精度和质心位置必须考虑的因素。针对螺钉装配力开展了装配特性分析,研究了螺钉力大小、拧紧顺序及分布状态对马达轴质心偏移的影响规律,并指出修改几何结构以提高结构刚度、控制螺钉拧紧顺序和螺钉力分布状态来提高装配精度和控制马达质心位置的基本方法,为精密马达轴孔装配工艺及其优化方法的提出奠定了基础。
[1]毛起广.表面粗糙度的评定和测量[M].北京:机械工业出版社,1991.MAO Qi-guang.Evaluate and measure of surface roughness[M].Beijing: China Machine Press, 1991.
[2]金鑫,张之敬,刘克非.面向微小型齿轮-轴过盈装配的仿真建模与验证[J]. 机械, 2004, 31 (9): 1-3+18.JIN Xin, ZHANG Zhi-jing, LIU Ke-fei.Simulation model building and validation of microminiatute gear&shaft shrink fitting[J].Machinery, 2004, 31 (9): 1-3+18.
[3]张之敬,张国智,金鑫.基于制造特性的微小型擒纵机构有限元仿真[J].北京理工大学学报,2007,27(10): 859-863.ZHANG Zhi-jing, ZHANG Guo-zhi, JIN Xin.Finite element simulation of microminiature escapement mechanism based on its manufacturing characteristics[J].Transactions of Beijing Institute of Technology, 2007, 27 (10):859-863.
[4]吕亮霞.基于制造特性的螺旋慢波结构装配性能仿真与优化[D].北京理工大学,2016.LYU Liang-xia.Simulation and optimization of the assembly performance for the helical slow wave structure based on manufacturing characteristics[D].Beijing Institute of Te-chnology,2016.
[5]Cheon G J, Parker R G.Influence of manufacturing errors on the dynamic characteristics of planetary gear systems[J].KSME Internationa Journal, 2004, 18 (4): 606-621.
[6]Haefner B,Quiring M, Gullasch J, et al.Finite element simulation for quality dependent lifetime analysis of micro gears [J].Procedia Cirp, 2015, 31: 41-46.
[7]Wang L K, Bin G F, Li X J,et al.Effects of floating ring bearing manufacturing tolerance clearances on the dynamic characteristics for turbocharger[J].Chinese Journal of Mechanical Engineering, 2015, 28 (3): 530-540.
[8]Wang L K, Bin G F, Li X J, et al.Effects of unbalance location on dynamic characteristics of high-speed gasoline engine turbocharger with floating ring bearings[J].Chinese Journal ofMechanicalEngineering, 2016, 29 (2 ):271-280.
[9]Jia M H, Wang C L, Ren B.Manufacturingerror effects on mechanical properties and dynamic characteristics of rotor parts under high acceleration[J].Chinese Journal of Mechanical Engineering, 2017, 30 (4): 920-932.
[10]房燕.基于非线性接触的精密光学结构装配耦合误差形成与传递机理[D].北京理工大学,2017.FANG Yan.Assembly coupling error formation and transfer mechanism in precise optical structure based on nonlinear contact[D].Beijing Institute of Technology, 2017.

