近邻数据分类器在多目标跟踪中的应用研究

韩春雷，蔚 婧

(1.中国电子科技集团公司第二十研究所，陕西 西安 710068；2.西北工业大学 航海学院，陕西 西安 710072)

在分布式的多传感器多目标探测系统中，一个关键问题是如何判断探测到的数据来自哪个目标，它实际上是要确定空间传感器探测到的信号与不同目标之间的对应关系[1-5]。

多目标探测在智能监控、视频检索、导航、定位等多个领域都有重要的应用，只有将探测到的目标进行正确分类，后续的目标特性提取、参数估计等后续处理工作才有价值。然而，在多目标、干扰、交叉航迹等场合下，由于运动场景及目标数目的不确定性，多目标分类问题往往变得十分困难[6-8]。因此，针对多目标的快速、高效分类方法值得科研人员进行更进一步的研究。

现有的目标分类方法，主要划分为两类：基于概率密度的方法和基于判别函数的方法。基于概率密度的方法主要借助于贝叶斯理论体系，采用潜在的类条件概率密度函数的知识进行分类；基于判别函数的方法使用训练数据估计分类的边界来完成分类[9-12]。目前被证实有效的分类算法有近邻分类器、朴素贝叶斯分类器、支持向量机、决策树算法等。其中近邻数据分类器计算量小，便于实现，在实际工程中广泛采用。

1 近邻分类算法

近邻法是距离度量学习方法中的一种，其在对样本进行分类时，是根据查询样本最近的k个近邻的标签来将其分类[13]。因此近邻法又被称为k近邻法。当k=1时，称最近邻法。

近邻法由Cover和Hart提出，具体思路是：对于一个待识别目标，系统在训练集中找到最近的k个近邻，看这k个近邻中的多数属于哪一类，就把待识别的目标归为哪一类。

其数学表达为：设有n个样本{(x1,y1),(x2,y2),…,(xn,yn)}和一个待分类样本x0。k近邻法对样本进行分类时，首先要计算x0与每个样本的距离，然后找出距x0最近的k个样本，即k个近邻。设共有C个类别{w1,w2,L,wc}，w1，w2，L，wc是k个近邻中属于类别{w1,w2,L,wc}的个数，则判别函数可写为

gi(x)=mi,i=1,2,…,c

(1)

决策函数为

(2)

则x0=wj，即x0归入wj类。

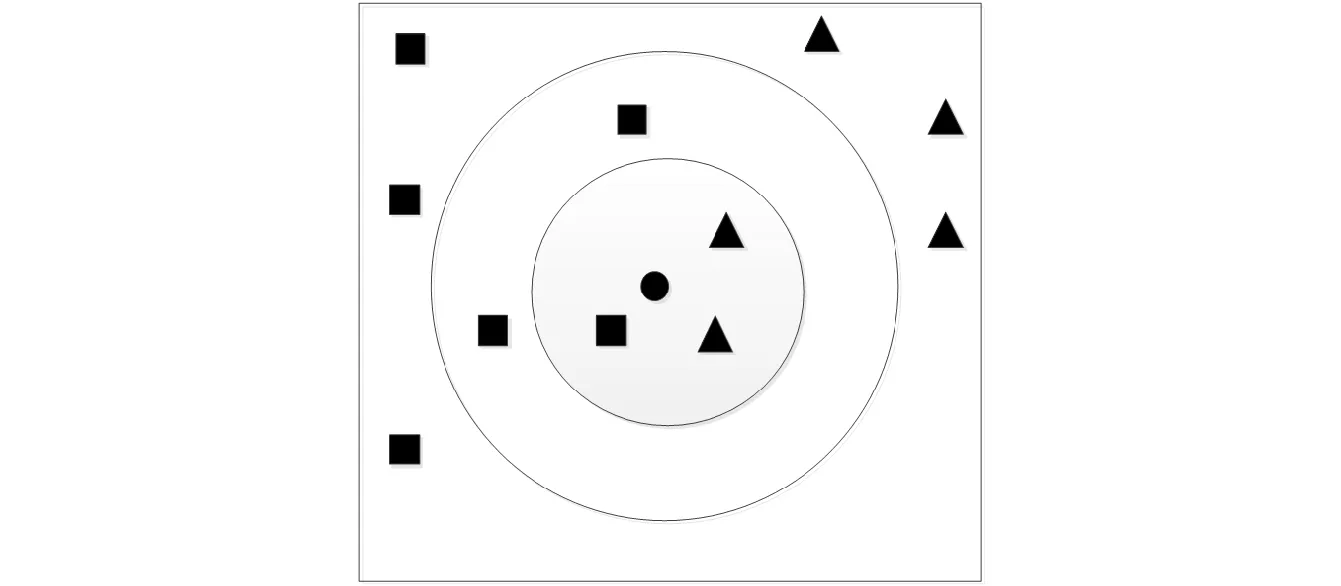
图1 k近邻法示意图

如图1所示，圆圈代表待分类样本，方块和三角形分别为两类已经分类的样本。根据近邻方法的思想 ，当k=3时，有2个样本属于三角形，1个样本归于方块，则圆圈归类到三角型类。当k=5时，有2个样本属于三角形，3个样本属于方块，则圆圈归到方块类。

可见，近邻法当选取的k值不同时，会有不同的分类结果，由此造成分类算法的不稳定性。

2 基于质心分布的近邻分类算法

定义质心为待分类样本与最近的m个已分类样本的距离均值

(3)

在原始的k近邻法中，针对一个待分类样本可能存在多个k值都能将其正确分类，这时普遍采用的方法是随机取一个最小的k值将其分类。但这样随机的选择会使分类存在较大波动，不利于正确分类。

式(3)所定义的质心，实质上是k个近邻样本距待测样本距离的均值。此时，如果待测样本越靠近近邻样本的中心，则对待分类样本的分类预测会越准确。

将质心的概念引入之后，改进的近邻法的实现方法为：用待分类样本与质心的距离来代替待分类样本与训练样本之间的距离。这一做法实质是将k个近邻样本之间的距离变小，而拉大了类间的距离，这一改近更有利于正确分类。

实现步骤：

(1) 设定参数k；

(2) 计算待分类样本x0与所有已分类样本的距离di；

(3) 选取k个最短距离d1，d2，L，dk，确定k个最短距离样本所在的类别{w1,w2,L,wc}；

(4) 计算在每个类别wi中，样本的质心dwi；

3 分布式多目标跟踪系统

由于近年来传感器网络的广泛应用，分布式目标跟踪系统在目标跟踪领域成为主要的研究对象。分布式目标跟踪系统由多个分布在一定距离范围的传感器对同一区域进行观测，对观测到的目标进行联合跟踪[14-16]。

图2 分布式多目标跟踪系统示意图

如图2所示，为典型的分布式多目标跟踪系统示意图，其中有3个观测站对两个目标进行观测。以直角坐标系，匀速运动目标1为例来分析分布式多目标跟踪系统的数学模型。系统的动态模型可以描述为

X(k)=F(k,k-1)X(k-1)+W(k)

(4)

(5)

其为系统的转移矩阵，Ts代表采样周期。

假设观测站位于坐标(0,0)处，观测量为目标斜距和目标方位角，系统的观测模型可以描述为

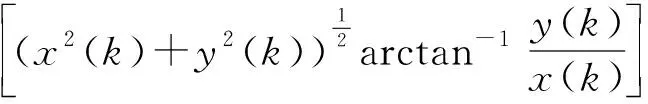
(6)

其中N(k)为高斯白噪声序列，并满足E[N(k)]=0，E[v(k),v(j)]=σ2δkj。

k时刻，量测集合可以表示为Z(k)=[z1(k),L,zm(k)]，其中m表示观测站的数目。而针对每个观测站，量测集合中也是包含了多个目标的量测数据。

目标跟踪的目的是要根据当前时刻对目标的观测，估计出目标的运动状态，进而对下一时刻目标的位置、速度等信息进行预测。因此，首先要对各观测站的观测数据按不同目标进行分类，分类的准确性直接影响后续目标跟踪及航迹预测，所以具有相当重要的意义。

4 应用与分析

基于质心分布的近邻分类算法应用于分布式多目标跟踪系统，验证其分类有效性。

4.1 数据分类实验

为证明本文提出的基于质心分布的近邻分类算法的有效性， 对如图3所示的3类样本进行分类实验，图中的3类样本分别用圆圈、星号、方块表示。

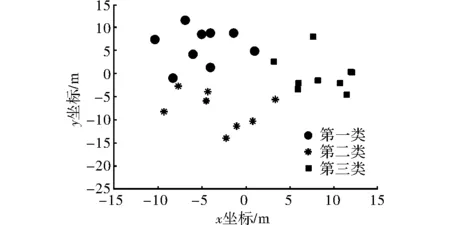
图3 3类样本示意图

用近邻分类算法对图3的样本分类结果如图4所示，分到同一类的样本用直线相连接，从图4所示，共有27个样本，其中23个样本分类正确，4个样本分类错误，分类正确率为85%。

图4 近邻分类算法分类结果

用本文提出的基于质心分布的近邻分类算法分类结果如图5所示，同样将分到同一类的样本用直线连接，27个样本全部分类正确，分类正确率达100%。由此可见，本文所提出的改进算法具有良好的分类特性。

图5 基于质心分布的近邻分类算法

4.2 多目标跟踪实验

实验参数：观测站数目2，目标数据3，采样间隔1 s，角度观测方差1°，距离观测方差10 m，3个目标做匀速直线运动，速度分别为20 m/s，15 m/s，20 m/s。

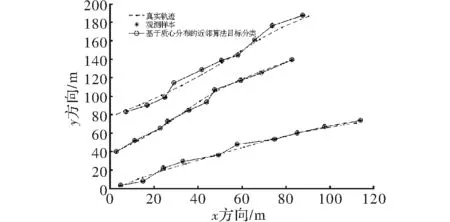
图6 多目标分类示意图

如图6所示，虚线表示目标的实际运动轨迹，星号表示观测到的目标样本，由于在观测环境中存在3个运动目标，所以将运用基于质心分布的目标分类方法分类后的目标用带圈实线连接起来，如图所示，本文方法能够较好地区分3类目标，即使在目标距离比较近的情况下也能很好的区分，再一次验证了算法的有效性。

5 结束语

本文针对近邻数据分类器进行了深入研究，对其分类不稳定性进行了分析，并提出了改进的基于质心分布的近邻数据分类方法。该方法用待分类样本与质心的距离来代替待分类样本与训练样本之间的距离，从根本上减小了样本间距离，增大了类间距离，提高了分类正确率。然后，将提出的改进分类算法应用于分布式多目标跟踪中，将同一个观测站对不同目标的观测数据进行分类，提高了后续跟踪处理结果的可靠性。计算机仿真分析验证了所提方法的有效性，同时表明该分类方法在多目标跟踪系统中具有一定的应用价值。

[1] Hlinka O,Hlawatsch F,Djuric P M.Distributed particle filtering in agent networks:A survey, classification, and comparison[J].IEEE Signal Processing Magazine,2013,30(1):61-81.

[2] Olfati-Saber R,Jalalkamali P.Coupled distributed estimation and control for mobile sensor networks[J]. IEEE Transactions on Automatic Control,2012,57(10):2609-2614.

[3] Wenling L,Yingmin J.Consensus-based distributed multiple model UKF for jump Markov nonlinear systems[J].IEEE Transactions on Automatic Control,2012,7(1):227-233.

[4] Dimakis A G,Kar S,Moura J M F,et al.Gossip algorithms for distributed signal processing[J].Proceedings of the IEEE,2010,98(11):1847-1864.

[5] 方德亮,冉晓旻,李鸥.一种能量有效的分布式传感器管理算法[J].西安电子科技大学学报,2017,44(2):171-177.

[6] 司锡才,陈玉坤,李志刚.数据关联算法的研究[J].哈尔滨工程大学学报,2007,28(7):813-817.

[7] 陈晓,李亚安,蔚婧.一种海杂波背景下的目标跟踪数据关联方法[J].鱼雷技术,2016,24(5):334-339.

[8] Boumediene M, Ouamri A, Dahnoun N. Lane boundary detection and tracking using NNF and HMM approaches[C].Istanbul:2007 IEEE Intelligent Vehicles Symposium,2007.

[9] 曹作宝,包晓敏,汪亚明,等.基于Kalman预测和K-近邻的多目标跟踪[J].浙江理工大学学报,2011,28(3):384-388.

[10] Liu Qingfeng,Liu Chengjun.A novel locally linear KNN method with applications to visual recognition[J].IEEE Transactions on Neural Networks and Learning Systems, 2017,28(9):2010-2021.

[11] Mao Rui,Xiang Peng,Zhang Dian.Precise transceiver-free localization in complex indoor environment[J].China Communications,2016,13(5): 28-37.

[12] 张庆久.近邻法与多视角学习的理论与算法研究[D].上海:华东师范大学,2011.

[13] Liu Xianglong,Li Zhujin,Deng Cheng,et al.Distributed adaptive binary quantization for fast nearest neighbor search[J].IEEE Transactions on Image Processing,2017,26(11):5324-5336.

[14] Cai He,Hu Guoqiang.Distributed tracking control of an interconnected leader-follower multiagent system[J].IEEE Transactions on Automatic Control,2017,62(7): 3494-3501.

[15] Wen Guanghui,Yu Wenwu,Xia Yuanqing,et al.Distributed tracking of nonlinear multiagent systems under directed switching topology: an observer-based protocol[J].IEEE Transactions on Systems, Man and Cybernetics: Systems, 2017,47(5):869-881.

[16] 付强,王刚,郭相科,等.临空高速目标协同探测跟踪需求分析[J].系统工程与电子技术, 2015,37(4):757-762.