基于矢量信号发生器的Galileo E1信号模拟与验证
杜 蒙,宋茂忠,熊 骏
(南京航空航天大学 电子信息工程学院,江苏 南京 211106)
Galileo信号模拟源可以为Galileo接收机的设计与测试提供良好的仿真环境,具有很高的研究价值[1-4]。接收机与卫星之间的相对运动产生的多普勒频移是Galileo信号模拟源设计的关键所在,文献[5]从整体架构上论述了Galileo软件模拟源的各个实现步骤,但没有提及接收时刻的信号模拟算法,也没有给出动态多普勒的实现方法。
本文推导了Galileo E1中频信号的数学模型,实现了一种Galileo E1信号模拟算法,该算法以接收端接收时刻作为时间基准,反推信号传输时刻,利用时间压扩特性[6],实现接收端Galileo卫星导航信号的模拟。该算法逻辑简单,精度与运算时长可控。最终结合矢量信号发生器,用硬件接收机对生成的信号进行测试验证,证明了该算法的有效性和正确性。
1 Galileo中频信号数学模型
Galileo接收机接收时刻简化的Galileo信号模型[7]可表示为

(1)
其中,Pr为接收信号的功率;Di为第i颗卫星的导航电文;Ci为第i颗卫星的伪随机码;SC为子载波;τco,τca和τsc分别为第i颗Galileo卫星信号在时刻t对应的传播过程中的伪码延时,载波延时和子载波延时[8];fE1为E1频段中心频率;sn(t)为噪声信号;smp(t)为多径误差信号。
根据文献[8],载波的多普勒频率变化可以通过时间压扩关系表示
fd·t+fE1·τca=0
(2)
其中,fd为载波多普勒频率。
Galileo信号被天线接收后,经过混频、滤波,变为中频信号,设本地振荡器产生的波形为sos(t)=2cos(2πfost),将式(2)带入,中频信号可表示为

(3)
其中,fIF=fE1-fos,为中频。
根据GNSS定位原理,在三维空间中,为了消除接收机与卫星间钟差的影响,需要4颗及以上卫星才能进行空间定位,为了模拟出可用于定位的Galileo卫星导航信号,需要建立多颗卫星到达信号模型。与单颗卫星的信号模型类似,N颗卫星的信号模型可以表示为

(4)
2 模拟实现
2.1 传输时间计算与误差模拟
卫星信号传输时间取决于实际传输距离,精准计算出信号传输距离是反推卫星发射时刻的必要条件。Galileo系统采用基于Galileo地球参考框架(GTRF)的ITRF-96大地坐标系对卫星位置进行计算、播发,该坐标系与GPS采用的WGS-84坐标系同属地心地固坐标系[10],在信号传输过程中,卫星坐标会因地球的自转而改变,影响对应时刻信号传输距离的计算。为加快计算速度,减少迭代次数,需初始化一个合理的传输时间,然后对卫星位置与传输时间进行收敛迭代,最终当迭代结果满足精度需求时,即得到了指定时刻的真实信号传输时间,算法流程如图1所示。
图1所示迭代算法计算的是理想状态下信号在真空中的传播时间,但在实际的自然环境中,包含着各种可能导致传播速率变化的因素,其中影响较大的有电离层延迟与对流层延迟。
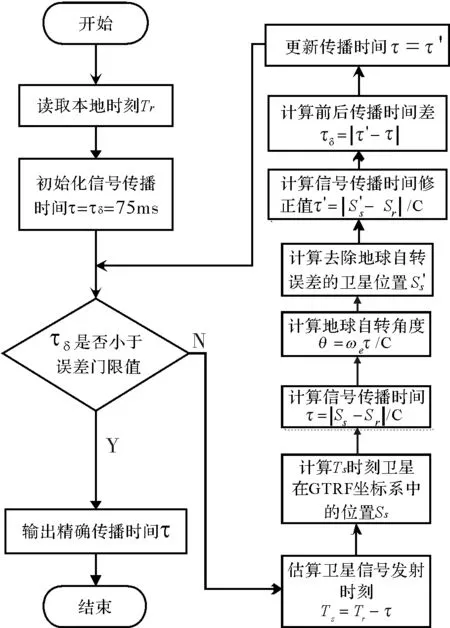
图1 迭代算法流程
电离层由于构成的特殊性,信号在其中的传输速率会产生一定变化,导致一些基于信号传播时间进行距离计算的应用系统产生计算误差,为了产生真实可用的Galileo卫星导航信号,必须在信号中添加电离层误差。本文采用Klobuchar模型[11]计算电离层误差,相关计算参数来源于Galileo导航电文的Az字段。
对流层的存在同样会对卫星信号的传输产生影响,卫星信号的传播延迟在对流层中随高度角余弦的增大而增大,由对流层延迟导致的误差最大能达到约80 m。本文采用Hopfeild模型[11]修正对流层传输延迟,可以将对流层的影响减少至10%以内。
2.2 传输时间拟合与多普勒跟踪
由于卫星与接收机存在相对运动,使接收到的信号产生了频率变化,这种现象称为多普勒效应[12]。根据式(2)可知,载波多普勒与载波延时存在着转换关系,只要确定了某个时刻的载波传输延时就可以确定对应的多普勒频率。关于码相位与子载波相位的计算,可通过信号传输时间反推发射时刻,确定周期内时间偏移,得出包含多普勒频率的相位控制字。为了实现信号多普勒的动态跟踪,本文通过计算等时间间隔抽样点的传输时间,采用三阶多项式拟合任意时刻传输时间,构建信号生成模型。
设i时刻的传输时间为τi,j时刻的传输时间为τj,两个时刻之间的时间间隔为Δt,三阶多项式的系数分别为k1、k2、k3,它们之间的关系可以表示为
τi=τj+k1Δt+k2Δt2+k3Δt3
(5)
i时刻与j时刻的信号传输时间通过图1所示的迭代算法计算得到,为计算三阶多项式系数k1、k2、k3,至少需要3个类似的方程,为使拟合效果达到最佳,选取4个相邻时刻,分别列出上述方程,最终方程组如下
(6)
其中,τ0、τ1、τ2、τ3是相继间隔Δt的4个时间点的信号传输时间。求解出k1、k2、k33个参数之后,通过拟合曲线可以得出τ0~τ3时段内任意时刻的信号传输时间。一组三阶多项式参数的有效范围为3Δt,可以根据接收机运动状态调整Δt,在算法执行效率和拟合精度方面作出取舍,得到适于系统运行的Δt。Δt设置的过大,会影响拟合效果,设置的过小,会加重系统负载,本文选取的Δt为0.05,拟合效果满足最终需求。关于任意时刻的传播时间计算可表示为
τ=τ0+k1(t-τ0)+k2(t-τ0)2+k3(t-τ0)3
(7)
其中,t为3Δt内的任意采样时刻,τ为t时刻的传输时间。结合式(4),即可模拟信号频率变化,实现信号的动态多普勒跟踪。
2.3 E1信号调制方式
由于Galileo E1频段与GPS L1频段中心频率相同,为了实现频带复用,Galileo系统在调制方式中引入了子载波,将频谱主瓣分裂至E1频点的两测,降低与GPS系统间的频谱干扰。E1频段基带信号采用CBOC调制,对数据通道与导频通道的两路信号进行时域相加,具体如图2所示。
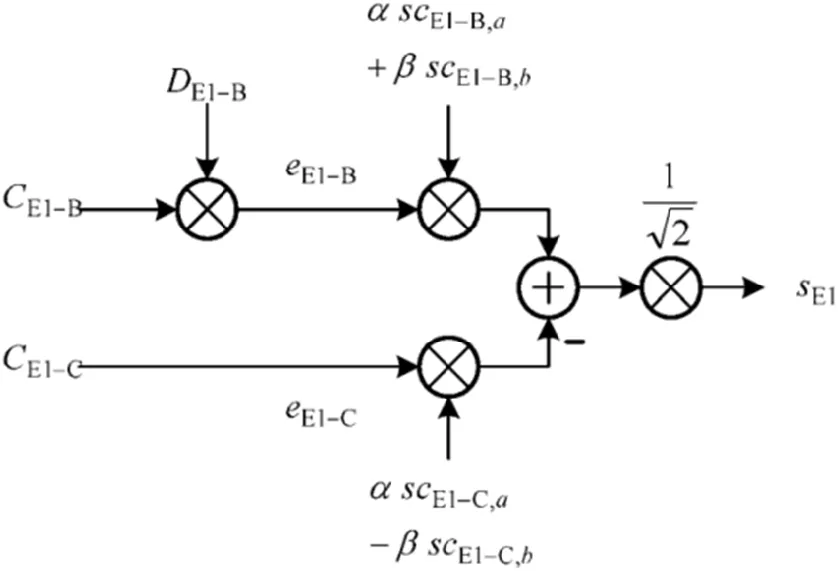
图2 E1频段CBOC调制

(8)
其中,scX(t)=sgn(sin(2πRs,Xt));RE1-B,a=RE1-C,a= 1.023 MHz;RE1-B,b=RE1-C,b= 6.138 MHz。
2.4 系统整体实现框图
Galileo E1频段信号模拟主要由两部分组成:信号生成和信号播放。信号生成部分完成Galileo中频信号文件产生,主要包含:(1)读取初始化参数,获取用户轨迹与时间信息;(2)判断可见星,根据Rinex星历参数生成模拟导航电文;(3)计算采样时刻信号传输时间,得出码相位与导航电文偏移;(4)结合调制方式与信号模型生成中频模拟信号;(5)为节省存储空间,加快模拟信号的生成速度,以2 bit量化、存储信号文件。
信号播放部分借助矢量信号发生器,通过FPGA编程实现[16]。AV1443矢量信号发生器是中国电子科技集团第41研究所提供的硬件平台,可产生频率范围为250 kHz~44 GHz的调制信号,拥有完善的人机交互页面,可实现信号参数以及硬件状态的动态设置,满足E1 信号播放要求。FPGA对中频信号的处理流程包含以下几个步骤:(1)对信号进行2 bit 到 16 bit 的数据映射,提高量化精度;(2)为了适配FPGA系统时钟,通过内插重采样滤波器实现对信号的采样率变换,将信号采样率提升至200 MHz;(3)将信号送入带通滤波器滤除带外干扰;(4)对信号进行D/A转换;(5)通过混频器,将信号频率搬移至E1频点。上述流程中,内插重采样滤波器是设计的重点和难点,本文采用Farrow滤波器实现信号的任意重采样,通过对相邻采样点进行线性内插实现任意点采样值估计,FIR子滤波器系数通过Matlab工具生成,系统整体实现框图如图3所示。

图3 系统整体实现框图
3 测试与验证
3.1 中频信号CBOC调制部分验证
为了验证Galileo中频模拟信号的正确性,对中频fIF=15 MHz,fs= 62 MHz的模拟信号进行功率谱密度分析,结果如图4所示。

图4 Galileo中频模拟信号功率谱密度曲线
CBOC调制是两路MBOC(6,1,1/11)调制信号的时域叠加,因此理论功率谱密度曲线与MBOC(6,1,1/11)相同。由图4中仿真结果可以看出,功率谱主瓣主要分布于中频fIF两侧,主瓣中心频率为fIF±1 MHz,且fIF±6 MHz频率位置有谱瓣突起,与MBOC(6,1,1/11)理论谱线完全吻合,说明E1信号CBOC调制的正确性,验证了Galileo中频信号的正确性。
3.2 射频信号验证
Galileo模拟信号经矢量信号发生器上变频至E1频段进行射频播放,通过UTREK410 GPS/Galileo双模接收机对生成的信号进行可行性验证。图5为UTREK410接收机显示的卫星捕获与跟踪状态,表明信号的动态多普勒拟合良好,可以实现信号的稳定捕获与跟踪,为最终的电文解调、位置解算奠定了基础。图6为UTREK410接收机显示的实时定位结果,定位结果显示的经纬度与模拟程序里给定的经纬度一致,时间与模拟的导航电文时间同步,位置稳定,不存在漂移,验证了Galileo E1信号模拟算法的准确性与可行性。

图5 UTREK410接收机实时卫星状态图

图6 UTREK410接收机定位结果
4 结束语
本文在推导了Galileo E1中频信号数学模型的基础上,分析了信号模拟涉及的关键技术,实现了动态多普勒的稳定跟踪,给出了系统实现流程框图。测试与验证部分从两个方面论证了信号模拟的正确性与可行性:(1)证明了中频模拟信号的功率谱密度与理论E1 CBOC调制信号功率谱密度曲线相符;(2)证明了射频输出信号可以被稳定跟踪,位置信息可以被正确解算,定位结果与设定坐标相符,无明显偏差。Galileo E1信号模拟源,灵活性好,可根据用户定义轨迹生成模拟信号,支持高动态设置,可以为Galileo硬软件接收机提供稳定的开发、测试环境。
[1] 张锐.Galileo卫星信号模拟器的研究[D].哈尔滨:哈尔滨工程大学,2007.
[2] 陈向东,高青,郭莉莉.卫星导航信号高精度模拟产生与控制技术[J].测绘科学技术学报, 2010,27(3):165-168.
[3] 李隽.卫星导航信号模拟器体系结构分析[J].无线电工程,2006(8):30-31,39.
[4] 陈颉,卢晓春,贺成艳.Galileo E1 OS信号捕获方法研究[J].时间频率学报,2013(4): 236-244,256.
[5] 史雨薇.Galileo E1信号性能分析与软件模拟源的设计[D].哈尔滨:哈尔滨工业大学,2012.
[6] 熊骏,宋茂忠,于巧稚.基于时间压扩的GPS信号多普勒算法实现与验证[J].航空兵器,2015(3):27-30,43.
[7] Julien O,Zheng B,Dong L,et al.A complete software-based IF GNSS signal generator for software receiver development[C].Long Beach:IONGNSS 17thInternational Technical Meeting of the Satellite Division,2004.
[8] Progress in Astronautics and Aeronautics.Global positioning system: theory and applications[M].USA:AIAA,2006.
[9] Lei D.IF GPS signal simulator development and verification[D].Alberta:University of Calgary,2003.
[10] 段远征.全球导航卫星系统测量中坐标转换研究[J].江苏科技信息,2016(30):62-64,68.
[11] Yao Yibin,Chen Peng,Zhang Shun,et al.A new ionospheric tomography model combining pixel-based and function-based models[J].Advances in Space Research,2013(4):89-95.
[12] Roncagliolo P A,Garcia J G.High dynamics and false lock resistant GNSS carrier tracking loops[C].CA,USA:Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation,ION GNSS,2007.
[13] European Union.The european GNSS (Galileo) open service signal in space interface control document[M].Swiss:European Union,2015.
[14] 刘松林. BOC调制扩频信号同步技术研究[D].哈尔滨:哈尔滨工程大学,2008.
[15] 李颖,赵风海,李金海,等. Galileo系统E1/E5/E6频段信号分析与仿真[J].计算机工程与设计,2014(2):368-375.
[16] 高春芳.基于DSP和FPGA的电子侦察信号模拟器设计[J].电子科技,2016,29(5):51-54.
[17] 高亮,宋茂忠.基于FPGA的北斗QPSK调制实现与解调验证[J].电子科技,2014,27(3): 95-98.

