基于ACO优化LS-SVM的变压器故障诊断

高国磊，李英娜，段效琛，李 川

(昆明理工大学 信息与自动化学院，云南 昆明 650500)

随着国民经济和我国电力工业的快速持续发展，社会上各行各业对电力的需求不断增加。近几年来，我国高压及特高压级别的变压器发生故障的频率越来越高，虽然我国在变压器监测与维修领域的技术有了明显提高，但是整体上仍有不足[1]。因此，加强变压器日常监测与维护，深入研究故障的预防性实验，才能有效提高对变压器各类故障的预防、修复能力。由此可见，使用合理有效的变压器故障诊断方法，对变压器状态的监测以及变压器故障诊断有着重要的实际意义[2]。

目前基于油中溶解气体分析技术(Dissolved Gases Analysis，DGA)的变压器故障诊断研究主要有传统诊断法和智能诊断法两类[3]。文献[4]采用入模糊理论来构造变压器状态诊断模型，存在编码涵盖范围小、不可扩展等不足。文献[5]建立了可增扩新规则的专家系统，提出可扩展的油中溶解气体成分的变压器故障诊断专家系统，但是训练样本少，分类准确率不高。文献[6]提出支持向量机、粗糙集和属性约简集选择的变压器故障诊断模型，但忽视了局部放电性故障。文献[7]提出利用微分进化优化神经网络,但是模型训练时间长，需要样本量大。

针对DGA技术在变压器故障诊断中的需求与应用，在分析传统故障诊断方法以及人工智能故障诊断方法存在不足的基础上，通过改进的核主元分析方法(Kernel Principal Component Analysis，KPCA)剔除异常离群值，利用蚁群算法(Ant Colony Optimization，ACO)优化参数，将最小二乘支持向量机(Least Squares Support Vector Machine，LS-SVM)引入变压器故障诊断中，对几种变压器故障进行分类。

1 变压器故障类型及特征气体的选取

由于变压器整体结构复杂，发生故障时往往是并发的故障，引起故障的原因也是多种多样的，很难根据某种数据判断故障的类型。变压器故障类型的划分有不同的标准，按照故障性质来分，可分为过热性故障和放电性故障[1]。

根据温度的范围不同，过热故障分为低温过热(150～300 ℃)、中温过热(300～700 ℃)和高温过热(700 ℃以上)3种类型。变压器的放电性故障是由高电应力引起的绝缘劣化，根据放电密度的不同分为局部放电、低能放电和高能放电[1]。不同的变压器故障产生气体种类如表1所示。

表1 变压器故障类型产气种类

由表1得出变压器故障的相关指数都跟溶解在变压器油中的气体组分和含量有着密切关系，因此利用油中气体和故障的映射关系来分析检测变压器的故障是可行的。方法研究对象为低温过热、中温过热、高温过热、局部放电、低能放电、高能放电这6个典型故障类型和正常状态，选取CH4、C2H4、C2H2、H2、C2H6这5种特征气体作为故障类型诊断的参量[8-9]。

2 蚁群优化最小二乘支持向量机方法

2.1 改进KPCA方法

传统的变压器故障分类方法在对数据进行特征提取的过程中，未考虑部分异常数据对提取过程的影响[10]。为了剔除部分异常数据，采用改进的KPCA方法进行特征提取后将故障样本数据输入分类器，能够输出较好的分类结果。引入特征空间信号重构的最小误差准则方法找出异常数据，降低异常数据对结果的影响。

假设故障样本数据为X={x1,x2,x3…xN}，设y=WTx，则有u=Wy作为原样本数据x的重构信号，即e=x-u，则样本数据的误差重构函数如式1所示：

(1)

由于误差重构函数优化的目的是在样本数据降维后尽可能降低信号损失，误差重构函数J(W)最小则意味着W等同于样本输入数据X的PCA子空间，即为X的主成分。因此，对误差函数的重构可以用来判断随机样本数据是否为离群值。

在此输入空间，给定阈值ε>0，用以判断识别空间异常值，如式2所示。

e(xi)=‖xi-WWTxi‖2>ε

(2)

样本数据集在经过KPCA非线性映射到高维空间后的数据集采用特征空间信号重构的最小误差准则判断是否出现异常值。高维空间数据集Φ(x)带入式(3)。

e(Φ(xi))=‖Φ(xi)-WWTΦ(xi)‖2

(3)

式(3)中，非线性函数Φ(xi)形式是未知的，不能直接进行误差重构[11]。将式(3)平方展开并引入核函数K(xi,xj)=Φ(xi)·Φ(xi)结果如式4所示。

e(Φ(xi))=Φ(xi)Φ(xi)-2WWTΦ(xi)Φ(xi)+
(WWT)(WWT)Φ(xi)Φ(xi)=K(xi,xi)-
2WWTK(xi,xi)+(WWT)K(xi,xi)

(4)

由此，改进的KPCA方法通过核函数求出重构误差大小并判断离群值。

2.2 最小二乘支持向量机

LS-SVM算法在保证分类精度的同时大大降低了计算复杂性，提高了求解效率[12]。在系统样本不充足的情况下，解决对非线性特征的样本数据优化难以达到全局最优和高维数的问题，因此在故障诊断方面应用广泛。

LS-SVM算法核心就是采用核函数的方法对样本空间进行数学上的投影，因此，选择合适的核函数直接影响了LS-SVM算法的优劣[13]。定义核函数K(x,xi)=Φ(x),…,Φ(xi)：如果存在从Rn到Hilbert空间H的变换

(5)

K(x,x′)=[φ(x)·φ(x)′]

(6)

式(6)中，[φ(x)·φ(x)′]表示空间中内积，则称Rn×Rn上的函数K(x,x′)是核函数。高斯径向基核函数

K(x,xi)=exp(-‖x-xi‖2)/2σ2

(7)

式(7)中，x是输入向量，x′是第i个RBF函数的中心，这里x和x′有相同的维数；σ是常数，表示RBF函数围绕中心点的宽度。高斯径向基核函数具有将原始空间映射为无穷维空间的特点，从而使它成为目前应用最多的核函数。

2.3 ACO优化参数

ACO是一种全局优化的算法[14-15]。它的基本思想：设置两组蚁群，一组对核函数参数σ寻优，另一组对惩罚系数C寻优。每只蚂蚁选择路径的同时利用式8对信息素进行更新，再对两组蚂蚁计算其目标函数值，得出此次迭代的最小函数值。然后在获得函数值最小的路径上按照式9增加信息素，这样就完成了一次循环。重复上述步骤，直到满足设定的结束条件。最后从每次迭代的最小值中选出最小的函数值，以及此时的σ和C即为所求参数。当蚂蚁遍历完所有的城市后，各城市之间线路上的信息素浓度为

(8)

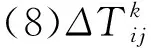
(9)

式9中，Q为信息素常数，代表每只蚂蚁完成遍历释放的信息素总量；Lk为蚂蚁k到达所有城市后所经过的线路总长度。

2.4 基于蚁群优化最小二乘支持向量机方法

蚁群优化与最小二乘支持向量机方法(ACO-LSSVM)的具体步骤如下：

(1)初始化数据。首先利用改进的KCPA特征提取方法剔除样本中的异常数据，然后对故障样本进行归一化预处理；

(2)初始化参数。设置蚁群算法的初始信息素、信息素蒸发系数、信息素重要程度参数、随机路径选择路径的概率；

(3)路径选择。用式8对路径信息素进行更新，每只蚂蚁完成一次路径选择后解码该路径，得到两组自变量值，将这两个值带入交叉验证的LS-SVM模型中，得到目标函数。再对两组蚂蚁计算其目标函数值，得出此次迭代的最小函数值；

(4)获得函数值最小的路径。用式(9)增加信息素，这样就完成了一次循环。如果当前的迭代次数满足最大的函数评估次数或者算法在迭代中没有任何改善时，则停止迭代，输出最优解，否则。转到步骤(3)；

(5)获取此次最优的LS-SVM的核函数参数σ以及惩罚系数C；

(6)将已经选取好的训练样本集和经交叉验证得到的σ、C一起训练并优化一对已组合分类的LS-SVM模型；

(7)重复步骤(6)直至模型满足精度要求，得到ACO-LSSVM模型；

(8)最后用测试样本集验证诊断的准确性。

3 变压器故障诊断实例分析

3.1 样本数据预处理

实验DGA样本集中共有165个样本数据，选取110组样本数据作为训练样本集，55组样本数据作为测试样本集。首先利用的改进KPCA特征提取方法，剔除这165组故障样本数据中的异常数据，发现该故障样本中第155行高温过热故障数据是异常数据，有3个特征变量的值出现异常。

由于变压器油中特征气体的浓度含量的数量级差异性很大，直接将特征气体含量作为模型的输入会导致诊断结果不准确。经过归一化处理之后，数据样本分布在[0,1]空间内，作为模型的输入特征向量。

3.2 蚁群优化LS-SVM算法实现变压器故障分类

实验采用110组训练样本集和55组测试样本集对蚁群优化最小二乘支持向量机的变压器故障诊断模型的故障分类准确率进行实验。

首先使用改进的KPCA算法对故障样本的异常数据进行剔除，再将数据进行归一化得到五种特征气体体积含量占总气体体积含量的百分比，将蚁群算法优化得到的两个LS-SVM的参数：核函数参数σ2=1.238以及惩罚系数C=4.074，带入ACO-LSSVM模型，得到故障分类的效果如图1所示。

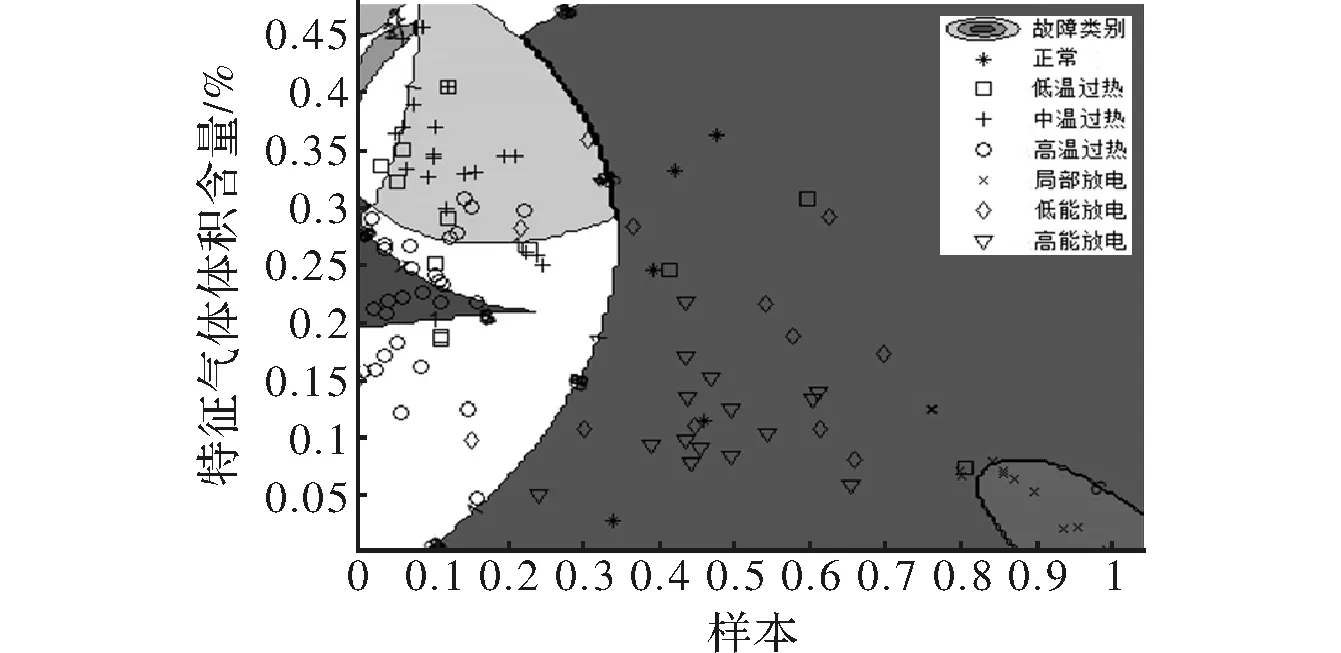
图1 ACO-LSSVM中故障样本分类效果

使用改进的KPCA算法对故障样本的异常数据进行剔除，再将数据进行归一化得到5种特征气体体积含量占总气体体积含量的百分比，未经蚁群优化LS-SVM的参数，计算得到核函数参数σ2=1.138 3以及C=1.802 1，带入LS-SVM模型，得到故障分类的效果如图2 所示。

表2 故障样本错误分类 μL/L

图2 LS-SVM中故障样本分类效果

模型故障类型样本总数ACO-LSSVM分类错误样本数LS-SVM分类错误样本数总体正确率/%ACO-LSSVM低温过热51192.57LS-SVM中温过热80283.14高温过热1313局部放电600低能放电710高能放电1015正常500

观察表2和表3，针对实验收集的165组故障样本数据经过异常数据剔除后进行不断的训练，得出变压器正常运行状态和6种典型的变压器故障类型的分类情况。ACO-LSSVM模型得到的变压器故障分类准确率比LS-SVM模型得到的变压器故障分类准确率提高了9.43%。

4 结束语

改进的KPCA方法剔除异常数据，并引入ACO优化LS-SVM参数对变压器进行的故障诊断研究。结果表明：该模型以变压器油中溶解的各种气体产气量为评价指标，经过训练的ACO-LSSVM模型能对变压器故障数据样本进行正确分类，总体准确率为92.57%，分类准确性和有效性明显优于LS-SVM方法，为变压器故障检测提供了依据。

[1] 国家电网公司运维检修部.变压器类设备典型故障案例汇编:2006-2010年[M].北京:中国电力出版社,2012.

[2] 张远博.油纸绝缘变压器局部放电产气特征的模拟研究[D].哈尔滨:哈尔滨理工大学,2013.

[3] Gao W,Bai C,Liu T.A dynamic integrated fault diagnosis method for power transformers[J].The Scientific World Journal,2015(7):459268-45977.

[4] 焦振毅,任建文,陈鹏.基于模糊理论的变压器故障诊断模型研究[J].电力科学与工程,2012,28(6):39-43.

[5] 师瑞峰,史永锋,牟军,等.油中溶解气体电力变压器故障诊断专家系统[J].电力系统及其自动化学报,2014,26(12):49-54.

[6] 吴立帅,葛玻,宋书中.基于粗糙集与支持向量机的变压器故障诊断[J].电源技术,2014,38(4):768-770.

[7] 刘卓,黄纯,李波.利用微分进化优化神经网络的变压器故障诊断[J].电力系统及其自动化学报,2011,23(2):54-58.

[8] 王健一,李金忠,凌愍,等.新版电力行业标准《变压器油中溶解气体分析判断导则》解读[J]. 变压器,2014,51(12):49-53.

[9] Alamuru V.Hybrid diagnosing techniques for analyzing dissolved gases in power transformers[J].IEEE Transactions on Computer Scienc,2015,7(2):32-43.

[10] 杨廷方,张航,黄立滨,等.基于改进型主成分分析的电力变压器潜伏性故障诊断[J].电力自动化设备,2015,35(6):149-153.

[11] 唐勇波.改进特征样本方法的KPCA变压器故障检测模型[J].计算机工程与应用,2014, 50(21):4-7.

[12] Kisi O.Least squares support vector machine for modeling daily reference evapotranspiration[J]. Irrigation Science,2013,31(4):611-619.

[13] 王逸萍.基于最小二乘支持向量机的变压器故障诊断[J].电工电气,2016(6):24-27.

[14] 邓玉梅.基于蚁群优化的BP神经网络目标威胁估计方法[J].电子科技,2016,29(7):33-35.

[15] 杜博,夏春蕾,戴曙光.融合改进蚁群和粒子群算法的路径搜索应用[J].电子科技,2016, 29(9):4-6.