基于改进的LVQ神经网络图像边缘提取研究
郎 俊,白国振,周 媛
(上海理工大学 机械工程学院,上海 200093)
图像边缘检测算法的研究一直是图像处理方面的重点关注对象。相对于传统的边缘检测算子,人工神经网络对于处理复杂的环境信息、模糊的背景知识和推理规则的分类具有较好的优越性。因而用神经网络实现边缘特征的分类,从而实现图像的边缘检测的方法引起了人们的关注。文献[1]提出一种四元数和自组织神经网络(SOM)相结合的边缘检测算法,该算法提取的轮廓还保留有部分噪声[1]。文献[2]提出一种神经网络与模糊算法相结合的检测方法[2],文献[3~4]提出了利用PCA结合LVQ的方式实现目标物体的分类[3-4],文献[5]提出一种相似性度量函数,判断特征的相似度[5],文献[6]利用遗传算法实现初始值优化[6]。
本文通过图像中像素的中值特征向量、方向信息特征向量和Krish算子方向特征向量构建像素的特征向量(3×1的输入矩阵),作为神经网络的输入,再利用改进的GLVQ神经网络(MGLVQ)对图像中的像素进行分类,实现目标边缘轮廓的提取。
1 GLVQ神经网络
设有一组n个样本,特征空间为p维,即x∈Rp其分布密度f(x)是不随时间变化的。用i表示获胜单元(最佳匹配单元)的标号,定义如式(1)所示,损失函数以衡量获胜神经元权值与输入向量x之间的欧式距离的误差值(c为类别数)。
(1)
式中uir是一组权重,在竞争层神经元权值的学习过程中,每次权值wr的更新,由隶属度函数ur根据输入向量X定义每个神经元损失函数的值,从而使得每个神经元的权值更新值不同。损失函数往往对获胜神经元有所限定,是对于输入向量X的获胜神经元的权值,即与输入向量X的欧式距离最小,其隶属度函数定义如式(2)所示[7]。
(2)
其主要目的是找到c个中心wr,使得损失函数LX的期望值E(W)达到最小。
(3)
当f(x)未知时,使用LX在样本上的均值R(W)代替E(W),如式(4)所示。
(4)
为使均值R(W)达到最小,采用梯度下降法解决该寻优问题,此时用在每一样本上的局部梯度作为修正的方向[8]。对LX作必要的数学推导如式(5)。

(5)
求梯度时分两种情况:对于获胜单元其梯度如式(6)所示。
(6)
(7)
对于其他单元Vj(j≠i)时,其梯度如式(8)所示。
(8)
把式(5)和式(7)代入权值学习策略中得出如式(8)和式(9)的权值更新规则。

(9)
(10)
竞争层神经元的初值对GLVQ算法的最后收敛结果无影响,在GLVQ权值的学习过程中,每次输入向量X,会对竞争层每个神经元的权值进行更新,使得各个神经元的数据充分利用[9-10]。GLVQ神经网络对获胜神经元的学习具有好的性能,但对于其他神经元的学习性能不稳定,从而在实践中的分类效果不理想。针对该问题提出如下的改进算法。
2 基于GLVQ算法的改进(MGLVQ)
2.1 损失函数选取
A.I.Gonzalez和M.Graiia[11]提出对于GLVQ神经网络,集群和输入向量空间的大小对其聚类效果有着很大的影响,而损失函数的选取则是导致这种不理想结果的主要原因。
为了体现出获胜神经元与失败神经元的欧式距离的关系,在本算法中的采用获胜神经元与失败神经元的欧式距离比值,作为该神经元损失函数的自变量如式(11)所示。
(11)
Karayiannis 和 Pai 提出了隶属度函数的选用规则[12]。(1)整个数据集的比例不变;(2)获胜神经元的隶属度函数值为1;(3)非获胜神经元的隶属度函数值在0~1之间;(4)如果该是非获胜神经元并且其与输入向量的欧式距离很大,则其隶属度函数值趋于0。利用这些规则定义的隶属度函数确定竞争层神经元的权重更新差值,可以提高竞争学习矢量化算法的稳定性。
(13)
则0 (13) (14) 对获胜神经元,损失函数梯度为 (15) 对未获胜的神经元,损失函数梯度为 ΔvL(wj)=-2(x-wj)N2exp(-N) (16) 由于GLVQ神经网络的权值初值对其最终收敛结果无影响,所以在使用GLVQ神经网络进行分类时,一般采用随机值或样本均值作为权值初始值。MGLVQ对于其初值比较敏感,所以为了得到合适的初值,需要对初值进行寻优[13]。人工鱼群算法由于其有较快的收敛速度,在精度要求不高的情况下,可使用它快速得到可行解,所以在本文中选用人工鱼群优化算法对其初值进行寻优[14-15]。 将人工鱼群算法用于连续空间向量的数据分类时,需要对人工鱼进行编码、人工鱼之间的距离及其邻居、和聚类中心的定义。在算法中人工鱼编码直观的表现出了具体的参数信息,定义Fish(x1,x2,x3,C)为人工鱼编码,其中x1,x2,x3为人工鱼的特征属性,其具体编码形式见表1,C为其类别属性,C的取值为1或0。 表1 人工鱼编码 两个人工鱼之间的距离表示着两者的特征差异,参照LVQ神经网络中竞争层神经元与权值之间的特征比较,人工鱼之间的距离采用欧式距离表示,如式(17)所示。 (17) 其中,i,j示两个不同的人工鱼,xik-max表示第i个人工鱼的第k个特征属性的上界;xik-min表示第i个人工鱼的第k个特征属性的下界。 通过欧式距离定义人工鱼的邻域 n(i,f)={r|d(i,r) (18) 其中r代表邻域内的其他个体;f代表邻域距离;G代表整个鱼群。 聚类中心采用人工鱼聚群的中心位置,在该算法中分别取所有人工鱼的特征值上下界的平均值。 (19) n代表人工鱼聚群中的人工鱼数目[12-14]。其中适应度函数定义如式(20)所示 F(x)=a×s+(1-a)×k (20) 其中系数a取值(0,1),s表示正确分类的个体数目占种群中个体总数的比例,k表示一条规则能将个体正确分类的概率。 (1)给定一组未标号的数据X={x1,x2,…,xn},类别数c,迭代次数T,允许误差ε; (2)对人工鱼进行编码生成初始鱼群,通过数据采样提取鱼群的训练数据集; (3)设置鱼群的类别、步长以及可视范围,并使鱼群通过觅食、追尾、聚群等行为获取权值初始值; (4)根据适应度函数计算其适应度值,进行规则评价,如果不满足终止条件,则继续进行觅食、追尾、聚群等行为,最终获得权值初始值W0; (5)对t=1,2,…,T,初始学习步长a0计算 (21) 对于K=1,2,…,n,找出满足式(22)的神经元权值。 ‖xk-wi,t‖=min{‖xk-wi,t-1‖} (22) 通过式(23)和式(24)修正所有权向量{wr,t}。 获胜神经元权值修正 (23) 未获胜神经元权值修正 wr,t=wr,t-1+at(x-wi)N2(exp(-N)]),r≠i (24) (6)通过式(25)计算权值的学习前后误差。 (25) 若式(25)中计算得Et小于阈值则停止;否则,对下一个t重新计算,直到满足条件; (7)通过步骤5得到合适的权值之后,计算最近标本下对输入向量X进行c种划分。获胜神经元对应向量值为1,其余为0。 (26) 图1 边缘检测流程图 图像的边缘点是图像中灰度突变的像素点,相比于噪声点,边缘点邻域的灰度分布具有一定的特性,灰度值的突变具有方向性,灰度突变的像素在图像中有一定的连续性。根据边缘点邻域的中值特征向量、方向信息特征向量、Krish算子方向特征向量构建神经网络的输入特征向量。 采用Robel算子对图像进行边缘提取,以作为神经网络教师图像,在教师图像图任意选取600个训练样本,边缘点和非边缘点的比例为1:1,MGLVQ的主要结构是3个输入神经元,4个隐含层神经元,2个输出神经元,初始学习步长 为0.1。实验采用经典Lena灰度图像作为测试图像,图3是经典LVQ神经网络对其的边缘提取,图4为GLVQ神经网络的边缘提取效果,图5为MGLVQ的边缘提取图像。从图3中可以看出,经典LVQ神经网络的边缘提取中存在边缘断裂、边缘缺失等问题,而GLVQ神经网络图像噪声较多,使其边缘提取效果不理想。如图5所示,MALVQ神经网络即保证了边缘的连续性,也大量减少了图像中的噪声,使得边缘提取的效果更好。 图2 灰度图像 图3 LVQ神经网络 图4 GLVQ神经网络 图5 MALVQ神经网络 表2中是对图4和图5的图像边缘点统计,原图中共有65 536个像素,GLVQ神经网络提取了29 545个边缘点,MGLVQ提取18 727个边缘点,各占总像素比例的45.08%和28.58%。 表2 分类比例 表3为实验结果中GLVQ神经网络和改进算法的权值初始值和训练结束后聚类中心的对比。其中GLVQ初始值是由样本均值得到,MGLVQ的初值是通过人工鱼群算法寻优而得。 表3 神经网络权值 实验结果表明,MGLVQ不会出现对图像边缘过度提取的情况,从而使得边缘提取能够更好的保持边缘细节,同时减少图像噪声对边缘的影响,增强了对其边缘检测的稳定性,能够得到较为理想的图像轮廓。 (1)针对GLVQ神经网络损失函数的隶属度函数不能应出获胜神经元与失败神经元的欧式距离之间的关系,提出了改进的隶属度函数,并通过人工鱼群算法对神经网络权值进行离线细调,之后再通过梯度寻优算法对权值进行在线细调; (2)从仿真分析可知,MGLVQ神经网络在去除噪声方面明显优于GLVQ,同时针对GLVQ神经网络出现次数较多的错误分类(像素分类明显不合理),使得图像不能实现正确边缘提取的情况。而MGLVQ神经网络能够实现更加准确的分类,轮廓图像中不存在大面积的白色区域。综上,MGLVQ神经网络比GLVQ神经网络拥有更好的图像边缘细节提取能力,能够得到质量更好的边缘轮廓图像; (3)实验证明MGLVQ在像素分类上,与GLVQ和LVQ神经网路相比,MGLVQ能够获取比较完整的图像轮廓,其在分类作用上效果显著。所以MGLVQ神经网络可以作为一种分类算法应用于人工智能、模式识别等领域。 [1] 王铮,李兴民.基于四元数和SOM神经网络的彩色图像边缘检测[J].计算机应用,2012,32(2):510-513. [2] 贾超,邹琪,姚芳,等.基于神经网络与模糊算法图像边缘检测方法[J].计算机应用研究,2008,25(11):3507-3508. [3] 胡帅,顾艳,曲巍巍.基于PCA-LVQ神经网络的教学质量评价模型研究[J].河南科学,2015(7):1247-1252. [4] 胡红,曾恒英,梁海波,等.基于主成分分析和学习矢量化的神经网络岩性识别方法[J].测井技术,2015,39(5):586-590. [5] 胡耀民,刘伟铭.面向特征数据范围的泛化LVQ算法[J].模式识别与人工智能,2013,26(8):761-768. [6] 马利克,彭进业,冯晓毅.遗传算法优化LVQ网络的监控视频关键帧内容识别[J].西北大学学报:自然科学版,2015,45(4):573-578. [7] Iwata H,Agui T,Nagahashi H.Boundary detection of color images using neural networks[J]. IEEE International Conference on Neural Networks,1995,3(1):1426-1431. [8] Uchiyama Y,Haseyama M,Kitajima H.Hopfield neural networks for edge detection[J].Circuits and Systems,2001,3(1):1012-1018. [9] 闫德勤,迟忠先,王军.MLVQ网络聚类算法[J]. 自动化学报,2004,30(4):608-612. [10] 张志华,郑南宁,王天树.广义LVQ神经网络的性能分析及其改进[J].自动化学报,1999,25(5):583-589. [11] Gonzalez A I,Graiia M,D’Anjou A.An analysis of the GLVQ algorithm[J].IEEE Transactions on Neural Networks,1995,6(4):1012-1026. [12] Nicolaos B Karayiannis,PinI Pai.Fuzzy algorithms for learning vector quantization[J].IEEE Transactions on Neural Networks,1996,7(5):1196-1210. [13] 戴上平,姬盈利,王华,等.基于多群协同人工鱼群算法的分类规则提取算法[J].计算机应用研究,2012,29(5):1675-1679. [14] 廖胜娟.基于人工鱼群算法的MES车间动态调度问题研究[J].电子科技,2014,27(10):64-66. [15] 李家森,席志红,赵彦青.北斗/INS组合导航中人工鱼群粒子滤波的应用[J].电子科技,2013,26(6):157-161.2.2 鱼群算法寻优获取权值初值


2.3 MGLVQ算法步骤
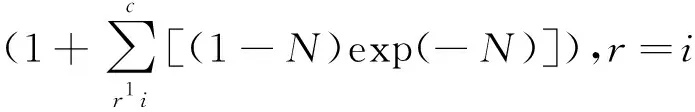

3 实验及分析






4 结束语

