导弹复合控制系统的自适应控制器设计*

刘 凯 ，宋晓娜 ，2，刘跃敏 ，李东山

（1.河南科技大学信息工程学院，河南 洛阳 471023；2.中国空空导弹研究院，河南 洛阳 471009）

0 引言

随着科技的不断发展，常规气动力导弹已经很难满足现代复杂的作战环境。因此，新式导弹通常采用直/气复合控制的方法，来实现高精度制导的作战要求。在导弹控制系统中，直接力的引用，在提高导弹控制系统过载能力的同时，也使得制导过程变得更加复杂，为控制器的设计带来了更大的挑战。针对直/气复合模型，国内外研究人员已经做出了很多的研究工作，其中美国的PAC-3和法国的Aster-30都已经实现了弹体与目标直接碰撞的实验［1-2］。

实验证明现代导弹采用的复合控制模型与传统气动力制导相比，具有过载能力大，且响应速度不受大气层内空气密度的限制，是实现导弹全空域“趋零脱靶量”的一种有效技术［3］。因此，很多研究学者针对导弹复合控制系统进行了各类问题的探索研究，其中文献［4］针对导弹复合控制系统中侧喷流干扰较大的特点，通过运用自适应遗传算法等理论，提出了一种不依赖精确数学模型的智能控制算法。文献［5］针对模型的不确定性和大气环境的干扰，提出了气动子系统的自适应滑模控制方法。文献［6］为保证导弹在气动参数变化的情况下，控制系统仍能够有较好的动态跟踪性能，提出了一种参数自适应滑模控制方法。文献［7］研究了导弹初始迅速大转弯的问题，且给出了稳定性的设计方法。文献［8］为了提高直接力控制的使用效率，采用模糊控制方法对导弹脉冲发动机的点火逻辑进行了设计。文献［9］提出了一种基于非线性干扰观察器的增强型滑模控制方法，该方法与传统的滑模控制方法相比有很好的鲁棒性，但设计过程过于复杂，计算量偏大。

本文采用自适应滑模控制，针对导弹复合控制系统，建立纵向动态化模型，做出适当的优化设计。对气动力采用滑模控制的方法进行研究，并用自适应控制理论对系统进一步优化，同时采用模糊控制对直接力部分进行设计，节省脉冲发动机燃料的使用，提高导弹的制导精度。

1 复合控制系统的数学模型

考虑到在末节制导过程中，导弹的主推发动机已经停止，并且末节制导所消耗的时间非常短，所以可以将弹体的质量m和速度v设定为常值，建立如下导弹动力学模型：

其中，α为攻角，ωz为俯仰角速度，m为弹体的质量，v为导弹速度，ai（i=1，…，5）为弹体动力学参数，式中为固体发动机到弹体质心的距离。由于的数值非常小，即系统为若非最小相位的系统［10］，因此，经过适当变换后得到导弹数学模型为：

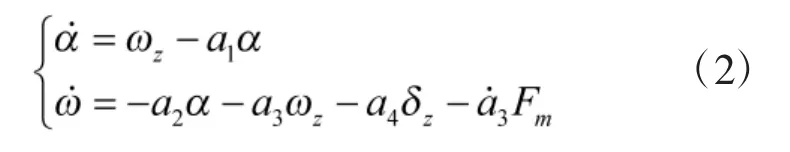
2 直接力/气动力复合控制方案

复合控制系统由直接力和气动力两部分组成，其中以气动力设计为基础，保证导弹飞行中的稳定性，消除复合控制产生的耦合效应，提高控制系统的鲁棒性。而直接力控制的目的是增加导弹的过载能力，减小系统的响应时间。直接力/气动力复合控制系统的结构图如图1所示。

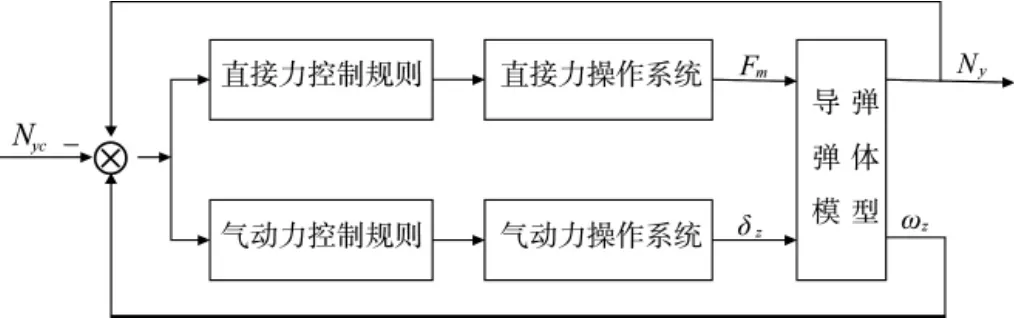
图1 直接力/气动力复合控制系统结构图

2.1 气动力控制方案

气动力控制系统设计，采用自适应滑模变结构控制方法［12］，来增加复合控制系统的稳定性，减少不确定干扰对制导系统的影响，同时由于过载可以通过测量得到，因此，可以将式（1）和式（2）变换后得到：

设过载指令为Nyc，目的是确定合适的输出指令Ny，能够跟踪期望过载Nyc，令过载跟踪误差为e=Ny-Nyc，则可以通过设计适当的控制律δz，能够使得。

选取切换面为：

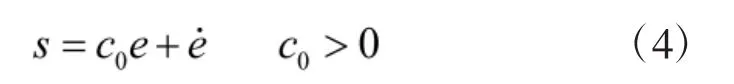
对式（4）两边求导可得：

为了保证在有限时间内到达切换面，采用指数趋近律；

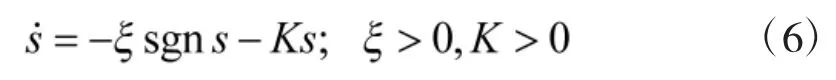
将式（5）与式（6）联立可得

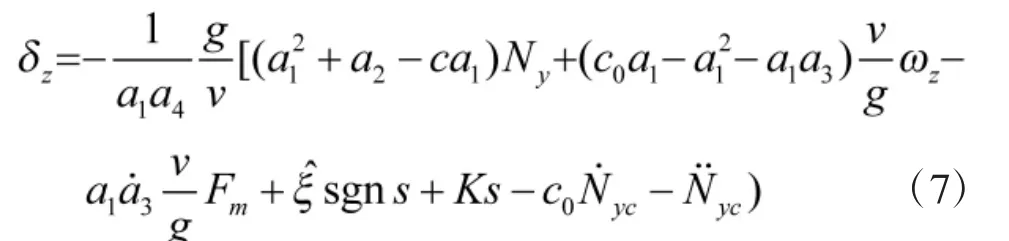
为了避免滑模控制引起的抖动问题，采用自适应控制理论对ξ进行估计，为估计值，可以由自适应算法式（8）得到

证明：取李雅普诺夫函数为：

式中，为估计值误差，且。

将式（9）两边求导得：

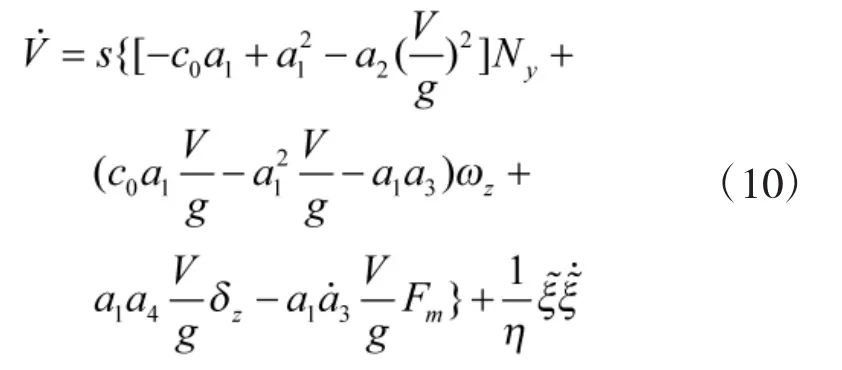
将式（7）带入式（10）中可得：

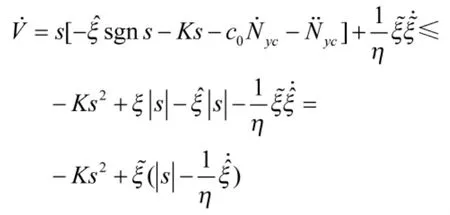
由式（8）可得：

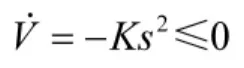
则复合控制系统渐进稳定，系统内所有值在设计范围内有界，证毕。

2.2 直接力控制设计

取直接力切换控制为：

由于在滑模控制的切换项中，符号函数sgn（·）在一定程度上会引起系统的抖振，影响系统的稳定行，因此，采用连续函数s/|s|+γ来替换符号函数sgn（·）的方法，减少系统抖振问题，则可以得到：

其中，γ为引入的一个小量，目的是为了提高直接力的使用效率，接下来采用模糊控制的方法对γ进行设计。

从复合控制系统的过载响应可以看出，过载误差e=Ny-Nyc，能够反映复合控制系统的指令跟踪性能。在此，把e=Ny-Nyc和作为模糊控制的输入，γ为模糊控制的输出，模糊控制集为：

{NB（负大），NM（负小），ZO（零），PM（正小），PB（正大）}

其中，输入e，和输出γ采用三角函数作为隶属度函数，输出γ如图2所示。

在复合控制系统中，过载误差e反映了系统的跟踪精度，如果误差e=Ny-Nyc为PB，此时需要设定较大的直接力控制量，来减少这种趋势。另外，如果过载误差变化律为PB或PM，则误差仍然在变大，也应增强直接力的控制，所以将γ设置为PB，同理，如果为NB或NM说明，误差在逐渐变小，不需要在加强直接力Fm的控制量，可以将γ设置为PM；若e为PM，则γ为NM或NB，若误差变化律为ZO，则不需要改变直接力控制量，这时γ应选择ZO。

图2 模糊输出隶属函数

表1 模糊控制规则表

进一步分析可知，当取值过大时需要更多的固体发动机提供推力，这样一方面会降低脉冲发动机的使用效率。另外一方面，会加大复合控制系统的不稳定性。因此，为了提高系统的响应速度，保证复合控制的精度取关于的函数；

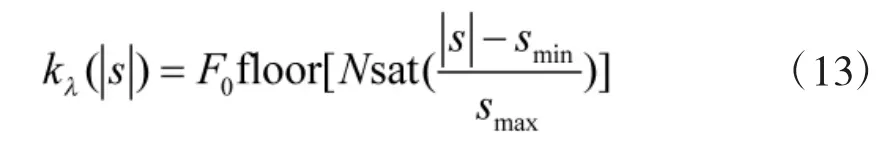
整理后可得：

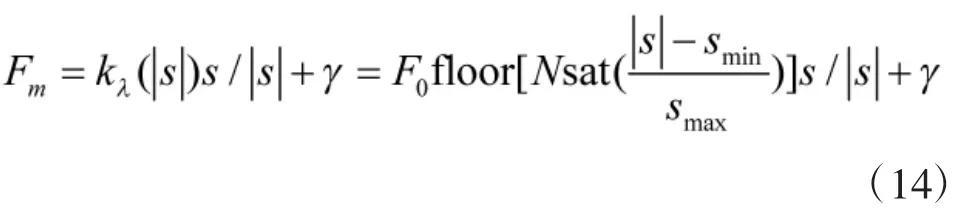
到此，直接力控制系统设计完毕。

3 仿真结果

本文采用MATLAB软件对导弹复合控制器进行仿真分析，首先针对式（3）数学模型

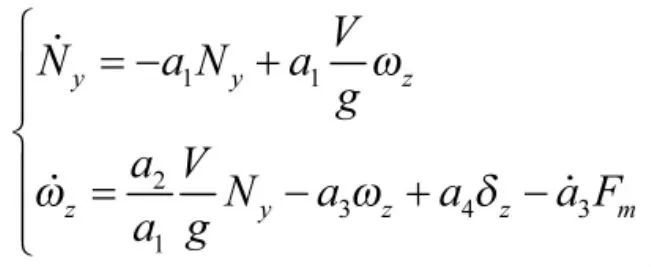
选取导弹末节速度为V=1000 m/s，g=10 m/s2，固体发动机最大推力值为F0=5000 N，直接力的动态工作时间 =0.005 s，固体发动机到弹体质心距离为l=1 m。其次，复合控制器中k=-15，N=5，Smin=2.0，Smax=10.0，过载指令Ny=25。为了验证加入自适应模糊滑模控制的效果，选取正弦函数作为直接力输入信号，与自适应模糊滑膜控制作对比，仿真结果如图3～图5所示。其中虚线部分为滑膜控制响应，实线部分为自适应模糊滑模控制响应曲线。

最后，由于在制导过程中直接力的开启与关闭，对导弹的飞行姿态产生很大的影响，因此，把固体发动机的开与关作为扰动输入，选取正弦函数来实现。由图6可知，制导指令发出后，由固体发动机的开与关和滑膜控制引起的扰动，使得复合控制系统在跟踪过载指令过程中会引起一定的抖动。而采用自适应模糊滑膜控制方法，使复合控制系统的性能大幅地提高，系统能够快速跟踪过载指令，且能够有效避免复合控制系统的抖动问题。

通过上述仿真结果可以清晰看出，所设计的复合控制器，对系统给出的过载指令具有很好的跟踪效果，自适应模糊控制的采用，有效地提高了控制系统的稳定性，同时，直接力的引入大幅缩短了系统的响应时间，提高了制导的精度。

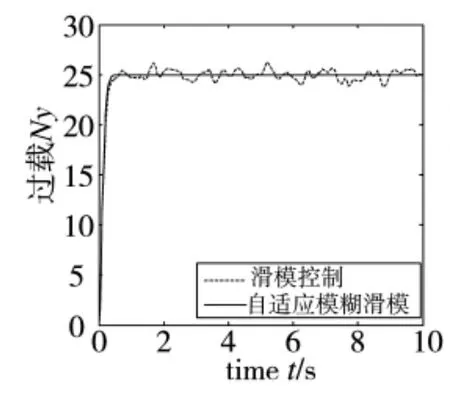
图3 过载跟踪响应

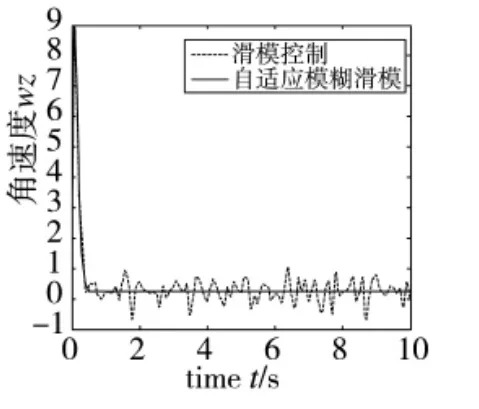
图4 俯仰角速度响应

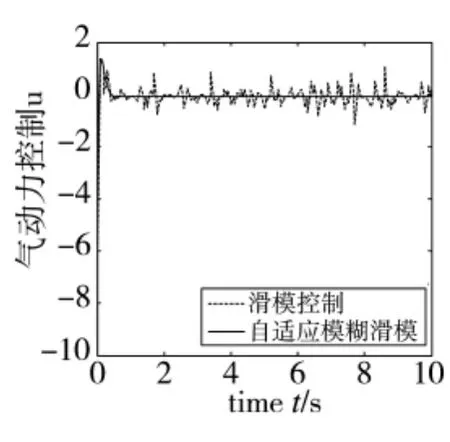
图5 气动力控制

图6 固体发动机消耗个数

4 结论

本文针对姿控式复合控制系统进行了研究，首先对其数学模型进行了适当的调整，在此基础上，运用滑模控制理论对气动力部分进行了设计，并采用自适应控制理论对其进行了参数优化。其次，进一步采用模糊控制理论方法，对直接力部分进行设计。最后对所设计的导弹复合控制器，进行了仿真验证，从仿真结果中可以清晰地看出，通过对控制系统的合理分配，可以在保证系统稳定的同时，提高系统响应速度以及发动机的使用效率。

［1］王晖娟.美国陆军下一代PAC-3导弹成功拦截靶弹［J］.战术导弹技术，2011，32（3）：37-37.

［2］储蔚，野舟.PAC-3导弹拦截巡航导弹目标试验获得成功［J］.飞航导弹，2012，42（5）：1-1.

［3］雷虎民，张旭，董飞垚，等.零控脱靶量有限时间收敛制导律［J］.国防科技大学学报，2015，37（3）：136-141.

［4］史震，马文桥，王飞，等.直接力/气动力复合控制导弹智能控制算法 ［J］.南京理工大学学报，2014，38（4）：481-489.

［5］邵雷，雷虎民，赵宗宝，等.直接侧向力/气动力复合控制影响因素研究［J］.飞行力学，2015，33（1）：57-60.

［6］WEI M，RUI S，HONG Y，et al.Adaptive sliding mode BTT autopilot for cruise missiles with variable-swept wings［J］.哈尔滨工业大学学报（英文版），2014，21（2）：33-42.

［7］李稀媛，敖百强，赵明元.导弹初始大角度转弯复合控制研究［J］.现代防御技术，2014，42（5）：65-69.

［8］滕江川，吴晓燕，陈永兴，等.基于模糊控制理论的脉冲推力器点火算法［J］.四川大学学报（工程科学版），2011（s1）：194-198.

［9］LEE H，HUANG X，YIN H.Enhanced sliding mode control for missile autopilot based on nonlinear disturbance observer［C］//International Joint Conference on Computational Sciences and Optimization，IEEE，2009：210-213.

［10］王明东，季田，刘宪林.非最小相位系统的灰色去余控制［J］.控制工程，2013，20（6）：1074-1076.

［11］廖海波.基于反演法的某制导迫弹鲁棒自适应控制器设计［J］.兵器装备工程学报，2016，37（5）：70-73.

［12］ZHAO F，UTKIN V I.Brief paper：adaptive simulation and control of variable-structure control systems in sliding regimes［J］.Automatica，1995，32（7）：1037-1042.

［13］朱 枫，韩晓明.地空导弹战场适应能力评估研究［J］.火力与指挥控制，2016，41（9）：74-79.