基于熵权的航空装备维修费用军事效益评估方法*
陈盖凯,张红斌,赵高峰,杨新广
(1.空军西安飞行学院,西安 710306;2.解放军93066部队,黑龙江 牡丹江 157000)
1 维修费用军事效益评估概念
维修费用军事效益,是维修费用支出所取得的军事成果与维修费用投入量的比较。维修军事成果是指在规定的条件下,完成既定的维修任务,达到规定的维修质量要求,实现既定的维修效率,可表现为物质形式和价值形式。物质形式是指维修后装备完好数量的增加和性能的提高,价值形式是指维修保障能力或部队战斗力的提升[1]。维修费用军事效益可用下式表示:
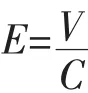
式中,E为维修费用的军事效益;V为维修费用的军事成果;C为维修费用支出。
在取得相同维修费用军事成果的情况下,维修费用支出越少,军事效益越高;在维修费用支出一定的情况下,维修费用军事成果越多,军事效益越高。因此,只需计算维修费用的军事成果,就可以对航空装备维修费用军事效益进行评估。
2 维修费用军事成果评估指标体系
由于维修费用的投入能够提高维修人员技术水平、增强维修保障能力、增加航空装备完好数量,最终提高部队战斗力。依据战斗力的量的规定性和质的规定性,可以建立维修费用军事成果评估指标体系如图1所示。
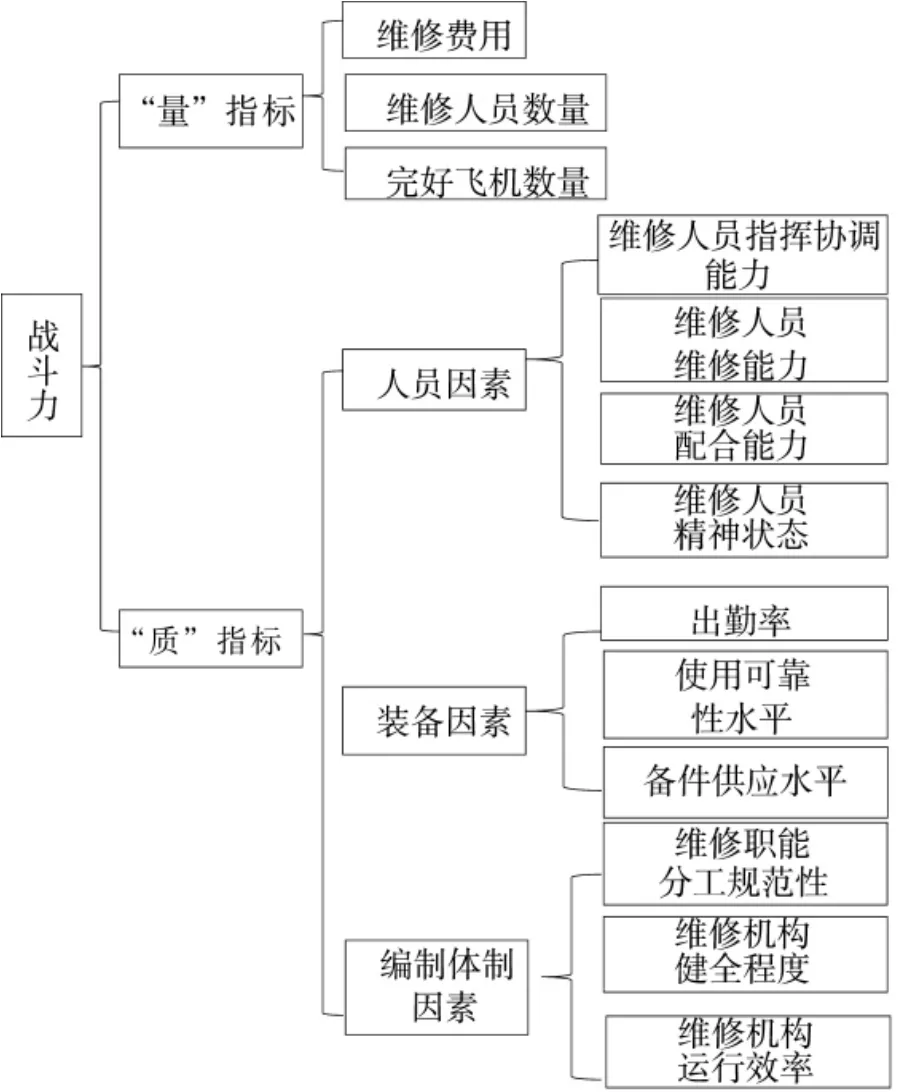
图1 维修费用军事成果评估指标体系
3 维修费用军事成果评估模型
国防经济学家们在分析生产函数与战斗力的相似性基础上,将生产函数概念引入国防经济领域,建立了基于生产函数的军事成果评估模型,用于考察费用支出的军事成果,为量化维修费用军事效益提供了一种可行的方法。
生产函数是描述生产过程中投入的生产要素的某种组合同它可能的最大产出量之间的依存关系的数学表达式。而战斗力评估模型则需要描述在一定的编制体制下,投入的人力、装备和财力所形成的战斗力大小。这一描述与生产函数的描述完全相符,并构造了如下战斗力评估模型[2]。

式中,P为战斗力;R为人力因素;W为装备因素;Z为编制体制因素;N为投入的人的数量;C为投入的维修费用;α、β、γ为R、W、Z 3个因素的权重指数。其中,表示战斗力质的规定,表示战斗力量的规定。
因为战斗力由质和量两方面构成,它的物质载体是装备,装备数量和质量(性能)都会影响战斗力的大小。因此,战斗力量的规定中包括人员、费用投入的同时,还应包括装备的数量因素。显然,这一模型没有考虑装备数量的影响,并不能完整描述战斗力的大小。因此,加入装备数量的影响因素对该战斗力评估模型进行改进,以全面描述战斗力质和量两方面的构成。在这一基础上,可以将战斗力评估模型改进为:

式中,M为完好装备数量,其他参数意义同上。
其中,表示战斗力质的规定,表示战斗力量的规定。它们分别从质和量两方面决定着战斗力的大小。
4 维修费用军事效益评估模型
由维修费用军事效益的定义,维修费用军事效益可用下式表示:
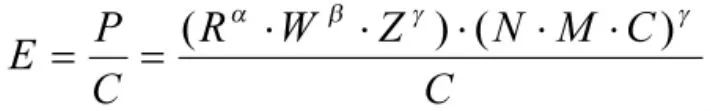
式中,E为维修费用的军事效益;P为战斗力;C为投入的维修费用。
5 维修费用军事效益评估模型各参数的确定
5.1 基于熵权的群组灰色聚类权重指数确定方法
5.1.1 群组灰色聚类分析
假设在某一准则下对n个评价对象进行评价,专家给出的判断矩阵为A,由判断矩阵A归一化求出的评价对象的排序向量为。
其中:
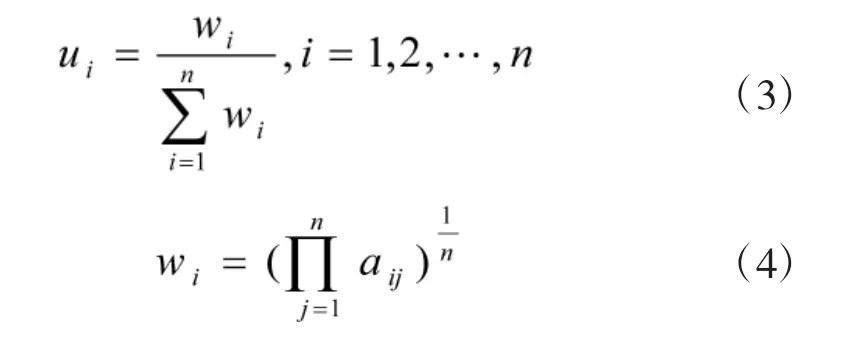
由m个专家的判断矩阵经归一化处理得到的排序向量可以构造出矩阵R:

为了进行灰色关联聚类,需要指标数据具有一致效果测度,即无纲量化和规范化,由排序向量构造出的矩阵R就具有这样的性质,因此,可以看作为标准化矩阵。
对于系统行为序列,,则
的灰色绝对关联度 eij[3]为:

其中,
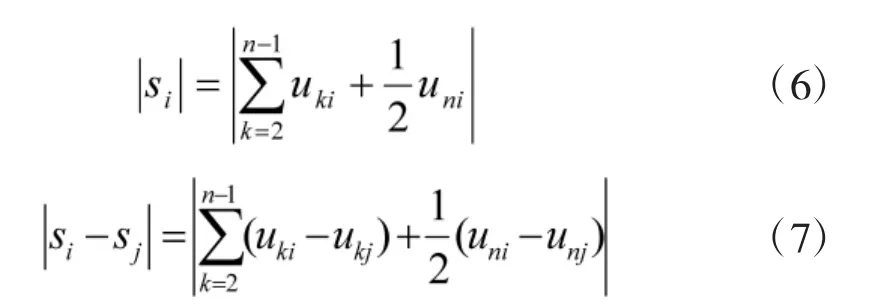
灰色绝对关联度eij具有以下性质[4]:
1);
2) eij只与其 Ui,Uj的几何形状有关,而与其空间位置无关;
3)任何两个序列都不是绝对无关的;
4) Ui与Uj几何上相似程度越大,eij越大。这样就可以得到如下三角矩阵:
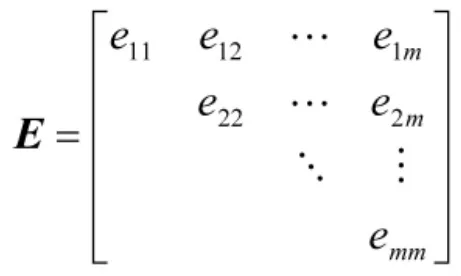
称这个矩阵E为专家群组的灰色关联矩阵。取定阈值,当时,就可以认为Ui与Uj具有同类特性。阈值θ越接近1,分类就越细。
5.1.2 基于熵权的群组赋权分析
群组中专家权重的确定包括两方面:类间权重和类内权重。对于类容量较大的类中个体排序向量所表达的评价信息符合较多专家的意见,对应类应赋予较大的权重系数;对于类容量较小的类中个体排序向量所表达的评价信息有限,只是少部分专家的意见,对应的类应赋予较小的权重系数。
假设m个专家被分为t类,第k位专家所在类中包含个专家,λi为类间权重,αij为第i类中的第j位专家的类内权重,则有:

在信息论中,信息熵是系统无序程度的度量。对于某个特定信源,其信息熵是一个确定的数值[5]。例如某个专家对n个评价指标进行评判,得出的排序向量就可以作为一个离散信源,其概率空间可以表示为:
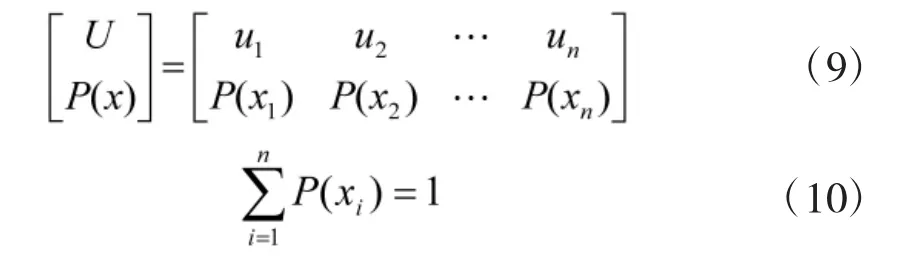
则在一个由m个专家组成的群组中第i个专家的排序向量所蕴含的信息熵可以表示为:

第i个专家的熵权为:

这说明如果专家给出的排序向量的信息熵越小,该专家的逻辑越清晰,信息不确定小,提供的信息量大,在综合评价中所起的作用也越大,应赋予更大的权重,因此,类内权重可以用专家排序向量的信息熵进行度量。
5.1.3 基于熵权的群组灰色聚类权重指数确定步骤
归纳上述推理,可以得到基于熵权的群组灰色聚类决策模型的具体步骤为:
Step1:m个专家对n个评价对象进行两两打分得出的判断矩阵,依据式(3)、式(4)进行归一化得出标准矩阵R。
Step2:根据式(5)~式(7)计算出专家群组的灰色关联矩阵E。
Step3:以为准则,筛选出两两专家聚类的序号集合,其中θ为依据实际聚类需要而确定的阀值。
Step4:对两两聚类集合中的含有相同专家的子集进行“并”操作,确定最终专家聚类结果,并根据式(8)计算类间权重。
Step5:根据式(11)、式(12)计算各个专家排序向量的熵权,即类内专家权重。
Step6:利用线性加权集结群组专家总权重向量W,且。
5.2 因素权值的确定
假设有8位专家,按照AHP层次分析法的评分标准对战斗力评估模型中人力、装备和编制体制3个因素的因素权值α、β、γ进行评价,各位专家列出来的判断矩阵分别为:
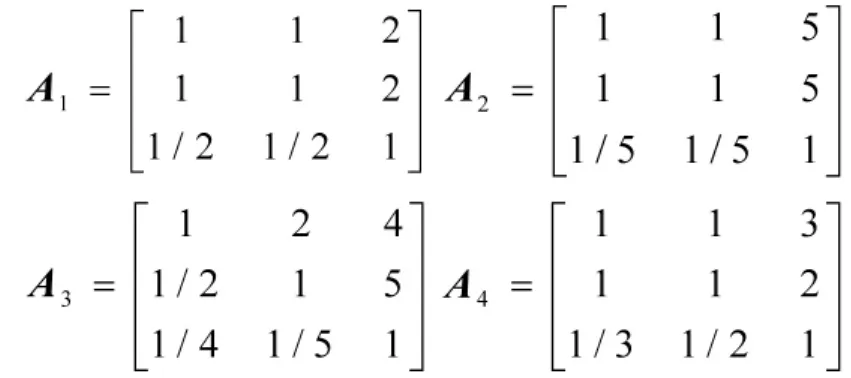
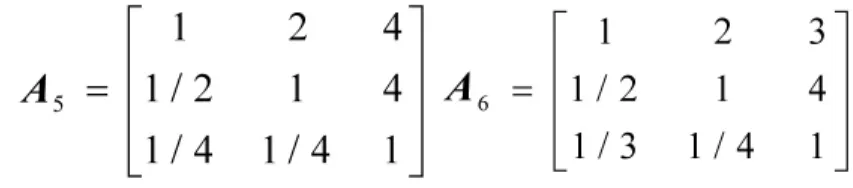
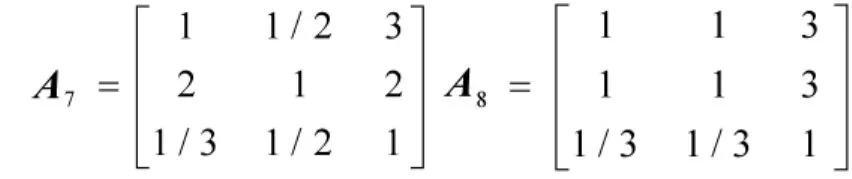
计算各位专家的排序向量构成的标准矩阵R为:

专家群组的灰色关联矩阵E为:

由灰色关联矩阵E可以看出评判方案之间差距可能很小,阈值的选取应尽量接近于1,经试探后发现取阈值θ=0.986时,专家聚类结果比较合理,此时专家的聚类结果是:{(1,2,4,8),(3,5,6),(7)},类间权重为:
问题:矩阵E第1行与第2行相同;类间权重相加,结果不为1。
专家群组的熵向量H为:

根据熵权理论,对于第1类专家,可得其类内权重分别为:α11=0.2370,α12=0.2687,α14=0.2435,α18=0.2504;对于第2类专家,可得其类内权重分别为:α23=0.3389,α25=0.3341,α26=0.3270,对于第 3 类专家,其自成一类,类内权重为:α37=1。
根据以上结果,可以得到群组专家总的权重向量W为:

综合8位专家的总权重和个人排序向量,可得最终的权重向量P为:
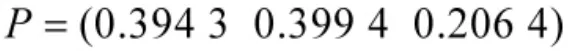
即 α=0.39,β=0.4,γ=0.21。
5.3 装备因素值R的确定
战斗力生成的人力因素本身包含一些影响因子,剔除对战斗力生成影响小且没有规律的因素,论文选定维修人员指挥协调能力、维修人员维修能力、维修人员配合能力和维修人员精神状态作为人力因素的影响因子[6]。

依据基于熵权的群组灰色聚类权重指数确定方法,得到人力因素各影响因子的权重集为:
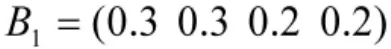
根据人力因素各影响因子的属性特点,设定评语集为:
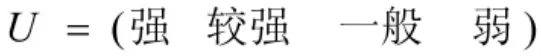
由专家确定评语集对应的加权向量为:
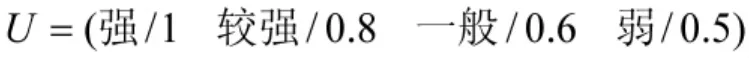
由各位专家对人力因素各影响因子按照其内涵相互比较,分别在4个等级上作出“属于”或“不属于”的二值判断,即当专家判断某影响因子属于某个等级时选定相应的空格,不属于时则空出。如表1所示。
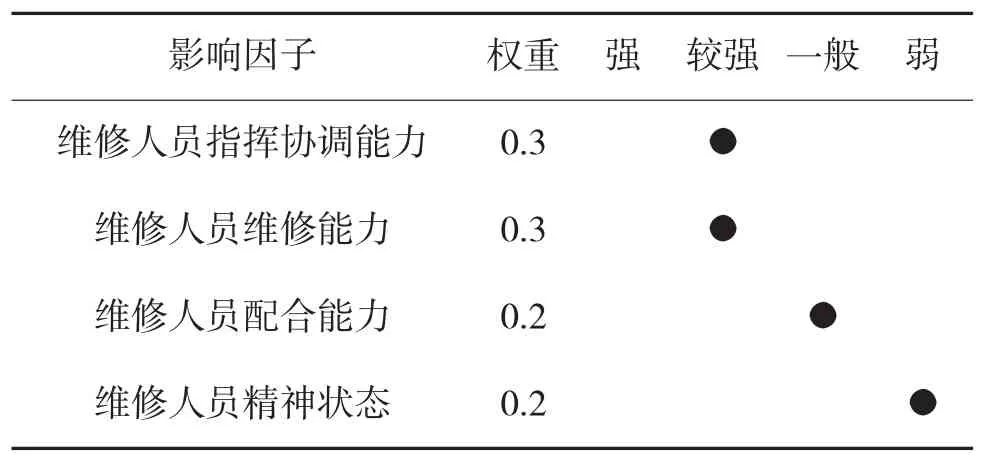
表1 人力因素专家评判表
将各因子得到的相同评语等级的次数进行累加,除以参加评判的专家总数,得到的数值即为该因子反映人力因素的隶属程度。论文取维修人员指挥协调能力的评判集合为:
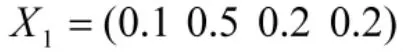
同理,可依次分别确定其他因子的的评判集合。则评判矩阵为:

则人力因素的综合评判结果为:

又评语集的加权向量为:
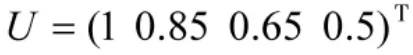
则可得人力因素的综合评判结果为:
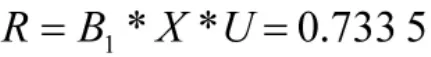
5.4 装备因素值W的确定
同理,选取军用飞机出勤率、使用可靠性水平和备件供应水平为装备因素的影响因子。

依据基于熵权的群组灰色聚类权重指数确定方法,得到装备因素各影响因子的权重集为:

根据装备因素各影响因子的属性特点,设定评语集为:
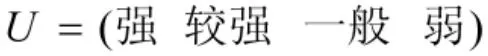
由专家确定评语集对应的加权向量为:
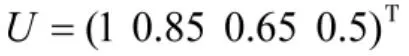
装备因素专家评判表如表2所示。
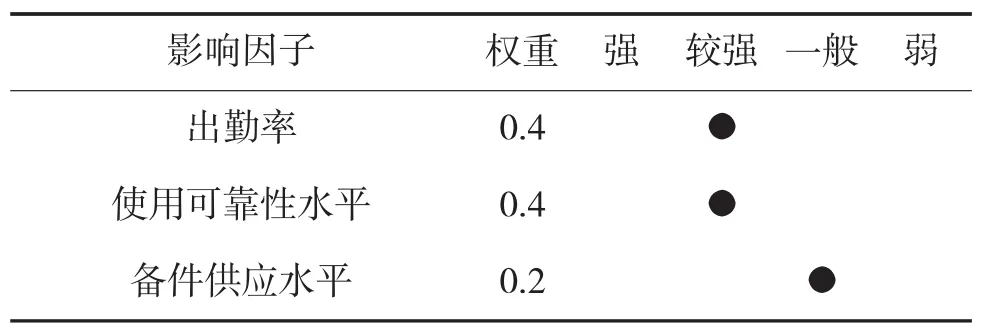
表2 装备因素专家评判表
将各因子得到的相同评语等级的次数进行累加,除以参加评判的专家总数,得到的数值即为该因子反映装备因素的隶属程度。各因子的的评判集合构成的评判矩阵为:

则物力因素的综合评判结果为:
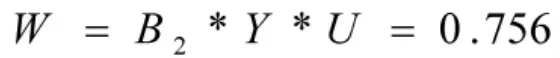
5.5 编制体制因素值Z的确定
选取维修职能分工规范性、维修机构健全程度和维修机构运行效率作为编制体制因素的影响因子。
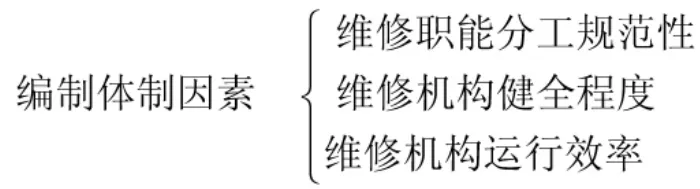
依据基于熵权的群组灰色聚类权重指数确定方法,得到编制体制因素各影响因子的权重集为:

根据编制体制因素各影响因子的属性特点,设定评语集为:
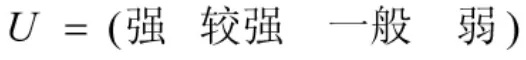
由专家确定评语集对应的加权向量为:
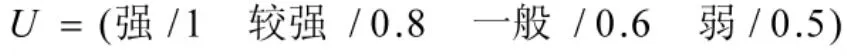
编制体制因素专家评判表如表3所示。
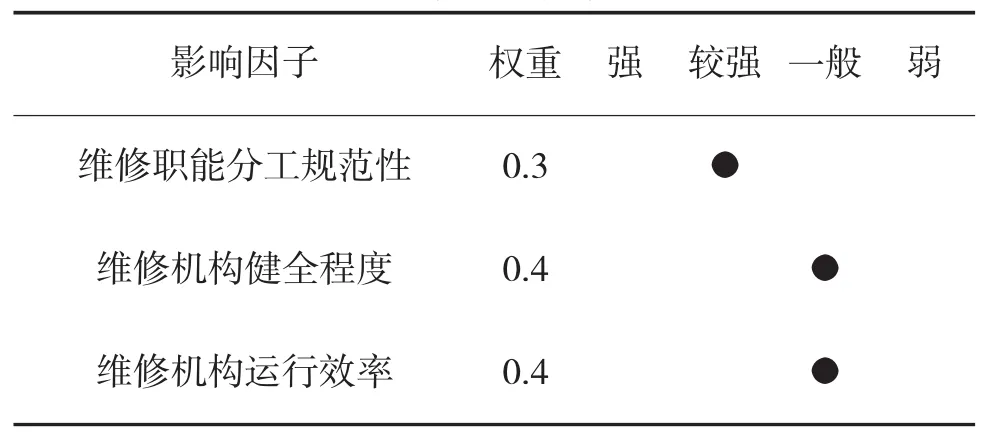
表3 编制体制因素专家评判表
将各因子得到的相同评语等级的次数进行累加,除以参加评判的专家总数,得到的数值即为该因子反映编制体制因素的隶属程度。各因子的评判集合构成的评判矩阵为:

则编制体制因素的综合评判结果为:
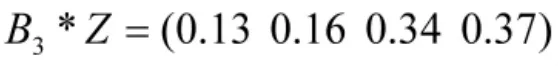
又评语集的加权向量为:
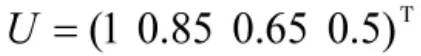
则可得编制体制因素最终的综合评判结果为:
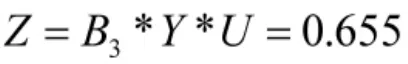
6 维修费用军事效益评估模型各参数的确定
6.1 维修费用军事成果的计算
根据上文确定的评估模型的各因素值,可以计算战斗力的大小。
6.1.1 战斗力的质的大小
由上节确定的评估模型的各因素值可计算战斗力的质的规定的大小为:

6.1.2 战斗力的量的大小
战斗力在量上主要表现为维修人员数量、飞机数量和投入维修费用的额度。这三者不能直接反映战斗力的大小,但可以借助于编制体制的权指数来较为真实地反映这三者对战斗力的影响程度。设共有100架飞机,其编配的维修人员为700人,其中完好数量为83架,维修费用为1000万元,则战斗力的量的规定为:

6.1.3 战斗力大小
求得战斗力质的规定值和量的规定值后,可以给出战斗力大小为:

即在现有编制体制情况下,投入该维修费用产生的军事成果为214.4个战斗力标准当量。
6.2 维修费用军事效益评估
从战斗力的角度来看,在保持编制体制不变的情况下,投入一定的维修费用后,维修人员因素各影响因子的权值都能得到一定提升,装备因素中飞机的性能和备件的供应水平会得到提升,经维修后完好飞机数量会增加。设投入维修费用增加100万元后,飞机完好数增加为88架。此时,对人员因素、装备因素的评判数据进行修正,可得投入一定维修费用之后各因素权值如下。
6.2.1 人力因素R'值的确定
投入一定的维修人员费用后,维修人员指挥协调能力、维修人员维修能力、维修人员配合能力和维修人员精神状态都有提升,人力因素评判集合为:

6.2.2 装备因素W'值的确定
投入维修费用后,飞机的出勤率和备件的供应水平都会提升,装备因素评判集合为:

6.2.3 战斗力的计算
投入维修费用增加100万元后,飞机完好数增加为88架,则战斗力大小为:
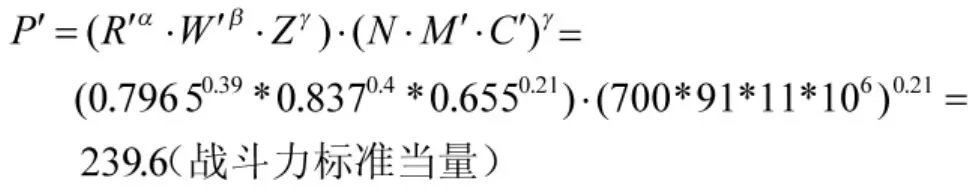
6.2.4 维修费用军事效益
由维修费用军事效益定义,投入一定量的维修费用之后,部队战斗力提高,其增加量为:

维修费用产生的军事效益为:

计算表明,维修后,其军事成果增加了25.2个战斗力标准当量,军事效益为2.52×10-5(战斗力标准当量/元)。
7 结论
对于不同的维修费用投入方案,采用这种方法衡量维修费用的军事效益,可以将装备维修的成果量化,减少不必要的评价环节,从而可以较为科学地评价维修费用军事效益,为确定维修费用的投向、投量提供理论支持。
[1]赵路华.21世纪武器装备技术保障新走向[C]//石家庄:军械工程学院,1997.
[2]欧阳国华,王其华.亚太防务经济论[M].北京:军事科学出版社,1998.
[3]申卯兴,许进,王帅.空中目标威胁排序的灰色聚类决策方法[J].系统工程与电子技术,2008,30(9):1721-1723.
[4]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].5版.北京:科学出版社,2010.
[5]傅祖芸.信息论[M].2版.北京:电子工业出版社,2007.
[6]陈盖凯,杨新广,张红斌,等.基于战备完好率的军用飞机维修费用需求确定方法[J].火力与指挥控制,2016,41(9):32-35.

