基于神经网络的智能车辆导航路径识别模型

陈诚

摘 要： 传统基于PID的车辆导航路径识别模型，基于精准的数学模型实现智能车辆路径控制，在高速情况下具有较低的鲁棒性，智能控制性能差。因此，基于智能车辆运动学模型，设计基于神经网络智能车辆导航路径识别模型结构，通过神经网络对车辆行驶方向进行控制，实现对智能车辆路径导航的控制。将多层前馈型神经网络作为基础结构对T?S模糊系统进行模拟，通过多次训练对神经网络的权值实施调控，完成基于神经网络智能车辆导航路径识别模型的设计。对识别模型实施训练，降低外界的干扰，提高识别模型的控制精度，实现对智能车辆路径导航的控制。实验结果说明，设计的基于神经网络的智能车辆路径导航识别模型控制精度高且鲁棒性较强，智能控制效果佳。

关键词： 神经网络； 智能车辆； 路径导航； 模糊控制； 识别模型； 控制精度； 鲁棒性

中图分类号： TN96?34； TP391.41 文献标识码： A 文章编号： 1004?373X（2018）11?0124?05

Neural network based navigation path recognition model of intelligent vehicle

CHEN Cheng

（Shanghai Jian Qiao University， Shanghai 201306， China）

Abstract： The traditional vehicle navigation path recognition model based on PID， used to realize the intelligent vehicle path control based on precise mathematical model， has low robustness and poor intelligent control performance while driving at a high speed. On the basis of kinematics model of intelligent vehicle， the structure of intelligent vehicle navigation path recognition model based on neural network was designed. The neural network is used to control the driving direction of the vehicle to realize the control of the intelligent vehicle path navigation. The multilayer feed?forward neural network is taken as the basic structure to simulate the T?S fuzzy system. The weight of the neural network is regulated after several trainings to design the neural network based navigation path recognition model of intelligent vehicle. The recognition model is trained to reduce the external interference， improve the control accuracy of the recognition model， and realize the control of the intelligent vehicle path navigation. The experimental results show that the designed intelligent vehicle path navigation recognition model based on neural network has high control accuracy， strong robustness， and perfect intelligent control effect.

Keywords： neural network； intelligent vehicle； path navigation； fuzzy control； recognition model； control accuracy； robustness

0 引 言

当前的智能车辆是智能交通体系发展的关键内容，其在车辆行驶以及军事等领域具有较高的应用价值。智能车辆能够使得交通事故发生概率降低，交通运输效率增加，促进经济效益的提升。智能车辆的导航路径识别是智能车辆控制的关键，可确保车辆自主驾驶的稳定性以及流畅性，具有较高的应用价值[1]。传统基于PID的车辆导航路径识别模型，基于精准的数学模型实现智能车辆路径控制，在高速情况下具有较低的鲁棒性，智能控制性能差。

智能车辆具有较高的动态性以及时延性，受到各种不确定因素的干扰，不能得到精准的数学模型。而基于神经网络的智能控制技术很好地解决了PID方法存在的问题，模糊神经网络无需精准数学模型，基于模糊逻辑则可完成驾驶员的经验控制，并且可通过训练学习产生映射规则，实现车辆的智能控制[2]。本文设计基于神经网络的智能车辆导航路径识别模型，确保智能车辆可高速、精准地跟踪周期期望路径。

1 神经网络的智能车辆导航路径识别模型

1.1 智能车辆运动学模型

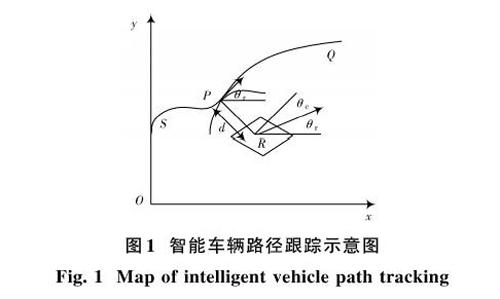
本文通过对智能车辆运动路径进行跟踪，从而为智能车辆导航路径模型的设计提供分析基礎，图1为智能车辆路径跟踪示意图。

将智能车辆的位置坐标表示为[R（x，y，θ）T，][（x，y）]为该智能车辆在世界坐标系下的坐标，[θ]表示智能车辆与[x]轴方向的夹角，[P]点表示智能车辆的位置[R]到车辆运动路线的切点，且[R]点到[P]点的距离用[d]表示，[θr]为车辆运动路线在[P]点处的切向角，[θc]表示方向角的误差角度。因此将智能车辆运动方程表示为：

[x=vcosθy=vsinθθ=ω] （1）

式中：[v]代表智能车辆的瞬时线速度；[ω]表示智能车辆的角速度。

对式（1）进行约束，其约束方程为：

[xsinθ-ycosθ=0] （2）

将智能车辆的位置[R]当作车辆运动路径的参考资料，当前智能车辆的位置坐标为[Rc=（xc，yc，θc）T]，此时的方向角与参考点方向角间的差值为：

[θe=θr-θc] （3）

则此时车辆位置与参考点间的距离为：

[d=（xr-xc）2+（yr-yc）2] （4）

当参考点设置在智能车辆的右侧时，两处距离为正数[D=d]；若参考点在车辆的左侧，距离用负数表示[D=-d]。

1.2 智能车辆路径导航控制模型结构设计

本文基于上述分析的智能车辆动力学模型，基于模糊神经网络设计智能车辆的路径导航控制模型结构，如图2所示。智能车辆的路径偏差信息经过图像处理后得到其横向和方位偏差[3]，再将其经过偏差融合得到综合偏差；采用模糊逻辑控制智能车辆的横向偏差，将得到的综合偏差结果作为控制器的输入数据，前轮转角为输出结果。通过神经网络对车辆行驶方向进行控制[4]，实现对智能车辆路径导航的控制。

1.2.1 基于模糊神经网络智能车辆导航路径识别模型设计

基于模糊神经网络智能车辆导航路径识别模型设计原理：将多层前馈型神经网络作为基础结构对T?S模糊系统进行模拟，进行多次训练对网络的权值进行调试可对网络运行起到优化的作用。模糊技术和神经网络的结合使神经网络具有较强的推理和联想能力[5]。通过模糊C?均值聚类法从车辆数据中心获取模糊聚类中心，将模糊聚类中心作为规则的前件中心，将给定数据分为[n]种不同的类别，[n]种类别的聚类中心用[cj=（c1j，c2j，c3j）， j=1，2，…，n]表示；产生的[n]条模糊规则格式如下：

[If x1 is Al1（x1） and x2 is Al2（x2） then y is yl， l=1，2，…，n] （5）

本文采用高斯函数为T?S模糊神经网络的规则前函数，使函数曲线的平滑性较好，表达式如下：

[μij（xi）=exp-xi-cijbij2，i=1，2；j=1，2，…，n] （6）

式中：[cij]和[bij]分别表示高斯函数的中心和宽度，该中心即为经过模糊C?聚类后的聚类中心。本文将输入变量的分割数设为7，即综合偏差被映射到7个模糊子集，最终得到的基于模糊神经网络结构如图3所示，不同层次间完成不同的任务，将任务的结果传递到下一层次。

第一层是数据输入层，主要接收偏差和偏差变化率，其节点与数据直接相连，可将输入数据进行归一化处理[6]，处理结果被传递到下一层继续处理。第二层是隶属函数生成层，负责将输入的数据进行模糊操作，将数据转化为模糊量，即为模糊子集的隶属度，隶属函数就是经过聚类后的高斯函数。

[μij（xi）=exp-xi-cijbij2] （7）

式中：[μij]表示变量[i]的第[j]个隶属函数；[x]表示控制器的数据输入值；[c]表示函数中心；[b]为函数的宽度；[i]的取值为1或2，用来表示输入变量的维度；[j]表示神经元的数量。

第三、四层均为模糊推理层，共同完成隶属函数的优化和模糊规则的构建[7]。第三层中的神经元为模糊规则前件，输出结果为规则的权重：

[ωl=μAl1（x1）μAl2（x2）] （8）

式中：[Al1]和[Al2]为第一条规则中的模糊集合；[μAl1（x1）]为第一条规则中输入量[x1]属于[μ]集合[Al1]的隶属函数。归一化处理在第四层，每个神经元输出的结果表示对应规则经归一化操作后的比例。

[φl=ωlm=1nωm， l=1，2，…，n] （9）

第五层表示该模糊神经网络的输出层，对输出结果进行控制。输出结果即第四层对应规则归一化操作后比例与神经元权重的乘积，神经元权重表达式为：

[βl=kl?A=pl0+pl1x1+pl2x2] （10）

式中：[kl=pl0 pl1 pl2T]为模糊规则中的参数；[A=1 x1 x2T]；[βl]为模糊规则的后件部分。

假设共使用[n]条控制规则，第五层的输出结果也就是最终的智能车辆导航路径控制结果，为：

[y=l=1nβlφl] （11）

通过模糊C?均值分类和模糊神经网络使模糊神经网络车辆控制器形成49条模糊规则，设第[l]条规则为[Rl]，该规则的表达式为：

[Rl： if x1 is Al1 and x2 is Al2，then ul=pl0+pl1x1+pl2x2， l=1，2，…，49] （12）

式中[ul]表示第[l]条规则的输出结果。

1.2.2 模糊神经网络智能车辆导航路径识别模型训练

從模糊神经网络结构可以看出，智能车辆导航路径识别模型前三层输入层、隐含层和输出层构建出一个前向的网络结构，第四层主要进行神经元的推理[8]。驾驶员驾驶智能车辆来收集道路交通数据，驾驶人员行驶车辆过程中每60 ms收集一次[le]，[U]和[v0]的值，将记录结果汇总成一个数据文件。该数据收集时间共20 min，驾驶员驾驶智能车辆的导航路径包括直线?曲线?直线或S曲线?直线?S曲线等4条路径。将收集到异常的数据进行剔除[9]，得到基于神经网络的智能车辆导航路径识别模型的样本，经驾驶员多次驾驶，得到路径S曲线?直线?S曲线的600组数据，控制器初始学习率为0.3，动量系数为0.9，误差概率为0.1%，经过多次训练得到其隐层的权值[W1]和阈值[B1，]输出层权值[W2]和阈值[B2。]采用T?S模式设计模糊神经网络的智能车辆导航路径识别模型的学习效率为5%，将训练样本数据导入神经网络结构中进行离线训练，训练结束后训练样本具有记忆功能，离线训练能对训练样本进行模糊参数的调整[10]，使模糊的神经网络高效地模拟输入与输出的关系，降低外界的干扰，提高智能车辆导航路径识别模型的控制精度。

2 实验结果与分析

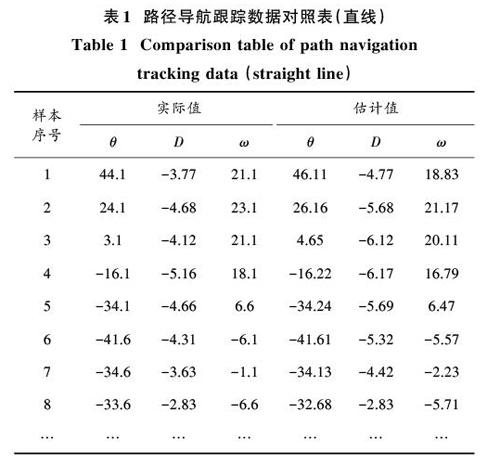
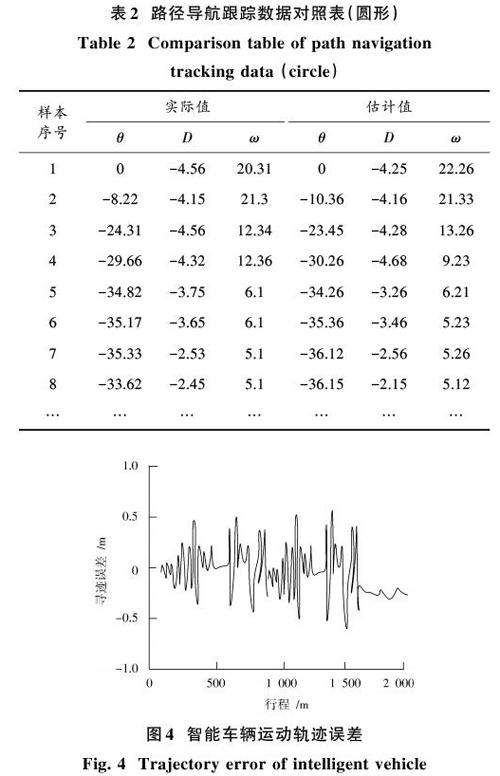
实验采用本文设计的基于神经网络的智能车辆导航路径识别模型，对某类型智能车辆实施控制。该识别模型以1 m/s的速度分别对智能车辆进行直线路径和圆形路径导航，实施Matlab仿真，原始样本数据通过驾驶智能车辆获取。假设实验跟踪的数据在20个样本内均能采集到精确的数据，直线上运动角速度为0 （°）/s，圆形上运动角速度为12.264 （°）/s。对20个样本进行实验仿真，训练1 000次。表1和表2分别为本文识别模型对实验智能车辆直线和圆形的路径导航跟踪数据。

表1和表2中，[θ]表示方向角误差，[D]表示距离误差，[ω]表示角速度误差。从表1和表2对直线和圆形路径导航跟踪结果可以看出，经过本文模型的模糊神经网络训练后，车辆角速度变得更平稳，收敛度更高且鲁棒性强。

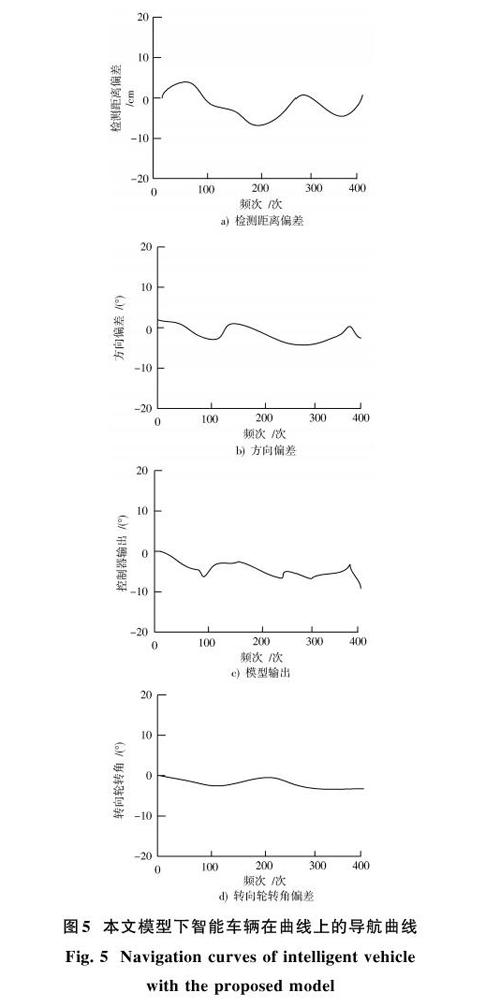
图4为采用本文识别模型控制后智能车辆路径导航中的运动轨迹误差，从图4中可以看出，运动轨迹的误差在0.5 m之内，表明本文模型的精度较高，能够实现智能车辆路径导航的准确识别。从图中还能看出波动较高的峰值都处在道路曲率较高且相对波动率较高的位置，同实际的驾驶经验一致。

为了对本文识别模型的工作效果进行测试，设计基于本文识别模型的智能车辆路径导航实验，智能车辆的行驶路径有直线、曲线和S型三种。曲线路径要求偏向角在15°以内，图5为基于本文识别模型控制下的智能车辆在曲线上的导航曲线，实验环境为普通的柏油马路，采用IPC?6809工控机，内存为256 MB，CCD使用德国生产的BASLERA602fc，智能车辆的启动速度为10 km/h，最大限速为20 km/h。从图5中可以看出，车辆运动路线为曲线时其侧向偏差和方向偏差为负相关，其偏差范围在10 cm之内，符合智能车辆导航控制器的要求，说明本文识别模型工作效果优，可对智能车辆进行高质量导航控制。

3 结 论

本文设计基于神经网络的智能车辆导航路径识别模型，通过模糊神经网络实现智能车辆路径的经验控制，对识别模型实施训练提高了模型的控制精度，实现智能车辆路径的高精度控制。

参考文献

[1] 倪捷，刘志强.基于驾驶人决策机制的换道意图识别模型[J].交通运输系统工程与信息，2016，16（1）：58?63.

NI Jie， LIU Zhiqiang. The model of lane change based on driver decision?making mechanism [J]. Transportation system enginee?ring and information， 2016， 16（1）： 58?63.

[2] 周青，邹凡.基于神经网络的产业技术创新战略联盟冲突识别模型[J].技术经济，2016，35（4）：44?51.

ZHOU Qing， ZOU Fan. Conflict identification model of industrial technology innovation strategy alliance based on neural network [J]. Technology economy， 2016， 35（4）： 44?51.

[3] 刘占文，赵祥模，李强，等.基于图模型与卷积神经网络的交通标志识别方法[J].交通运输工程学报，2016，16（5）：122?131.

LIU Zhanwen， ZHAO Xiangmo， LI Qiang， et al. Method of identification of traffic signs based on graph model and convolution neural network [J]. Journal of transport engineering， 2016， 16（5）： 122?131.

[4] 要会娟，浮洁，张丽香.基于神经网络的磁流变阻尼器逆向模型辨识研究[J].计算机仿真，2015，32（12）：408?412.

YAO Huijuan， FU Jie， ZHANG Lixiang. Research on the reverse model identification of magnetorheological dampers based on neural network [J]. Computer simulation， 2015， 32（12）： 408?412.

[5] 邓召学，郑玲，郭敏敏，等.基于遗传BP神经网络的磁流变悬置模型辨识[J].电子科技大学学报，2014，43（6）：955?960.

DENG Zhaoxue， ZHENG Ling， GUO Minmin， et al. Identification of magnetorheological suspension model based on genetic BP neural network [J]. Journal of University of Electronic Science and Technology of China， 2014， 43（6）： 955?960.

[6] 孟祥海，覃薇，邓晓庆.基于神经网络的山岭重丘区高速公路事故预测模型[J].公路交通科技，2016，33（3）：102?108.

MENG Xianghai， QIN Wei， DENG Xiaoqing. Highway accident prediction model in mountain ridge area based on neural network [J]. Highway traffic technology， 2016， 33（3）： 102?108.

[7] 林文如，陳腾林，林国福.基于改进神经网络的非满载车辆路线优化模型[J].计算机工程与应用，2015，51（16）：239?242.

LIN Wenru， CHEN Tenglin， LIN Guofu. Vehicle route optimization model based on improvement neural network [J]. Computer engineering and applications， 2015， 51（16）： 239?242.

[8] 诸云，高宁波，郑丽媛.基于神经网络的经济圈道路交通安全综合测度模型[J].中国安全科学学报，2015，25（10）：22?28.

ZHU Yun， GAO Ningbo， ZHENG Liyuan. A comprehensive measurement model of road traffic safety based on neural networks [J]. China journal of security science， 2015， 25（10）： 22?28.

[9] 蒋士正，许榕，陈启美.基于变量选择?神经网络模型的复杂路网短时交通流预测[J].上海交通大学学报，2015，49（2）：281?286.

JIANG Shizheng， XU Rong， CHEN Qimei. Short?term traffic flow prediction for complex road network based on variable selection neural network [J]. Journal of Shanghai Jiao Tong University， 2015， 49（2）： 281?286.

[10] 张萌，娄胜利，丁亮.基于反向传播神经网络的驾驶人人际与情绪危险性模型[J].公路交通科技，2015，32（1）：140?144.

ZHANG Meng， LOU Shengli， DING Liang. The driver′s interpersonal and emotional risk model based on back?propagation neural network [J]. Highway traffic technology， 2015， 32（1）： 140?144.