基于碳纳米管薄膜电学成像的复合材料结构损伤识别研究*

杨周杰,严 刚

(南京航空航天大学航空宇航学院,机械结构力学及控制国家重点实验室,南京 210016)

复合材料因其比强度高、比刚度大、材料性能可设计等一系列优点,被越来越广泛地应用在航空航天等领域。但复合材料结构在使用过程中,不可避免地会受到损伤,严重削弱结构的强度和稳定性。如果这些损伤不能够被及时发现而任其发展,将可能导致灾难性的后果,因此对复合材料结构的完整性进行持续的监测和准确的评估已经越来越迫切。

随着纳米科技的迅速发展,近年来基于碳纳米材料的结构健康监测技术得到了极大的关注[1]。碳纳米管所具有的优异力学性能和导电能力,以及容易与结构集成的特点,使其成为理想的自感应传感材料[2]。如Thostenson和Chou将碳纳米管分散在复合材料树脂基体中作为分布式传感器,通过基体的电阻变化评估复合材料变形产生的损伤[3];Mactabi等人利用碳纳米管改性的树脂作为粘结剂对胶接结构进行监测,通过粘结层电阻变化来判定疲劳加载过程中产生的损伤[4]。这些研究大都针对复合材料一维结构,并且只能定性地监测到损伤的产生和发展。为了丰富所监测损伤的信息,很多研究者针对复合材料二维板壳结构,提出了采用传感网络的测试方法。如Proper等人在碳纳米管改性的凯夫拉复合材料板表面布置电极网络,建立了网格点电压变化与冲击损伤位置之间的对应关系[5];Naghashpour等人在碳纳米复合材料板表面布置等间隔分布的电极网络,通过相邻电极之间电阻的变化来判断这两个电极中间或附近是否存在损伤[6]。这些方法大多能较好地获取损伤位置信息,但需要布置大量的电极对整个结构进行覆盖,识别的精度取决于电极的密度。

为提高损伤识别的准确性,一种在医学领域发展起来的电学成像技术被用于对碳纳米复合材料结构中的损伤进行定量成像识别[7-8]。电学成像是一种软场层析成像方法,通过一组置于物体表面的电极,在微小电流激励的同时测量物体表面的边界电压,结合重建算法来反演物体的内部电特性(通常是电导率或电阻率)分布[9-11]。如Baltopoulos等人利用玻璃纤维复合材料树脂基体中的碳纳米管网络进行损伤评估,结合Tikhonov正则化成像算法,实现了对孔洞和裂纹损伤的识别[12];Gallo等人研究了碳纳米管改性玻璃纤维板结构中孔洞、冲击损伤等损伤形式,采用类似的正则化算法进行电阻抗成像,同时利用质心法确定了损伤中心位置[13]。这些研究都表明了电学成像与碳纳米技术结合对结构进行健康监测的良好应用前景,但还存在一些问题,一是碳纳米管所具有的团聚现象使其难以均匀地分散到复合材料树脂基体中,形成的导电网络在各个方向很不均匀,导电能力下降,影响了电学成像技术的实施;二是目前采用的成像算法主要是基于L2范数的Tikhonov正则化算法,容易导致解过度平滑,重建图像边缘较为模糊,影响损伤识别效果。

基于以上分析,本文提出一种应用导电能力更强更均匀的碳纳米管薄膜作为智能感知层,结合电学成像对复合材料结构进行损伤识别的新方法。为了更好的重建电导率变化分布图像,结合L曲线法选择最优的正则化参数,采用基于L1范数正则化的最小二乘法进行图像重建。进行了实验研究,并与常用的Tikhonov正则化方法比较,验证本文所提出方法的有效性。

1 电学成像重建算法

1.1 正向建模

电学成像为恒定电流场模型,场域内没有电流源。根据Maxwell方程和似稳场假设,场域内的电势分布函数u满足

·(σu)=0

(1)

式中:σ为电导率。

对于采用电流激励方式的电学成像系统,符合Neumann边界条件,即第2类边界条件:

(2)

(3)

(4)

式中:zl为电极与场域内介质的接触电阻,Ul为电极l上的测量电压值,Il为电极l上的激励电流,el为第l个电极,n为边界S的单位法向矢量,Ω为测量区域。

电学成像正问题是求解场域内电场的分布,获得场域的边界电压值与电导率分布的对应关系,即灵敏度矩阵。对于一般形状的场域模型,由于推导过程复杂,很难通过解析法进行正问题的求解,通常情况下,选用有限元法(FEM)进行求解。对于该灵敏度矩阵J,可以结合Geselowitz灵敏度定理计算得到[14]

(5)

式中:ui为第i个激励电极对作用下的电势,uj为单位电流激励作用下的第j个测量电极对的电势。

1.2 反向重建算法

电学成像反问题是根据测量得到的边界电压数据,结合场域电学性质的正向模型,反演得到内部的电导率分布。通常采用最小二乘法来优化电压测量值与理论值的差值,即

(6)

式中:Vm为实验测得的边界电压值,F(σ)为结合场域的电导率分布σ利用有限元法计算得到的边界电压值。

当场域的初始电导率分布σ0已知时,可以利用Taylor级数将F(σ)展开,将式(6)转化为线性反问题,获得电导率变化的分布,即

(7)

式中:ΔV为边界电压变化值,Δσ为电导率变化值。

但式(7)表示的反问题通常是病态和不适定的,为获得有界的稳定解,一般采用Tikhonov正则化方法将该图像重建问题转化为[15]:

(8)

式中:μ为正则化参数,I为单位矩阵。

然而对复合材料结构进行损伤识别时,被测区域的介质往往存在不连续性,为了反映问题的稀疏性和改善图像重建质量,重新定义误差估计方式,用L1范数表示罚函数,采用基于L1范数正则化的最小二乘法进行图像重建。L1范数正则化的目标函数为[16]:

(9)

式中:‖Δσ‖1=Σi|Δσi|为Δσ的L1范数,λ为正则化参数。

由于L1范数正则化最小平方规划问题是不可微的凸函数,无法确定其解析解。引进变量vi(vi≥0),将式(9)转换为如下的凸二次问题

(10)

采用内点法对该问题进行求解,该方法是由压缩传感理论发展起来的,适用于大型稀疏线性方程组求解[16]。为模拟不等式的限制,对约束条件-vi≤Δσi≤vi定义对数门限函数Φ(Δσ,v),将式(10)转化为无约束二次规划问题,给出凸函数

(11)

式中:参数t的取值范围为t>0,对数门限函数Φ(Δσ,v)=-Σilg(vi+Δσi)-Σilg(vi-Δσ)。

采用Newton迭代法为基本原理,每次迭代令t增大,序列t典型的增长方式为t=t0,βt0,β2t0…,其中β>1。搜索方向可通过Newton系统精确求解得到[17],即

(12)

式中:H=2φt(Δσ,v)为Hessian矩阵。

正则化参数λ的选取是求解问题的关键,决定着计算速度和成像质量。通常正则化参数的选取方法分为先验选取法和后验选取法,先验选取法便于进行理论分析,但对于损伤重建算法,在实际求解过程中很难预先给出关于解的任何先验信息,因而计算中更多的是利用后验选取法。对于式(9),参数λ的取值范围是0<λ<‖2JTΔV‖∞(‖·‖∞表示向量的无穷范数)[16]。当λ取值过小,残差项较小,计算结果接近问题的真实解,但必然会影响计算效率和解的稳定性;当λ取值过大时,正则化误差占主导地位,计算结果会偏离真实解,严重影响解的准确性,因此需要在残差项和正则化项之间寻求一种数量平衡关系。从本质上讲,参数λ取决于问题的稀疏程度,在此采用L曲线法来确定最优的参数λ。对于式(9),定义关于λ的参数方程[18]

(13)

在log-log对数坐标尺度下,经过曲线拟合会得到一条近似“L”形状的曲线,选取这条曲线的最大拐点作为最优的参数λ。

2 实验研究

2.1 测试对象与装置

实验研究中,选用一种尺寸为100 mm×100 mm,厚度约为6 μm～10 μm,采用化学气相沉积法制备的碳纳米管薄膜(JCNTF-20C,南京吉仓纳米科技有限公司)作为智能感知层,对一块厚度为2 mm的玻璃纤维复合材料(GFRP)层合板进行损伤识别。将碳纳米管薄膜用环氧树脂粘贴在层合板表面,层合板产生损伤时将引起薄膜对应位置发生电导率变化,从而可以利用此电导率变化进行损伤识别。如图1所示,采用导电银漆(SCP03B,英特沃斯(北京)科技有限公司)在薄膜的四周边缘等间距布置20个电极,并使用导电银胶(SINWE3703,深圳市鑫威新材料股份有限公司)将细导线与电极相连。

图1 粘有碳纳米管薄膜感应层的GFRP层合板

为了保证测量精度和测量效率,搭建了一套电学成像实验测试系统,如图2所示。该系统主要包括精密电源(KEITHLEY 6221)、纳伏表(KEITHLEY 2182A)、矩阵开关(KEITHLEY 3706A-S)、端子模块(KEITHLEY 3723-ST)及控制器(Lenovo工作站 P510)。使用基于LabVIEW开发的系统软件根据一定的测量协议进行电极间的切换,并在对指定电极对进行电流激励的同时实现对其他电极间电压的自动测量。

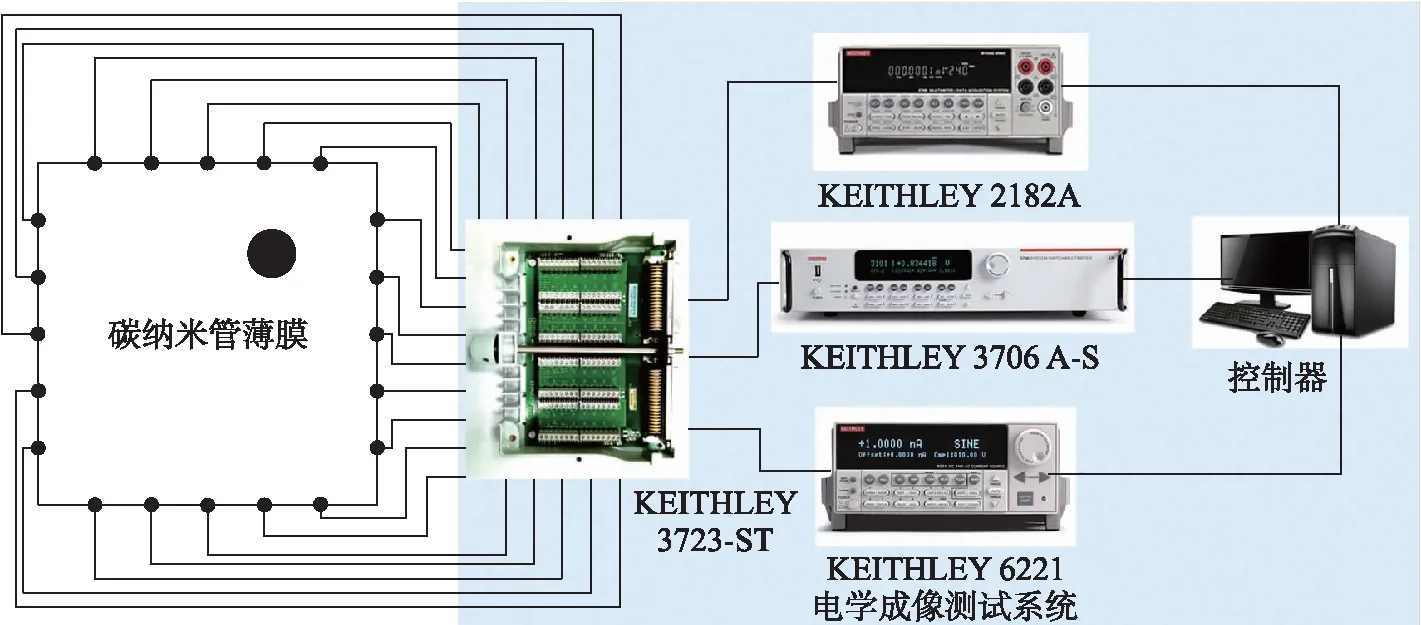
图2 电学成像实验测试系统

2.2 测试过程

该实验测试中,选用相邻电极模式进行实验测量,如图3所示,共有20组相邻电极对,当电流激励一组电极对时,依次测量与电流激励无关的余下的17组电极对间的电压值。本实验采用的激励电流大小均为100 mA,由于需要依次激励每一组电极对,共激励20次,最终共测得17×20=340个边界电压值。根据电学成像重建原理,本实验需要测量两组电压值(损伤发生前后),首先,在薄膜完整时测量一组电压值作为均匀状态下的参考值;随后,薄膜受到破坏,利用相同的测试原理再次进行测量,得到损伤状态下的一组电压值;最终,利用电学成像算法对这两组电压值进行电导率变化重建,并以图像形式显示以识别损伤信息。

图3 电学成像测试原理及过程

图4 试验件一孔损伤位置

3 实验结果

本实验通过钻孔来模拟GFRP层合板的损伤形式,钻孔会导致对应位置薄膜的破坏,从而引起该区域电场的扰动。如图4所示,在试验件上钻取一个12 mm的通孔,通过电学成像测试系统测得试验件损伤前后的两组边界电压值。基于电学成像重建算法,通过MATLAB(R2014b,MathWorks®)对数据进行处理,重建获得电导率变化图像。

为了验证L1范数正则化的优点,将其与常用的Tikhonov正则化进行对比分析。根据边界电压值的变化及该场域的灵敏度矩阵J,利用L曲线法分别为L1范数正则化和Tikhonov正则化选取适当的正则化参数,如图5所示,选取的正则化参数分别为λ=8.160 9×10-4和μ=1.66×10-2。

如图6(a)所示,重建电导率变化分布的有限元模型包含3 200个单元。结合选取的正则化参数,分别用L1范数正则化和Tikhonov正则化进行图像重建,图6(b)和6(c)显示出两种算法的重建效果。不难看出,两种算法均可有效地显示出损伤区域,但L1范数正则化重建图像的伪影较少,而Tikhonov正则化重建的图像较为模糊。

图中圆圈表示损伤实际位置及尺寸

图5 结合L曲线法确定最优正则化参数

为了进一步比较两种重建算法对边缘信息的保护效果,绘制出重建结果中沿截面的电导率变化量分布图。通常认为分布图的半峰全宽(FWHM)越小,则对应的重建效果更为理想[19]。如图7所示,L1范数正则化获得的分布图的半峰全宽明显窄于Tikhonov正则化,更接近损伤实际尺寸,且分布图两端电极附近的干扰更少。

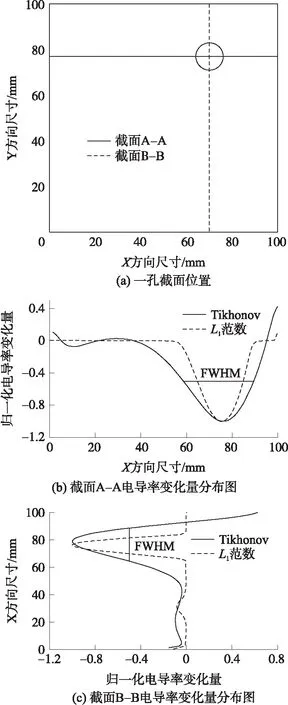
图7 沿截面的电导率变化量分布图

此外,利用相同的原理及方法,对两孔损伤形式进行图像重建。如图8所示,当对试验件钻取两个通孔时,依旧能够获得较理想的重建图像,与Tikhonov正则化相比,L1范数正则化重建图像中的干扰信息明显较少,显示出的损伤区域更接近真实情况。

同样地,为了进行更直观的分析,如图9所示,绘制出沿截面方向的电导率变化量分布图。L1范数正则化获得的分布图的半峰全宽更窄,损伤边界信息更好。但结合图8来看,左下孔的实际成像效果略差于右上孔,造成该现象的可能原因有电极实际分布位置及尺寸的误差、钻孔对孔洞周围薄膜的破坏程度不同、薄膜的电导率存在均匀性问题等。

图中黄色圆圈表示损伤实际位置及尺寸

图9 沿截面的电导率变化量分布图

4 结论

本文通过实验研究,分析和验证了利用碳纳米管薄膜作为智能感应层,结合电学成像算法对复合材料进行结构健康监测的可行性和有效性。实验结果表明,碳纳米管薄膜所具有的良好导电性使其在作为智能传感层时,能够通过其电导率的变化感应到复合材料结构中损伤的存在;而采用基于L1范数正则化的最小二乘法进行电导率变化图像重建,改善了传统的L2范数正则化算法导致重建图像过于平滑的缺点,能够有效地显示出复合材料结构中损伤的情况,帮助提高损伤识别的精度。

参考文献:

[1] 朱永凯,陈盛票,田贵云,等. 基于碳纳米管压阻效应的复合材料结构健康监测技术[J]. 无损检测,2010,32(9):664-669.

[2] Arronche L,Saponara V L,Yesil S,et al. Impact Damage Sensing of Multiscale Composites through Epoxy Matrix Containing Carbon Nanotubes[J]. Journal of Applied Polymer Science,2013,128(5):2797-2806.

[3] Thostenson E,Chou T W. Carbon Nanotube Networks:Sensing of Distributed Strain and Damage for Life Prediction and Self Healing[J]. Advanced Materials,2010,18(21):2837-2841.

[4] Mactabi R,Rosca I D,Hoa S V. Monitoring the Integrity of Adhesive Joints during Fatigue Loading Using Carbon Nanotubes[J]. Composites Science and Technology,2013,78(2):1-9.

[5] Proper A,Zhang W,Bartolucci S,et al. In-Situ Detection of Impact Damage in Composites Using Carbon Nanotube Sensor Networks[J]. Nanoscience and Nanotechnology Letters,2009,1(1):3-7.

[6] Naghashpour A,Van H S. A Technique for Real-Time Detection,Location and Quantification of Damage in Large Polymer Composite Structures Made of Electrically Non-Conductive Fibers and Carbon Nanotube Networks[J]. Nanotechnology,2013,24(45):455502.

[7] Harikumar R,Prabu R,Raghavan S. Electrical Impedance Tomography(EIT)and Its Medical Applications:A Review[J]. International Journal of Soft Computing and Engineering,2013,3(4):193-198.

[8] Hallaji M,Pour-Ghaz M. A New Sensing Skin for Qualitative Damage Detection in Concrete Elements:Rapid Difference Imaging with Electrical Resistance Tomography[J]. NDT&E International,2014,68(68):13-21.

[9] Djajaputra D. Electrical Impedance Tomography:Methods,History and Applications[J]. Medical Physics,2005,32(8):2731-2731.

[10] 黄华芳,杨涛,陈晓艳,等. 基于同步测量的电阻抗层析成像系统研究[J]. 传感技术学报,2015,28(10):1575-1580.

[11] 汪剑鸣,李文聪,张荣华,等. 基于最大期望算法的电阻抗成像系统的图像重建[J]. 传感技术学报,2015(11):1652-1658.

[12] Baltopoulos A,Polydorides N,Pambaguian L,et al. Exploiting Carbon Nanotube Networks for Damage Assessment of Fiber Reinforced Composites[J]. Composites Part B,2015,76:149-158.

[13] Gallo G J,Thostenson E T. Spatial Damage Detection in Electrically Anisotropic Fiber-Reinforced Composites Using Carbon Nanotube networks[J]. Composite Structures,2016,141:14-23.

[14] Vauhkonen M. Electrical Impedance Tomography and Prior Information[D]. Finland:University of Kuopio,1997.

[15] 刘继军. 不适定问题的正则化方法及应用[M]. 北京:科学出版社,2005:46-54.

[16] Kim S J,Koh K,Lustig M,et al. An Interior-Point Method for Large-Scale 1-Regularized Least Squares[J]. IEEE Journal of Selected Topics in Signal Processing,2007,1(4):606-617.

[17] 张玲玲,王化祥,范文茹. 基于1范数的电阻层析成像图像重建算法[J]. 天津大学学报(自然科学与工程技术版),2011,44(9):786-790.

[18] Hansen,Christian P. Analysis of Discrete Ill-Posed Problems by Means of theL-Curve[J]. Siam Review,1992,34(4):561-580.

[19] 王兵元,陈玮婷,马文娟,等. 基于非负约束L1-范数正则化的乳腺扩散光学层析成像重建方法[J]. 光学学报,2016,36(11):204-210.