新颖高温超导紧凑型双CT结构带通滤波器
周立国,李怀明,褚慧敏,杨常林,谭雪薇,粟立勇,羊 恺
( 1. 电子科技大学航空航天学院 成都 611731;2. 中国电子科技集团公司第五十五研究所 南京 210001)
高温超导薄膜在液氮温度下工作时具有极低的微波表面电阻,其在微波领域的应用研究越来越多,极大地推动了通信技术、雷达技术和电子对抗技术的发展。高温超导微波滤波器及滤波器组是高温超导微波应用的关键器件之一,比传统波导器件具有更好的高选择性、更低的插损等特性,并兼具平面电路体积小、重量轻、易于与其他微波固态电路进行混合集成的优点,备受移动通讯和卫星通讯的青睐。国内和国际在这方面的研究工作已卓有成效,出现了多种超导滤波器的设计方法和手段,鉴于加工成本及工艺等方面的问题[1-3],科研工作者特别在滤波器小型化和高选择性方面做了许多研究工作,设计了多种新颖的结构[4-5]。本文设计了一种全新的平面单螺旋菱形谐振器结构,用该结构设计的滤波器结构上更为紧凑、电路整体更加美观,该谐振器结构易于实现CT单元。平面单螺旋菱形谐振器设计的CT单元在设计滤波器时能够产生一个传输零点,相对于无传输零点的滤波器,该结构能明显地提高滤波器的带外抑制度[6-8]。该结构的高温超导带通滤波器不但具有插损小、边带陡峭、体积小、阻带宽的特点,而且视觉上具有立体感的美观效果。该新颖结构的高温超导带通滤波器可广泛应用于移动通讯和卫星通讯领域[1,7-11]。
1 平面单螺旋菱形谐振器的设计
图1a为经典的平面单螺旋谐振器的基本结构,前期的科研人员已对其优势做了详细的说明[6-11]。本文在经典的平面单螺旋谐振器的基本结构的基础上,设计一种新型的平面单螺旋菱形谐振器结构,可方便地搭建紧凑型CT单元以实现整个滤波器的小型化。将半波长、0.1 mm线宽的经典平面单螺旋谐振器的一边向上或下拉伸30°,获得全新结构的平面单螺旋线菱形谐振器,如图1b所示,该菱形谐振器结构采用倾斜线方式来完成半波长谐振器的螺旋。平面单螺旋菱形谐振结构简单,方便利用电磁全波分析软件进行辅助设计与调试优化。菱形的30o特殊性可以方便搭建出结构紧凑的CT单元(如图5所示),避免了使用交叉耦合线来实现CT单元。与采用交叉耦合线设计CT单元的滤波器相比,该方法设计的滤波器在加工方面降低了对光刻工艺的要求,可以提高成品率。通过采用IE3D软件进行电磁仿真,该谐振器的结构参数如图1所示。图1中经典平面单螺旋线谐振器和平面单螺旋线菱形谐振器的寄生谐振频率都在二倍频以外,频率响应如图2所示。由图2知,在基波谐振频率响应相同时,平面单螺旋线菱形谐振器的寄生谐振频率更具有优势。

图1 两种平面单螺旋谐振器结构

图2 平面单螺旋线谐振器频率响应曲线
2 CT结构滤波器的设计理论
图3所示为典型的CT滤波器的拓扑结构,带数字的小菱形代表一个谐振器,两菱形之间的实线代表直接耦合,虚线代表交叉耦合。当信号由滤波器的输入端到达输出端时,在6个谐振器组成的分布式结构中就有不同的路径可以通过,如图3中可以形成: ① →②→③→④→⑤→⑥、①→③→④→⑤→⑥、①→ ② → ③ → ④ → ⑥、① → ③ → ④ → ⑥4条路径。通过调整谐振器之间的耦合形式,对信号通过不同通路的相位进行控制。若能使得信号相位叠加,就可以引入传输零点;若能使得相位补偿,则能改善滤波器群时延特性。CT单元由3个谐振器组成,它们之间通过直接耦合和交叉耦合实现。文献[1,5]对谐振器和交叉耦合的电容性、电磁性耦合理论进行了阐述。结合谐振器工作频带的高频端、低频端相位差变化,分析了信号通过滤波器后相位的变化和引入传输零点的原理。

图3 典型的CT滤波器的拓扑结构

图4 CT单元的等效电路模型
按照微带滤波器的综合设计方式可以得到如图4所示的CT单元的等效电路模型,其中M12和M23为直接耦合系数,M13为交叉耦合系数,Qe1和Qe2为滤波器的输入输出外部品质因数,L1、L2、L3和C1、C2、C3分别为谐振器的等效电感、电容。
经典滤波器设计理论中,外部品质因数eQ为:

式中,90ω±Δ为偏离中心频率± 90°处的两频点的频率差值。
滤波器中两谐振器之间的耦合系数:

式中,f1和f2为两个谐振器的谐振频率。
对于微带线滤波器,图4中LC为半波长谐振器的等效,传输线波长:

式中,c为光速;f为频率;rε为有效介电常数。
3 紧凑型CT单元的设计
采用前文设计的平面单螺旋线菱形谐振器,将图1b中的谐振器作为图5中的CT单元的谐振器1,然后通过对谐振器1在0°方向镜像获得谐振器3,对谐振器3再逆时针旋转120°获得谐振器2。最终通过旋转3个谐振器设计出一个完整的CT单元结构,如图5所示。谐振器1及谐振器3可以方便与前后级实现磁场耦合。通常当两谐振器之间距离增大时谐振器之间的耦合变弱,反之耦合变强,所以通过调整各个谐振器之间的相互距离可以获得不同的频率响应[5,12]。该CT结构存在3个距离变量d12、d23、d13,所以耦合强度的调整更加灵活。例如,当图5的CT结构中d13=0.35 mm时,随着d12=0.28 mm、d23=0.17 mm逐渐增大到d12=0.40 mm、d23=0.30 mm,交叉耦合逐渐变弱,两个传输零点距离中心频率变远,其幅频特性曲线如图6所示。因此该CT结构在设计交叉耦合滤波器时,只需要调整各个谐振器之间的距离就可以获得所需要的耦合系数,设计和调整均较为方便。
谐振器1和谐振器2之间以及谐振器1和3之间可以实现混合耦合,谐振器1和3之间实现电耦合。所以由前面CT结构理论分析可知,信号的传输通过谐振器1-3实现电耦合,通过谐振器1-2-3实现电耦合和磁耦合,因为相位的不同可以在低频端和高频端各自产生一个传输零点,如图6所示。常规的谐振器设计的CT单元通过相位的变化,只能在高频或者低频端产生一个传输零点,其余的传输零点在无限远处,但是通过平面单螺旋线菱形谐振器设计的CT结构可以在高频和低频端各自产生一个传输零点。根据CT滤波器的设计理论可知,假设本文设计的谐振器之间的直接耦合系数是M12和M23都是正值时,交叉耦合系数M13是负值,所以在通带的高频段产生一个传输零点。由于该特殊结构的平面单螺旋菱形谐振器的复杂耦合形式,使其在通带的低频段也产生了一个传输零点。假设本文设计的谐振器之间的直接耦合系数M12和M23都是正值时,交叉耦合系数M13是负值,所以在通带的低频段产生一个传输零点。调整耦合间距d12、d23可以调整各个谐振器之间的耦合,谐振器1和3之间的交叉耦合是固定电耦合,可通过固定d13的大小,同时通过合理的调整耦合间距d12、d23来调整各谐振器之间的耦合间距就可以单独调整两个传输零点的位置。
相比于CQ结构,该CT结构可以产生一对传输零点,且可以单独可调、可控,方便灵活。调整谐振器之间的耦合间距d12、d23对传输零点的位置的影响,结果如图6所示。最终通过简单的调整d12、d23和d13的大小,就可以获得需要的耦合系数和交叉耦合系数,最终得到结构紧凑、模型美观、性能优异的CT单元,如图5所示。

图5 CT单元

图6 耦合间距与CT单元幅频特性的关系
4 双CT带通滤波器的设计
在ADS电路仿真软件中建立交叉耦合滤波器的LC等效电路模型,等效电路模型中的初始参数采用6阶、切比雪夫响应滤波器的低通原型元件数值,通过调整各个LC等效谐振单元之间的耦合强度获得6阶准椭圆函数滤波器的初始值,最终借助优化算法综合出双CT拓扑结构滤波器的归一化耦合系数矩阵。设计频带为2 850~3 000 MHz双CT结构滤波器,其耦合系数及外部品质因数如表1所示,其中正值代表直接耦合,负值代表交叉耦合。

表1 耦合系数及外部品质因数
采用介电常数为24.1的双面YBCO/LaAlO3/YBCO高温超导薄膜,根据式(3)得半波长约为11.4 mm,从而获得图1b中平面单螺旋线菱形谐振器结构的几何参数值;将外部品质因素eQ值以及滤波器中心频率f0=2 925 MHz代入前节滤波器外部品质因素式(1),求得±90o相对相位带宽90ω±Δ=150 MHz,从而获得滤波器输入输出单元直接馈电方式的抽头位置;由式(2)可计算出各个谐振器之间实现不同耦合系数的几何距离。文献[12]对上述计算过程给予详细介绍。最终获得的单个CT单元如图5所示。
利用图5中所示的CT单元,通过镜像获得对称的第二个CT单元。通过将两个CT单元方便的磁耦合叠加就可以获得双CT结构的高温超导紧凑型滤波器,如图7所示。CT单元之间的耦合设计简单方便,并且可以方便的继续叠加更多的CT单元以获得更优异的带外抑制特性。利用电磁仿真设计得到双CT结构带通滤波器的幅频特性曲线如图8a所示。
该双CT结构带通滤波器结构紧凑,实现S频段小型化滤波器的设计尺寸只有13.5 mm×3.8 mm;由两个CT单元构成的带通滤波器在带外出现两对传输零点,大大提高了带通滤波器的选择性能;如图8b所示,寄生通带在二倍频以外说明该滤波器的阻带特性也很优异,从f0+BW/2到2f0-BW/2的整个阻带内阻带抑制都大于50 dB,能很好地体现该CT单元结构的优势;双CT结构带通滤波器模型在感官上具有立体感的美观效果也是一个亮点,体现出科学与艺术的完美结合。

图7 新颖高温超导紧凑型双CT结构带通滤波器
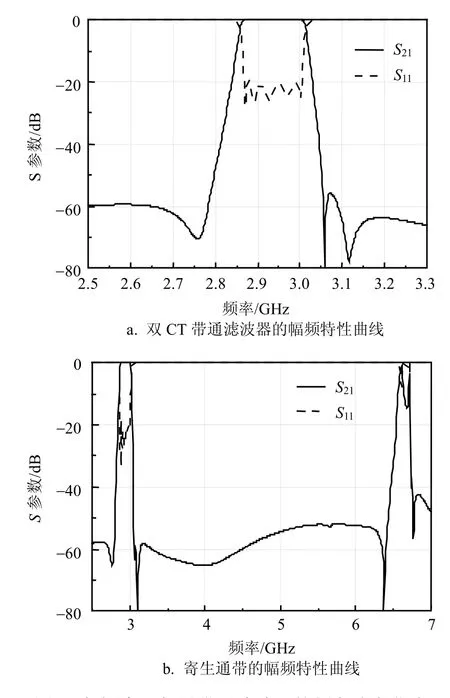
图8 新颖高温超导带通滤波器的频率响应曲线
5 高温超导滤波器的制作与测试

图9 新颖高温超导紧凑型双CT结构带通滤波器实物图
本次选用了性能优越的双面YBCO/LaAlO3/YBCO高温超导薄膜,其在S波段、77 K下测得微波表面电阻RS≤40 µΩ。高温超导滤波器电路采用纳米刻蚀技术制作,双CT结构高温超导滤波器实物如图9所示。采用矢量网络分析仪Agilent 8720B对滤波器进行性能测试,最终的测试结果如图10所示,实测带宽约为150 MHz,带外抑制度大于50 dB,二倍频在6 GHz处,均与设计值吻合良好,尤其是带外抑制特性的实测值与仿真值吻合良好。通带内插入损耗均优于0.27 dB,通带内反射整体≤-12 dB。

图10 新颖高温超导带通滤波器的频率响应测试曲线
6 结束语
设计平面单螺旋菱形谐振器,结合高温超导技术完成紧凑型的双CT结构带通滤波器,具有体积小、选择性能好、很明显的立体感的美观效果等特点。通过合理改变谐振器的相对位置来实现谐振器之间的耦合,引入传输零点提高了滤波器的带外抑制。既实现了滤波器的小型化设计,也避免了使用耦合交叉线,降低了电路对加工工艺的要求。实物经过设计加工与测试证明,该结构实现的双CT结构高温超导滤波器与理论相吻合,具有带外抑制度陡峭、阻带宽,能很好地抑制系统的干扰信号等特点。
[1]郭旭波, 魏斌, 张晓平,等. 采用电容耦合式馈线的高温超导滤波器设计[J]. 微波学报, 2007, 23(S1): 73-76.GUO Xu-bo, WEI Bin, ZHANG Xiao-ping, et al. Design of high-temperature superconducting filter with capacity-coupled feedlines[J]. Journal of Microwaves, 2007,23(S1): 73-76.
[2]SUN L, HE Y. Research progress of high temperature superconducting filters in China[J]. IEEE Transactions on Applied Superconductivity, 2014, 24(5): 1-8.
[3]SAITO A, TESHIMA H, OBARA H, et al. Design and performance of transmit filters using HTS bulk resonators for IMT-advanced applications[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 886-889.
[4]ZHANG T, DU J, GUO Y J, et al. A compact HTS bandpass microstrip filter with novel coupling structure for on-chip integration[J]. Physica C Superconductivity, 2013, 495(8):69-73.
[5]HOU F, ZHANG T, ZHOU L, et al. Cascaded trisection linear-phase filter[C]//IEEE International Conference on Communication Problem-Solving. [S.l.]: IEEE, 2014:584-587.
[6]SEKIYA N, SUGIYAMA S. Design of miniaturized HTS dual-band bandpass filters using stub-loaded meander line resonators and their applications to tri-band bandpass filters[J]. IEEE Transactions on Applied Superconductivity,2015, 25(3): 1-5.
[7]ZHANG T L, YANG K, BU S R, et al. The design of open-loop resonator HTSC linear-phase filter[J]. Cryogenics,2004, 47(7-8): 409-412.
[8]ZHANG T, ZHOU L, YANG K, et al. The research of parallel-coupled linear-phase superconducting filter[J].Physica C Superconductivity, 2015, 519: 153-158.
[9]GAO L, SUN L, LI F, et al. 8GHz narrowband high-temperature superconducting filter with high selectivity and flat group delay[J]. IEEE Transactions on Microwave Theory & Techniques, 2009, 57(7): 1767-1773.
[10]HONG J S, MCERLEAN E P, KARYAMAPUDI B M. A high-temperature superconducting filter for future mobile telecommunication systems[J]. IEEE Proceedings-Microwaves, Antennas and Propagation, 2004, 151(6):491-496.
[11]HONG Jia-sheng, LANCASTER M J. Microstrip filters for RF/microwave applications[M]. [S.l.]: A Wiley-Interscience Publication, 2001.
[12]孔根升. 线性相位接收机前端子系统的研究[D]. 成都:电子科技大学, 2011.KONG Gen-sheng. Study on front end subsystem of linear phase receiver[D]. Chengdu: University of Electronic Science and Technology of China, 2011.

