忆阻超混沌Lü系统的隐藏动力学特性研究
乔晓华,徐 毅,孙玉霞,武花干
(1. 江苏理工学院电气信息工程学院 江苏 常州 213001;2. 常州大学信息科学与工程学院 江苏 常州 213164)
忆阻器因具有非线性和记忆性[1-3],在人工神经网络[4-5]、保密通信[6-7]、计算机内存[8-9]、生物仿真[10-11]等领域有着广泛的应用前景,得到了各领域学者的关注,并取得了丰富的研究成果。特别在电路中,忆阻器作为非线性元件引入电路之后,电路的混沌振荡将变得更加容易实现,其动力学行为更为复杂,所以忆阻混沌电路及其动力学特性研究逐渐成为了学术研究的新热点[12],近年来获得了系列研究成果[13-18]。
隐藏吸引子是近几年新提出的一类吸引子。为了与传统的含有一个或者多个不稳定焦鞍点的混沌系统进行分类,文献[19]将传统的混沌系统定义为自激系统,以区别近年来发现的没有平衡点激发也能产生吸引子的隐藏混沌系统。隐藏吸引子存在于不与任何平衡点的小邻域相交的吸引盆中。为了更好地把握隐藏系统的潜在功能,对于存在隐藏吸引子的系统研究也成为了学术研究的新热点。隐藏吸引子最早是在经典Chua电路中发现的[20],而后学者们利用基于二极管对的非线性滤波电路[21]或者基于二极管桥的广义忆阻器[22]替换Chua电路中的蔡氏二极管,同样发现了这些新型Chua电路具有复杂的隐藏动力学行为。进一步,将实际物理电路中的隐藏动力学行为特点延伸至混沌系统中,通过改造Chua[23]、Lorenz[24-25]、Rabinorich[26]等系统以及忆阻自激振荡系统[27]也产生了具有多稳定性的隐藏混沌或超混沌吸引子。这些电路或系统中除了具有隐藏动力学行为,还存在吸引子的共存现象[27],即不同的初始条件会导致系统轨线分别演化到不同的吸引子上,从而产生共存吸引子即多稳定性[28]。多稳定性现象是非线性动力学系统中普遍存在的一种物理现象,而隐藏吸引子也是一种特殊的多稳定性现象[29]。另外,在文献[30]构建的简单四维系统中,隐藏吸引子有着分别从瞬态超混沌和瞬态周期过渡到稳态混沌的复杂瞬态行为。
已有文献通过在三阶混沌电路或三维混沌系统中引入忆阻[31],得到了一类忆阻混沌或超混沌电路和系统[13-18],但关于忆阻电路和系统产生隐藏超混沌吸引子并具有共存多吸引子的文献报道相对较少[27]。本文通过在经典Lü系统[32]的第二方程中添加一个线性反馈项和一个常数项,并在第一方程中引入一个忆阻,提出了一种新颖的、无任何平衡点的、基于忆阻的改进型Lü系统。改进后的忆阻Lü系统可以产生周期、准周期、混沌和超混沌等复杂隐藏动力学行为,且能在不同的初始条件下产生不同的周期极限环或弱混沌与周期极限环的隐藏多吸引子共存现象。
1 忆阻超混沌Lü系统
1.1 数学模型
从混沌系统的电路实现角度来看,在积分电路的输入项中,电阻表示线性增益,忆阻表示非线性增益,而直流分量,则代表常数项[33]。一种常用的忆阻模型可以描述为[33]:
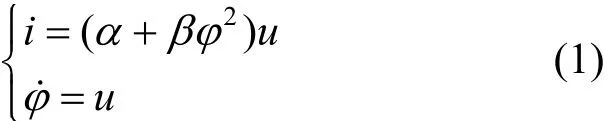
式中,u是忆阻的输入电压变量;i是忆阻的输出电流变量;φ是忆阻的内部磁通变量;α+βφ2是描述忆导变化的非线性函数。
在经典Lü系统的第二方程中添加线性反馈项dx和常数项e,且在第一方程中引入一个式(1)描述的忆阻,即可构建出一种新颖的忆阻超混沌Lü系统,其数学模型表示为:
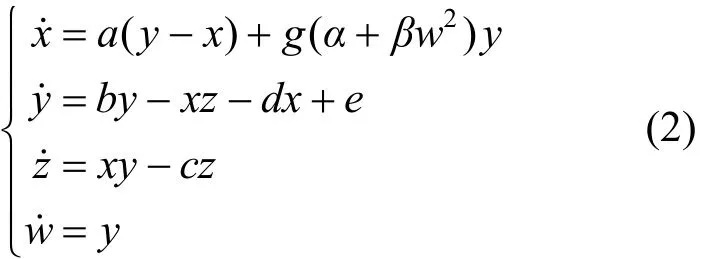
式中,x、y、z和w为4个状态变量;a、b和c为经典Lü系统3个控制参数。为了研究该忆阻Lü系统的隐藏动力学特性,固定系统参数a=36,b=20,c=3,d=5,e=0.1,α=4,β=0.18,选择增益g为系统唯一的可调节参数。
1.2 基本动力学分析
通过忆阻Lü系统的方程式(2)可以得到:
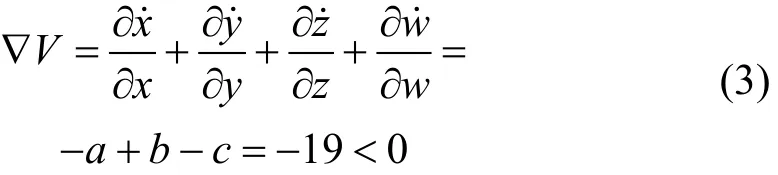
由式(3)可知,∇V<0,说明系统是耗散的,同时也说明Lü系统的改进和忆阻的引入没有改变原经典Lü系统的耗散度。
令x˙ =y˙ =z˙ =w˙ =0,显然式(2)不存在任何数学解,即所提出的忆阻Lü系统不存在任何平衡点,完全不同于具有3个平衡点的经典Lü系统。根据隐藏吸引子的定义[19-29],无平衡点的忆阻Lü系统所产生的周期极限环、准周期极限环、混沌吸引子和超混沌吸引子均是隐藏的。
系统(2)的雅克比矩阵为:
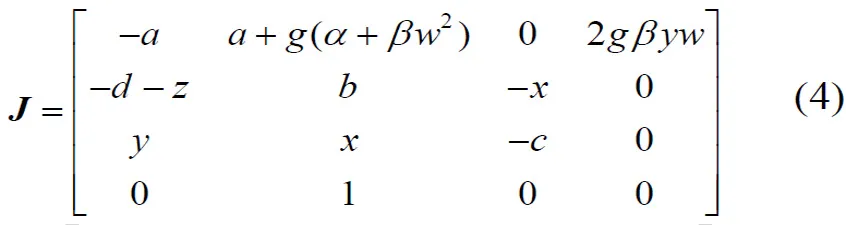
相应的特征方程为:
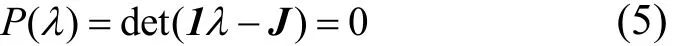
基于式(4),利用Wolf算法可计算得到忆阻Lü系统的李雅普诺夫指数。
1.3 隐藏动力学行为
以忆阻的增益g作为调节参数,设置初始条件为(1,0,1,0),随忆阻的增益g在区域[6,16]变化的李雅普诺夫指数谱如图1a所示,与之对应的状态变量z的分岔图如图1b所示。
当忆阻增益g=6时,LE1=0,其余3个李雅普诺夫指数LE2、LE3、LE4<0,忆阻Lü系统处于周期态。在6<g<7.69内,忆阻Lü系统处于周期态或弱混沌态。当g=7.69且继续增大时,LE1、LE2=0,LE3、LE4<0,忆阻Lü系统从周期态过渡到准周期态。随着忆阻增益的继续增大,在8.3<g<9.02内,LE1>0、LE2=0和LE3、LE4<0,忆阻Lü系统处于相对稳定的混沌参数区间。当忆阻增益继续增大时,LE1、LE2开始出现抖动,直到g=10.09时结束,忆阻Lü系统开始由混沌状态转移到超混沌状态。在10.09<g<14.55内,LE1>0、LE2>0、LE3=0和LE4<0,忆阻Lü系统处于超混沌状态。自g=14.55且逐步增大至15时,忆阻Lü系统交替处于超混沌状态或混沌状态。
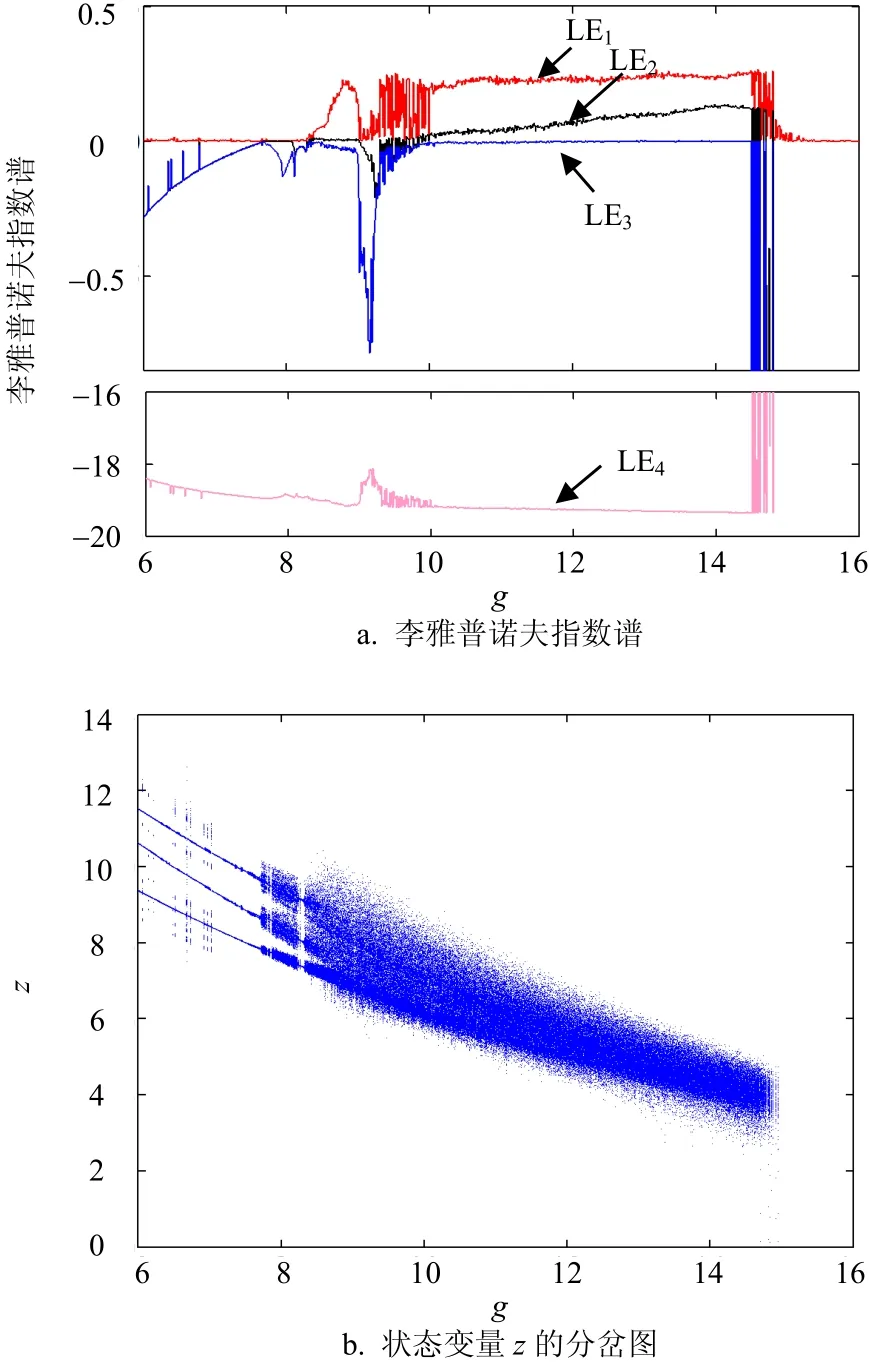
图1 系统(2)随忆阻增益g变化的隐藏动力学行为
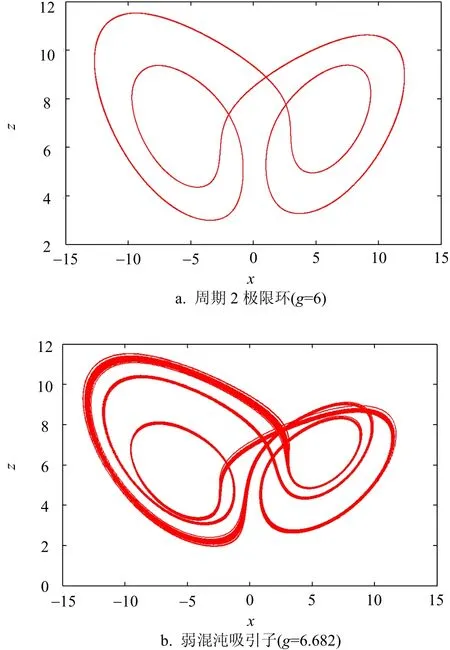
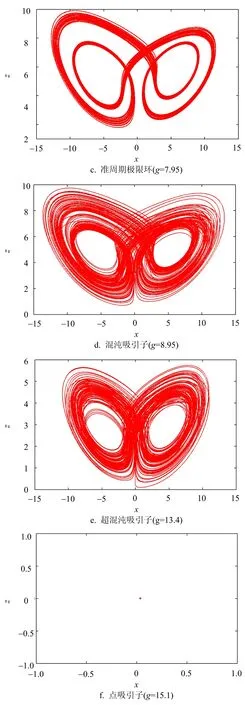
图2 系统(2)在x-z平面上的相轨图
在g>15之后,LE1=0,其余3个李雅普诺夫指数LE2、LE3、LE4<0,忆阻Lü系统迅速地收敛到一个点吸引子。在各参数区间选取典型的参数值,忆阻Lü系统在x-z平面上典型的相轨图如图2所示。
此外,图3给出了典型超混沌吸引子在4个平面上的相轨图。
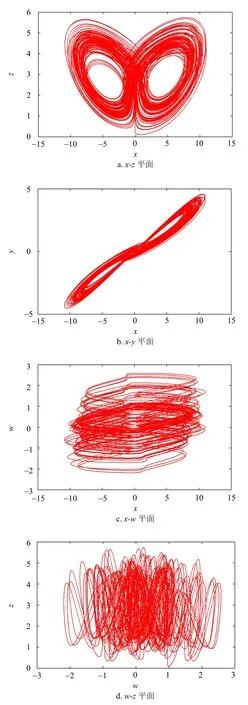
图3g=13.4,系统(2)典型超混沌吸引子的相轨图
2 隐藏多吸引子行为
设定忆阻Lü系统的初始条件分别为(1,0,1,0)、(1,3,1,0)和(1,3,1,1),对应的系统运行轨迹分别用蓝色、绿色和红色3种颜色呈现。当g在[5.959,5.973]和[6.9,7.0]区间变化时,3种不同初始条件的状态变量z的分岔图分别如图4和图5所示。由图4和图5分析可知,当g在[5.959,5.973]区间变化时,系统的运行轨迹因初始条件的不同而出现了3个不同的周期极限环共存现象,且3个极限环均有不同的李雅普诺夫指数谱;当g在[6.9,7.0]区间变化时,系统的运行轨迹因初始条件的不同而出现了隐藏弱混沌和周期极限环共存的现象。图4和图5的结果说明,忆阻Lü系统产生了3个吸引子共存或弱混沌与周期极限环共存的多稳定性现象。
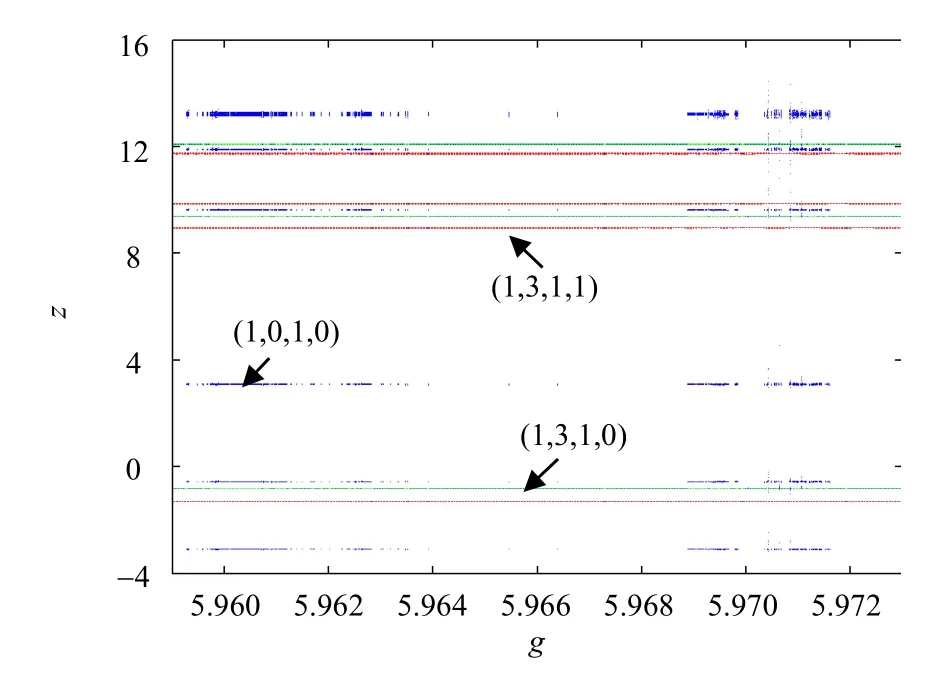
图4 在g∈ [5.959,5.973]内的不同初始条件下,系统(2)的隐藏多吸引子分岔行为
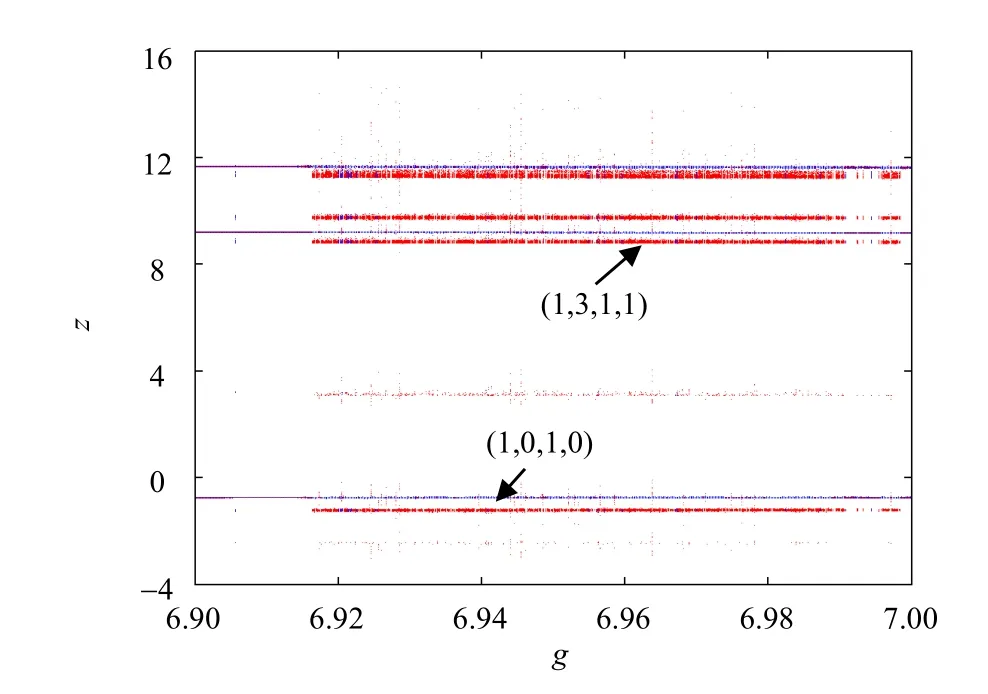
图5 在g∈[6.9,7.0]内不同初始条件下,系统(2)的隐藏多吸引子分岔行为
当选忆阻增益g=5.96时,忆阻Lü系统系统(2)是周期的,可展示出3个隐藏极限环的共存现象,在x-z和x-w平面上的投影如图6所示,红色轨迹则表示从初始条件为(1,3,1,1)出发的运行轨迹,蓝色轨迹则表示从初始条件为(1,0,1,0)出发的运行轨迹,绿色轨迹表示从初始条件为(1,3,1,0)出发的运行轨迹。其中,红色隐藏周期3极限环的4个李雅普诺夫指数分别为:LE1=0,LE2=-0.225 5,LE3=-0.226 4,LE4=-18.51,蓝色隐藏周期3极限环的4个李雅普诺夫指数分别为:LE1=0,LE2=-0.297 6,LE3=-0.299,LE4=-18.37,绿色隐藏周期2极限环的4个李雅普诺夫指数分别为:LE1= 0,LE2=-0.298 4,LE3=-0.299,LE4=-18.36。当忆阻增益g=6.936时,忆阻Lü系统(2)是弱混沌的,或是周期的,完全取决于系统(2)的初始条件。共存的隐藏弱混沌吸引子与隐藏周期极限环的相轨图如图7所示。其中,红色轨迹表示从初始条件(1,3,1,1)出发的运行轨迹,为弱混沌带,其4个李雅普诺夫指数分别为:LE1=0.010 35,LE2=-0.071 47,LE3=-0.154 6,LE4=-18.78,而蓝色轨迹则表示从初始条件(1,0,1,0)出发的运行轨迹,为周期2极限环,其4个李雅普诺夫指数分别为:LE1=0,LE2=-0.083 78,LE3=-0.085 5,LE4=-18.84。
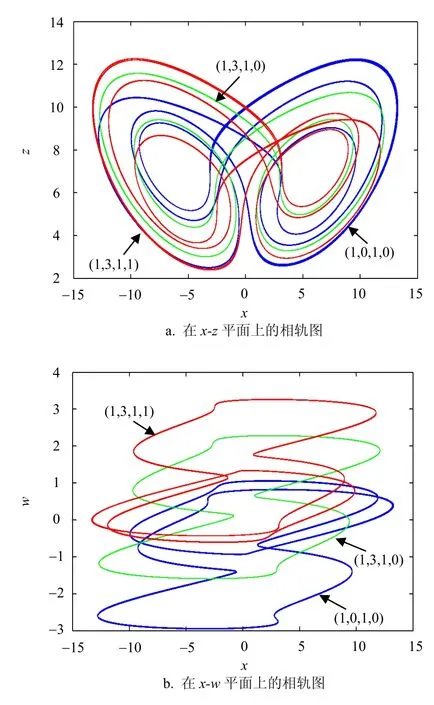
图6 系统(2)的3个不同周期极限环共存现象
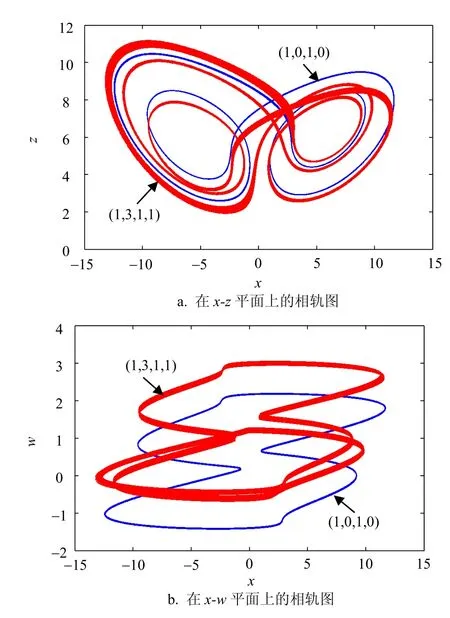
图7 系统(2)弱混沌吸引子和周期极限环共存现象
3 硬件电路验证
采用电阻、电容、运算放大器和模拟乘法器等分立元器件构建的模拟电子电路实现本文提出的忆阻超混沌Lü系统。
在电路制作中,选用型号OP07CP作为运算放大器,型号AD633JN作为模拟乘积器,两者的工作电压动态范围分别为±16 V和±10 V。考虑到实际电路的输出信号幅度不应大于电路器件的饱和电压,也不应过小而导致信号失真。根据前述数值仿真结果,可知超混沌吸引子和共存多吸引子的x、y、z、w状态变量的动态范围分别在±15、±5、0~12、±4 V,因此,需要对系统(2)的状态变量进行线性缩放如下:
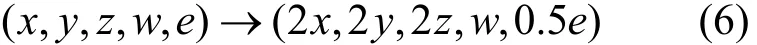
选择时间尺度因子为k=1/(RC)。系统(2)经过时间尺度因子转换并进行状态变量线性缩放后的电路方程为:
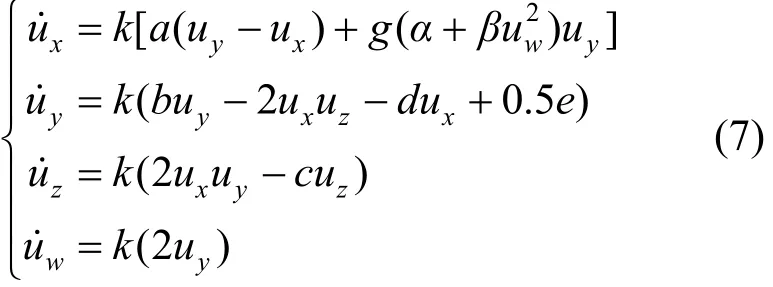
式中,ux、uy、uz和uw表示电路中4个电容两端的电压,分别对应于x、y、z和w状态变量。
基于式(7)的电路方程,可设计并实现的电路原理图如图8所示。选择时间尺度因子k中的R=36 kΩ和C=100 nF。与系统(2)比较,可得图8中电容值均为C1=C2=C3=C4=C=100 nF,电阻值分别为R1=R2=R/a=1 kΩ,R3=R/c=12 kΩ,R4=R5=R/20=1.8 kΩ,R6=R/b=1.8 kΩ,R7=R/d=7.2 kΩ,R8=R9=R=36 kΩ,R10=R/2=18 kΩ和R13=2R=72 kΩ。此外,电阻R11和R12是联动可调的,其参数值分别为:R11=R/gα,R12=R/100gβ。实现图8的硬件实验电路图如图9所示。
采用Agilent DSO7054B数字示波器捕捉图9硬件实验电路测试结果,其中4个节点电压测量点被标记为ux,uy,uz,uw。在典型电路参数下,当g=13.4时,忆阻超混沌Lü系统硬件电路输出的隐藏超混沌吸引子在ux-uz、ux-uy、ux-uw和uw-uz平面上的相轨图分别如图10a~图10d所示。进一步地,当g=5.96时,联动可调电阻的参数值分别固定为:R11=1 510 Ω,R12=335.5 Ω,从数字示波器上可捕捉到的3个共存隐藏极限环在ux-uz和ux-uw平面上的相轨图分别如图11a和图11b所示。
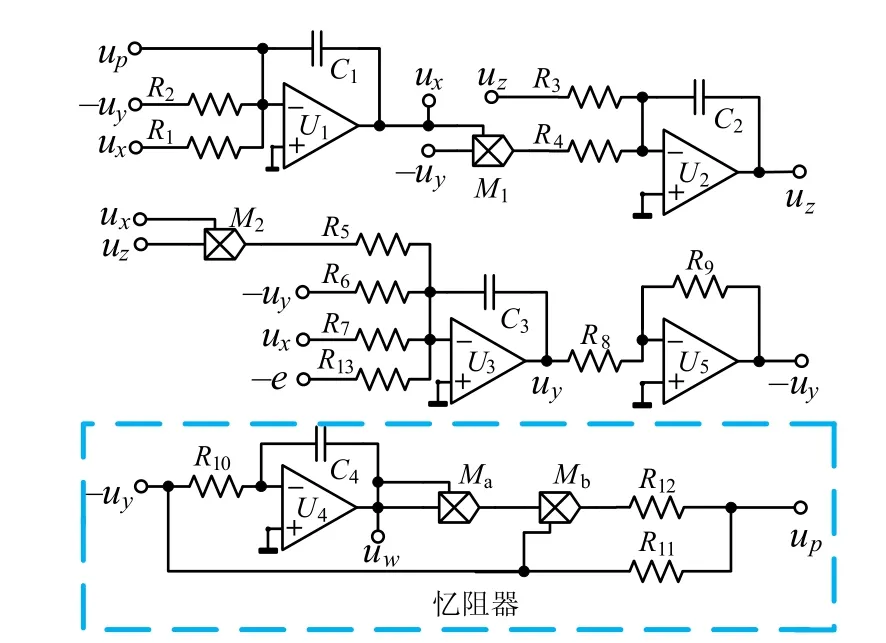
图8 系统(2)的实验电路原理图

图9 系统(2)的硬件实验电路图
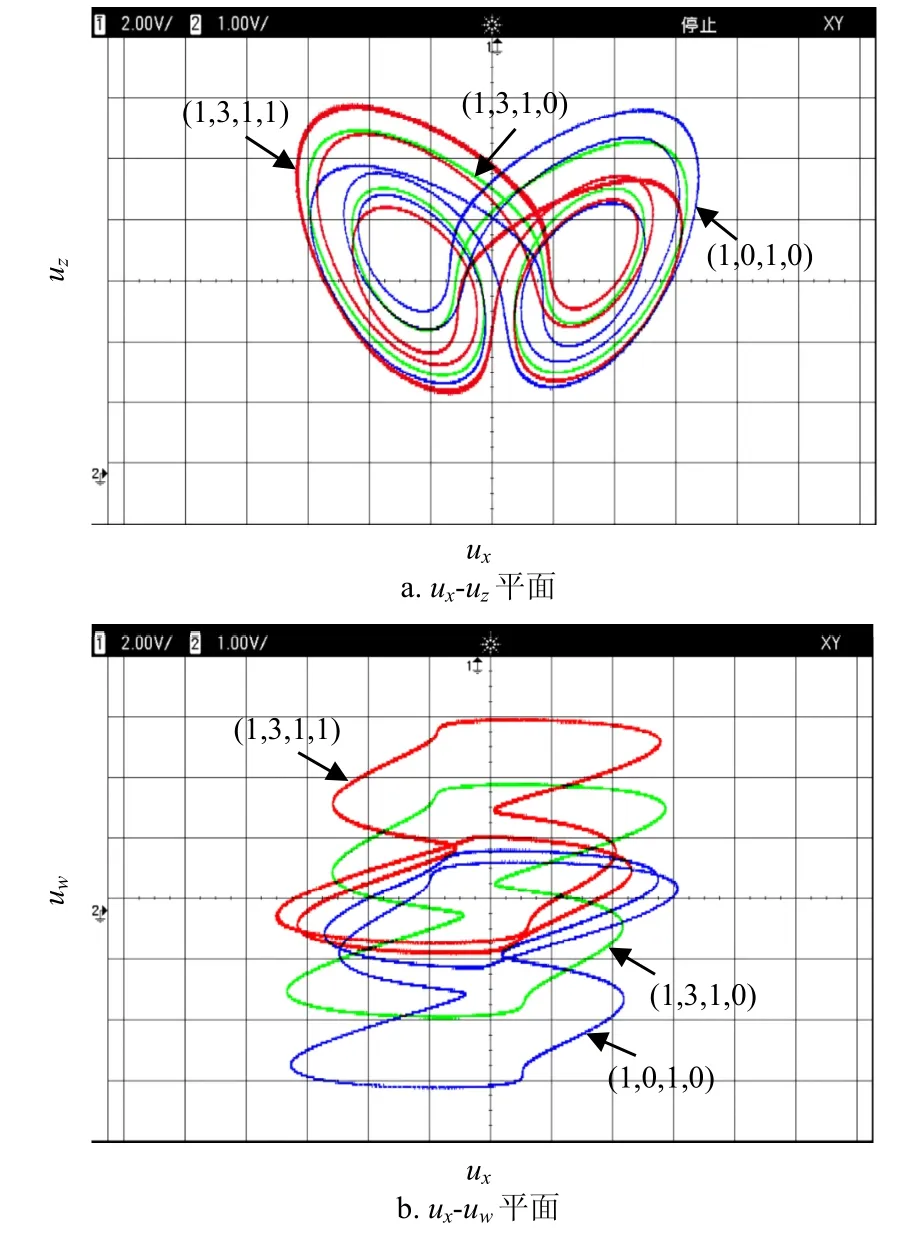
图11g=5.96,系统(2)在不同平面上实验捕捉到的相轨图
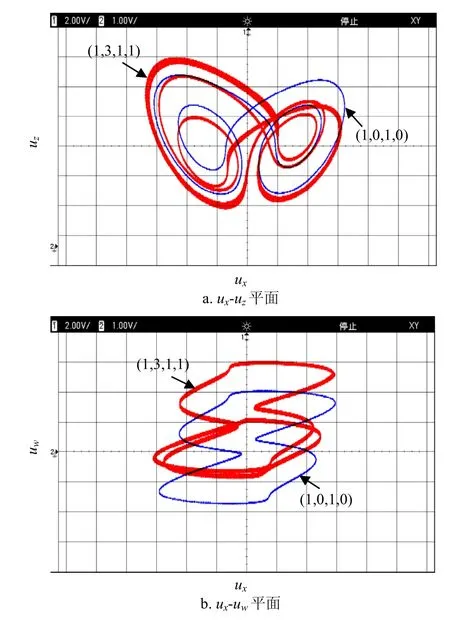
图12g=6.936,系统(2)在不同平面上实验捕捉到的相轨图
当g=6.936时,联动可调电阻的参数值分别固定为:R11=1 297.5 Ω,R12=288.3 Ω时,从数字示波器上可捕捉到的共存隐藏弱混沌吸引子与隐藏周期极限环在ux-uz和ux-uw平面上的相轨图分别如图12a和图12b所示。这里,不同颜色标注的实验波形是通过不断接通和断开图9硬件电路的供电电源随机捕捉到的。分别与图3、6和7的数值仿真结果相比较,可见电路实验结果与数值仿真结果完全一致,从而由硬件电路验证了忆阻超混沌Lü系统的隐藏超混沌吸引子和共存多吸引子的存在性。
4 结束语
通过改进经典Lü系统并引入磁控忆阻器,提出了一种新颖的基于忆阻的改进型超混沌Lü系统。不同于传统意义上的自激混沌系统,该忆阻系统因无任何平衡点,故所产生的吸引子均属于隐藏吸引子。通过调节忆阻的增益可控制系统分别处于超混沌、混沌、准周期或周期等振荡状态。特别地,在不同初始条件下,忆阻超混沌Lü系统会呈现3个不同周期极限环的共存现象,以及弱混沌吸引子和周期极限环的共存现象,说明新系统存在多稳定性。最后,开展了电路实验验证,测量结果较好地验证了理论分析和数值仿真结果。
[1]CHUA L O. Memristor-the missing circuit element[J]. IEEE Trans Circ Theory, 1971, 18(5): 507-519.
[2]STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found[J]. Nature, 2008, 453: 80-83.
[3]WANG X B, CHEN Y R. Spintronic memristor through spin-torque-induced magnetization motion[J]. IEEE Electron Device Letters, 2009, 30(3): 294-297.
[4]BAO G, ZENG Z G. Multistability of periodic delayed recurrent neural network with memristors[J]. Neural Computing & Applications, 2013, 23(7-8): 1963-1967.
[5]PERSHIN Y V, DI V M. Experimental demonstration of associative memory with memristive neural networks[J].Neural Networks, 2010, 23(7): 881-886.
[6]HO Y, HUANG G M, LI P. Dynamical properties and design analysis for nonvolatile memristor memories[J]. IEEE Transactions on Circuits & Systems I, 2011, 58(4): 724-736.
[7]WEN S, ZENG Z, HUANG T. Adaptive synchronization of memristor-based Chua’s circuits[J]. Physics Letters A, 2012,376(4): 2775-2780.
[8]CONG J, XIAO B J. MrFPGA: a novel FPGA architecture with memristor-based reconfiguration[C]//Proceedings of the 2011 IEEE/ACM International Symposium on Nanoscale Architectures. San Diego, CA: IEEE, 2011.
[9]PERSHIN Y V, VENTRA M D. Practical approach to programmable analog circuits with memristors[J]. IEEE Transactions on Circuits & Systems I, 2010, 57(8):1857-1864.
[10]WILLIAMS S. How we found the missing memristor[J].IEEE Spectrum, 2008, 45(12): 28-35.
[11]PERSHIN Y V, FONTAINE S L, VENTRA M D.Memristive model of amoeba learning[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80(2 Pt 1): 021926.
[12]TALUKDAR A, RADWAN A G, SALAMA K N. Non linear dynamics of memristor based 3rd order oscillatory system[J]. Microelectronics Journal, 2012, 43(3): 169-175.
[13]BAO B C, XU J P, ZHOU G H, et al. Chaotic memristive circuit: Equivalent circuit realization and dynamical analysis[J]. Chinese Physics B, 2011, 20(12): 109-115.
[14]BAO B C, LIU Z, XU J P. Transient chaos in smooth memristor oscillator[J]. Chinese Physics B, 2010, 19(3):158-163.
[15]SAHA P, SAHA D C, RAY A, et al. Memristive non-linear system and hidden attractor[J]. European Physical Journal Special Topics, 2015, 224(8): 1563-1574.
[16]杨芳艳, 冷家丽, 李清都. 基于Chua电路的四维超混沌忆阻电路[J]. 物理学报, 2014, 63(8): 080502.YANG Fang-yan, LEN Jia-li, LI Qing-du. The 4-dimensional hyperchaotic memristive circuit based on Chua’s circuit[J]. Acta Physica Sinica, 2014, 63(8):080502.
[17]LI Q D, ZENG H, LI J. Hyperchaos in a 4D memristive circuit with infinitely many stable equilibria[J]. Nonlinear Dynamics, 2015, 79(4): 2295-2308.
[18]LI Q D, HU S, TANG S, et al. Hyperchaos and horseshoe in a 4D memristive system with a line of equilibria and its implementation[J]. International Journal of Circuit Theory& Applications, 2014, 42(11): 1172-1188.
[19]LEONOV G A, KUZNETSOV N V, MOKAEV T N.Hidden attractor and homoclinic orbit in Lorenz-like system describing convective fluid motion in rotating cavity[J]. Communications in Nonlinear Science &Numerical Simulation, 2015, 28(1-3): 166-174.
[20]LEONOV G A, KUZNETSOV N V, VAGAITSEV V I.Localization of hidden Chua’s attractors[J]. Physics Letters A, 2011, 375(23): 2230-2233.
[21]BAO B C, HU F W, CHEN M, et al. Self-excited and hidden attractors found simultaneously in a modified Chua's circuit[J]. International Journal of Bifurcation &Chaos, 2015, 25(5): 1550075.
[22]CHEN M, LI M Y, YU Q, et al. Dynamics of self-excited attractors and hidden attractors in generalized memristor-based Chua’s circuit[J]. Nonlinear Dynamics,2015, 81(1-2): 215-226.
[23]LI Q D, ZENG H Z, YANG X S. On hidden twin attractors and bifurcation in the Chua’s circuit[J]. Nonlinear Dynamics, 2014, 77(1-2): 255-266.
[24]LI C B, SPROTT J C. Coexisting hidden attractors in a 4-D simplified lorenz system[J]. International Journal of Bifurcation & Chaos, 2014, 24(3): 1450034.
[25]LEONOV G A, KUZNETSOV N V, MOKAEV T N.Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion[J].The European Physical Journal Special Topics, 2015,224(8): 1421-1458.
[26]WEI Z C, YU P, ZHANG W, et al. Study of hidden attractors, multiple limit cycles from Hopf bifurcation and boundedness of motion in the generalized hyperchaotic Rabinovich system[J]. Nonlinear Dynamics, 2015, 82(1):1-11.
[27]包涵, 包伯成, 林毅, 等. 忆阻自激振荡系统的隐藏吸引子及其动力学特性[J]. 物理学报, 2016, 65(18):180501.BAO Han, BAO Bo-cheng, LIN Yi, et al. Hidden attractor and its dynamical characteristic in memristive self-oscillating system[J]. Acta Physica Sinica, 2016,65(18): 180501.
[28]PISARCHIK A N, FEUDEL U. Control of multistability[J].Physics Reports, 2014, 540(4): 167-218
[29]DUDKOWSKI D, JAFARI S, KAPITANIAK T, et al.Hidden attractors in dynamical systems[J]. Physics Reports,2016, 637: 1-50.
[30]DANG X Y, LI C B, BAO B C, et al. Complex transient dynamics of hidden attractors in a simple 4D system[J].Chinese Physics B, 2015, 24(5): 270-274.
[31]BAO B C, ZOU X, LIU Z, et al. Generalized memory element and chaotic memory system[J]. International Journal of Bifurcation & Chaos, 2013, 23(23): 50135.
[32]LÜ J H, CHEN G R. A new chaotic attractor coined[J].International Journal of Bifurcation & Chaos, 2002, 12(3):659-661.
[33]BAO B C, BAO H, WANG N, et al. Hidden extreme multistability in memristive hyperchaotic system[J]. Chaos Solitons & Fractals, 2017, 94: 102-111.

