基于改进多层次灰色评价法的项目组合评价研究

董　欣　白思俊　刘海斌　郭云涛

(西北工业大学 管理学院，陕西 西安　710129)

0　引言

多层次灰色评价法是一种从评价等级的模糊性、不明确性出发，应用于对象复杂、层次多且不易量化的系统的评价方法，被广泛应用于社会、经济系统的评价，比如汪侠等将其用于对旅游者感知的综合评价，苏菊宁等研究了物流外包中的物流合作伙伴评价选择问题，任宏等对建筑施工企业信息化能力进行了评价。项目组合的评价信息不仅分散而且具有模糊性，评价结果容易受到人为因素的影响。因此，多层次灰色评价法同样适用于对项目组合的评价。郭鹏等利用灰色多层次综合评价法对棕地再开发项目进行评价，计算各开发方案间的灰色关联系数以构建灰色评价矩阵，提高了评价结果的准确性；王家远等基于可持续发展的视角构建了住宅建设项目的综合评价指标体系，运用多层次灰色评价法建立了综合评价模型。但是，现有的研究并没有指出白化权函数存在的集中趋势，忽略了集中趋势会使得综合评价值之间的差异减少，不利于领导者做出正确的选择。本文将多层次灰色评价法引入项目组合评价问题中，并针对多层次灰色评价法的不足进行改进，提出了修正函数，以减少白化权函数的集中趋势，为项目组合评价提供一种新的思路，帮助企业的决策者更好地做出项目组合的选择。

1　多层次灰色评价法的不足及改进

1.1　多层次灰色评价法的不足

传统的多层次灰色评价法的不足之处在于白化权函数存在集中趋势，导致综合评价值之间的差异被弱化，不能满足项目组合评价的需求。这里用实际例子加以说明。

简化处理：对于项目组合方案，把指标体系简化为一个指标V，其权重W=1；只有一个专家为评价指标打分，分值为x；经过白化权函数处理后的综合评价值为Z，称为实际值。

1.1.1实例的引入

将评价指标划分4个等级，并分别赋值1、2、3、4分。对于项目组合方案，设评价专家的打分值为xs。相应设置4个评价灰类，序号为e(e=1,2,3,4)。设评价灰类的灰数为⊗1，⊗2，⊗3，⊗4，其对应的白化权函数为f1，f2，f3，f4。对4个评价灰类等级赋值1、2、3、4，得到评价等级值化向量G=(1，2，3，4)。

以一组典型的评价灰类为例，其白化权函数的解析式如下：

设方案S的综合评价值为Zs，计算公式为

Zs=W·Rs·GT=

(1)

式中：

W——评价指标V的权重向量；

GT——评价等级值化向量的转置矩阵；

Rs——方案S的灰色评价权向量。

图1　综合评价值的集中趋势

对两个函数图像比较分析我们发现，两线相交于O点(3.179，3.179)。在O点左侧区域，实际值大于参考值，x越小二者偏差越大；在O点右侧区域，实际值小于参考值，x越大二者偏差也越大。与灰色的直线相比，黑色曲线的斜率更小，这说明综合评价值的实际值趋于集中，数值之间的差异性被弱化。由于各评价灰类在中间灰色区域的叠加，导致中间等级的灰色评价权高于两端区域的评价权。最终的结果是，综合评价值向中间靠拢，产生“集中效应”。这种“集中效应”弱化了评价结果之间的差异，令决策者难以做出选择和判断。

1.1.2集中趋势的量化

首先，明确Zs(x)的实际应用区间为[1，4]。可看出综合评价值集中程度是与偏差程度呈正相关的，所以可以用实际值与参考值的偏差间接地反映实际值的集中程度。设偏差函数Ds(x)( Deviation)，它表示综合评价值的实际值偏离参考值的程度，计算公式如下：

(2)

1.2　修正函数的提出及检验

1.2.1修正函数的提出

为了减弱综合评价值的实际值的集中趋势，对实际值函数Zs(x)做整体的旋转变换，调整其斜率以接近参考值函数。由于Zs(x)的函数图像是曲线，旋转变换的计算过程较复杂，故选用一种简化的方法间接得到一个近似结果。旋转变换的具体操作步骤如下：

1.运用EXCEL软件对区间[1，4]上的Zs(x)曲线做线性回归，得到线性回归方程：

y=0.502 7x+1.615 8 (1≤x≤4)

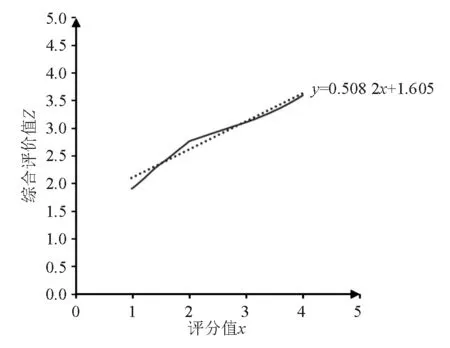
图2　Zs(x)的线性回归

2.求回归线段的中点坐标：取区间[1，4]的中点x=2.5，代入线性回归方程得y=2.8763，所以中点坐标为(2.5,2.8763)；

3.以中点为不动点对回归线段做旋转变换：设中点(2.5,2.8763)为不动点，对回归直线进行旋转，使其斜率为1，得直线y′=x+0.3763，变换方程如下：

(3)

4.将变换方程应用于Zs(x)，得到变换后的曲线Zs′(x)：

曲线Zs′(x)如图3的灰色曲线所示：

图3　Zs(x)的修正变换

5.定义修正函数Cs(x)(Correction)：

对于具体的x0，其对应的修正系数为cs(x0)。在求出各综合评价值的实际值后，再乘以相应的修正系数，即可增加各综合评价值的离散程度，减少综合评价值的集中趋势。

1.2.2白化权函数的检验

选取统计学的两个基本概念——期望值、方差，来描述偏差系数的平均大小和离散程度，定义平均偏差系数和偏差系数方差。由于偏差系数有正负之分，取偏差系数的绝对值进行计算。设白化权函数的实际应用区间为[a,b]，取a=min (g1，g2，L，gE)，b=max (g1，g2，L，gE)，即评分的最小值和最大值。

(5)

设偏差系数d在区间[a,b]上的概率分布函数P(x)为

(6)

对于某个具体的x值，它所对应的偏差系数为p(x)。

定义偏差系数方差σ2，表示偏差系数在实际应用区间内的离散程度：

(7)

2　项目组合评价的多层次灰色评价步骤

2.1　评分等级标准和评价灰类的确定

将评价指标的评分等级划分为4级，分别赋值1，2，3，4分。当评价指标介于两相邻等级之间时，则赋值1.5，2.5或3.5。

设定4个评价灰类，序号为e(e=1,2,3,4)，分别对应于“差”“中”“良”“优”。各评价灰类的灰数为⊗1，⊗2，⊗3，⊗4，对应的白化权函数为f1,f2,f3,f4。最后对评价灰类进行赋值，得到评价灰类等级值化向量G=(1,2,3,4)。在这种情况下，将实际值函数修改为：

(8)

2.2　评价指标的赋权

本文从现有的国内外文献中总结了基于平衡记分卡的战略评价指标，采用德尔菲法来实现关键指标向项目型指标的转化，并且在指标体系中增加了“项目间的协同度”这一指标来衡量项目组合内部的关联性，最终得到5个一级指标，14个二级指标(见表1)。

表1　项目组合评价指标体系

本文采用乘法合成法的组合赋权方式，设层次分析法所确定的指标权重为αi，熵值法确定的指标权重为βi，组合赋权法所得权重为wi。乘法合成法的计算公式如下：

(9)

因此，得到二级评价指标的权重向量W：

W=(ω11，ω12，ω21，ω22，ω31，ω32，ω33，ω41，ω42，ω43，ω44，ω51，ω52，ω53)

2.3　评价样本矩阵

设有p个评价专家对项目组合进行评价，序号为k(k=1,2,L,p)。对于项目组合Pt，设第k个评价专家给评价指标Vij的打分值为xijk(i=1,2,3,4,5；j=1,2,L,ni；k=1,2,L,p)，xijk构成了项目组合Pt的评价样本矩阵：

2.4　灰色评价权矩阵

(10)

(11)

2.5　名义修正系数矩阵

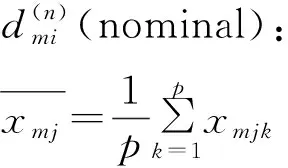
(12)

(13)

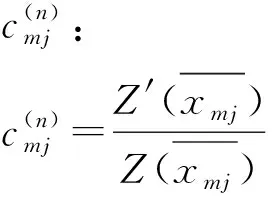
(14)

(15)

2.6　综合评价值的计算

对于项目组合Pt，确定好灰色评价权矩阵R、二级评价指标权重向量W′、名义修正系数矩阵C(n)及评价等级值化向量G后，即可计算综合评价值Z：

Z=W′·C(n)·R·GT

(16)

3　实例研究

3.1　企业背景介绍

X公司是我国一家以民用飞机设计、制造为主业的项目型企业，决策层决定采用项目组合的研发管理模式来实现企业的战略目标。

经X公司高层领导和专家的决策，已经从8个备选项目(p1,p2,p3,p4,p5,p6,p7,p8)中选择、制定了3个项目组合方案P1,P2,P3。其中，P1=(p1,p2,p4,p7)，P2=(p3,p4,p+,p7)，P3=(p2,p5,p6,p8)，选择能最大化实现组织战略目标的项目组合方案进行实施。

3.2　评价模型应用

(1)评价等级标准和评价灰类的确定。根据前文给出的评分等级标准，相应地确定4个评价灰类，灰类的序号为e(e=1,2,3,4)，给出灰类的灰数⊗e所对应的白化权函数分别为fe，如下所示：

在实际应用区间[1，4]，实际值函数的解析式为

根据公式(2)求解偏差函数：

根据公式(5)求解平均偏差系数：

根据公式(6)先计算出偏差系数的分部概率函数P(x)，再根据公式(7)计算偏差系数方差：

(2)评价指标权重的确定。运用层次分析法得到判断矩阵，计算各评价指标的相对重要度，并进行一致性检验。对于战略目标V而言，一级评价指标Vi的相对重要度如表2所示。

表2　判断矩阵

运用层次分析法和熵值法分别得到各评价指标权重，根据公式(9)得到指标的组合权重如表3所示。

表3　组合赋权法得到的各指标相对重要度

最后，求各评价指标Vij相对战略目标的权重，得到Vij的权重向量W：

W=(0.091;0.018;0.234;0.082;0.012;0.110;0.089;0.027;0.040;0.072;0.010;0.056;0.037;0.061)

(3)评价样本矩阵。对于3个项目组合方案P1，P2，P3，邀请5位项目专家分别为指标打分，得到三个评价样本矩阵X1,X2,X3：

(4)灰色评价权矩阵。得到评价样本矩阵X1,X2,X3后，通过计算得到各个评价指标的灰色评价权向量，最后汇总构成灰色评价权矩阵R1,R2,R3：

(5)名义修正系数矩阵。根据修正函数的定义，代入白化权函数得到修正函数的解析式：

根据公式(12)、(14)计算出各项指标的名义修正系数，见表4。

表4　项目组合方案 P1，P2 ，P3的各名义修正系数

(6)综合评价值

根据计算公式(16)，计算项目组合P1,P2,P3的综合评价值，见表5。

表5　各评价维度的评价值

3.3　评价结果比较

运用传统的多层次灰色评价法计算综合评价值，将所得到结果与改进方法得到的结果做比较，见表6。

表6　改进方法与传统方法所得结果的比较

通过表6可以发现前者数据之间的差异大于后者，说明改进方法确实增加了综合评价值之间的差异性，更有利于决策者作出分析和判断。