基于偏微分方程的多变量自适应优化

殷 珊

(新疆轻工职业技术学院， 乌鲁木齐 830021)

目前，在大多数归纳学中，几乎都可以获得网络簇的解。从网络簇分类器方面看，拥有的显著优点大致为：在对网络簇进行测试时，网络簇一直沿着分支执行；网络簇可以提供具体关于特殊案列的种类顺序决策方案的详细说明，[1]同时，人们更加喜欢使用简单的网络簇进行测试。主要的原因在于使用这类网络簇更加有利于加深对决策的理解和进一步认识。大多数网络簇只是单个节点的单一功能，即单变量网络簇。ID3、[2]AQ1、[3]ASSISTANT[4]和 GREEDY3 及 GROVE，[5]这种限制使得难以或不可能表达许多复杂的概念。

在多变量网络集群优化问题中，最为核心的部分是如何实现多变量测试的充分优化。主要涵盖了如下几方面的内容：一是在多变量测试中，如何确定初始特征？二是通过选择确定的特征，如何实现对多变量检验的优化。文章首先就偏微分方程的相关理论以及相对核等概念进行了阐述，以此为基础对于如何选择初始特征进行了分析；然后对优化多变量网络集群算法进行了描述；最后通过一个案例，采用对比法分析了多变量网络簇与单变量网络簇方法，并且针对几种多变量网络簇展开了对比论述。

一、多变量网络簇的自适应优化算法

（一）特征的选择

对于特征与等价关系而言，两者之间是对等的，即彼此是可以互相替代的。因此，对两个概念并未进行严格的区分。

U代表了一个感兴趣的对象集合，也叫做论域，R是U上的一个等价关系，U/R则代表了R于上U得到的划分，则代表了R等价类中包含了 x的集合，x∈U。（U，R）序列称为近似空间。对于任意的子集X⊆U，也叫做概念。对于每个概念X可以定义如下：

RX是通过那些现有R知识下属概念X元素得到的集合，并且依据等价关系的不同得到了两个正区域定义：

POSP（Q）代表了U中能够依据知识P进行肯定划分，最终归为U/Q类的元素集合。

此时U假定为一个论域，而P、Q则为基于U上定义的两个等价关系族，并且，如果此时其中的某个等价关系R∈P能够满足下式中的条件，则可将其判定为Q-不必要。

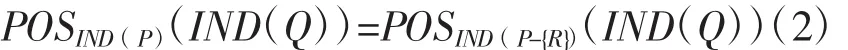
成立，（其中所有交叉等价关系）也是等价关系，并且被称为不可分辨关系。

COREQ（P）代表了 P 的 Q-核，指的是 P 中全部的Q-必要等价关系中，所有的必要等价关系集合。

当P与Q分别表示条件特征与决策特征时，它不会改变原始信息系统的决定，并且当与信息系统的条件特征和决策特征不同时，删除的核的特征将会对原始信息特征产生影响，导致其发生变化，因此，在决策中核的特性是具有十分重要的作用的。因此，在进行多变量测试优化时，是依据相对核的特性来作为自适应优化特征的。

（二）泛化界定

如何利用所选功能实现对多变量测试的有效优化？经过上述分析后，能够发现，如果采用的是所选特征的简单组合，则最终可能会产生数据的过拟合。因此，我们定义出了另一种与等价概念相对的泛化等价关系。

定义1.P、Q为U上两个等价关系族，且

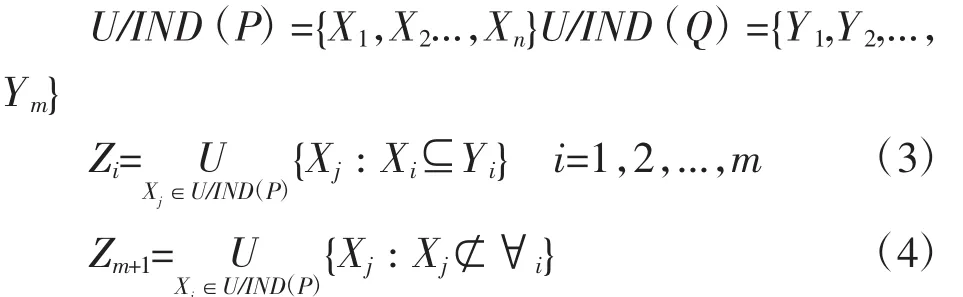
则称{Z1，Z2，...，Zm+1}在 U 上确定的等价关系为P相对Q的泛化，以GENQ（P）表示。

通过下述命题可对上述定义和理性进行证明。

命题 1.{Z1，Z2，...，Zm+1}为 U 上的一个划分，其中 Zi，i=1，2，...，m+1 由（3）（4）式定义。

证明：从Zi的定义可知

下证Z∩Zj=Ø，i≠j，i，j，=1，2，...，m+1。由定义显然有Z∩Zm+1=Ø，对任意的 i=1，2，...，m 都成立。

对于 i，j=1，2，...，m 的情况，用反证法证明。假设 Z∩Zj≠Ø，i≠j，i，j，=1，2，...，m+1。则至少存在一个x∈U，使得x∈Z∩Zj

这与 {Y1，Y2，...，Ym} 是 U 的划分矛盾。所以，{Z1，Z2，...，Zm+1}为 U 上一个划分并且此时划分与其对应关系之间是一一对应的。故此，可以说通过这种划分，能够明确与之对应的唯一一个等价关系。在优化多变量测试时，将会应用到相对泛化的概念。

（三）多变量网络簇的自适应优化算法

在此算法中，定义的信息系统S是一个4元组 S＝〈U，A，V，f〉。式中 U 表示域，A 表示全部的特征集合，那么能够分为条件特征C以及决策特征表示 P 的值域；f：U×A→V，定义为信息对应的函数。从上而下的网络簇算法是根据某种标准量进行划分，最终完成测试的有效选择。然后，根据选择的测试结果完成对训练集的高效划分，使得每一个测试结果都能产生对应的分支。此算法可以应用于在选择测试中派生出的每一个类中，添加进的所有实例全部隶属于相同类，那么称为此类别为叶节点。

对于多个变量的测试过程来说，可以根据定义来进行相关描述：①运算对应的决策特征集C和D的核；②利用ID3的方法来进行最优特征值的选择，以此来作为测试的节点；③假设令P=a1∧a2∧...∧ak，运算 P 相对于 D 的泛化 GEND(P)，把它当做测试的节点。

二、实验与分析

（一）多变量网络簇异动匹配实验

0-1多变量网络簇时变问题可以描述为：当前有多变量网络簇时，多变量网络簇时变的载重量是定值，而且没有重量和价值两个属性，如果不超出载重前提是可以增加多变量网络簇时变物件的总价值。定义的0到1的多变量网络簇时变问题，就是说这些若干物件是否可以使用是不确定的，而且某些物件的价值会根据时间的变化而变化，多变量网络簇时变的载重容积也会变化，就会出现交叉情况。对第三种情况进行的研究也就是载重容积变化的情况，主要是对100个物件的0-1多变量网络簇时变问题进行了研究。如果载重的容积在不断变化的时候那么多变量网络簇时变就会震动，多变量网络簇时变的容积反映了阻尼的振动情况。

本文定义本次实验程度是120，匹配的最大极限值为120，此种模式下全部可以迭代250次。在迭代过程中，每间隔50次将会更新一次模板，执行异或计算，在场景完成5次阻尼波动以后，可以设置CR模块的比例为1。图1提供了两个CR值为0.1和0.5模块的检索值。

从图1可以看出，在场景发生变化时需要进行搜索，通常情况下将不会发生停滞警报，并且改变期限可以检索到了凹凸周围。相比较而言，SGA与PDGA的场景发生改变的时候是处于停滞的，检索能力大幅下降，尤其是SGA，根据场景的改变也随之进行变化。主要是由于SGA的检索能力因不同场景而发生改变，并且PDGA的检索能力好于SGA，在场景发生改变的情况下效率大幅下降能够将新一轮的检测得到最优解。

值得注意的是以上3种模型发生变化的时候一直没有执行初始化问题，跟目前许多移动模型的操作流程是不一样的，此问题正是本文研究的重点。模型发生改变需要重新开启，在新的模型基础上进行求解，即开展新的优化问题。每一种模型一共迭代了254次，共出现5个期限，这种曲线的长度能够达到54，但是相对普通的检索情景而言，SGA和PDGA都无法发挥出检索能力，但可以在限定的时间内计算出最大极值。并且从图1可以得出，整个期限一直处于上升趋势，经过迭代若干次后可以得到最优解。

（二）多变量网络簇时变实验

3种模型在运行的时候会间隔50代，而且多变量网络簇时变的容积也会变化。下面是对三种模型不同的振动情况下的检索能力进行比较。图2的曲线是原来的效率值通过有效率值得到的。我们可以得出，如果多变量网络簇时变的阵容及阻尼震荡的时候，DCESTM检索能力高于SGA和PDGA。虽然PKGA在50代前减速的值要好于DCESTM，但是通过图 1（b）我们得知，DCESTM 在这一期限结束的时候，检索的值高于PKGA。从图1了解到在阻尼振动的时间内是一种积极的检索过程，获得了比较连续的检索结果，在50代节奏中得到了最优解。SGA获得了阻尼振动以后检索期限是一种停滞状态而且不能够进行有效的检索，PKG在场景振动之后得到了检索而且获得了比较良好的解。从图2知道它的特色，在长期变化的时候可以积极检索，而且在新场景下可以获得最优解。

图1 异动匹配实验

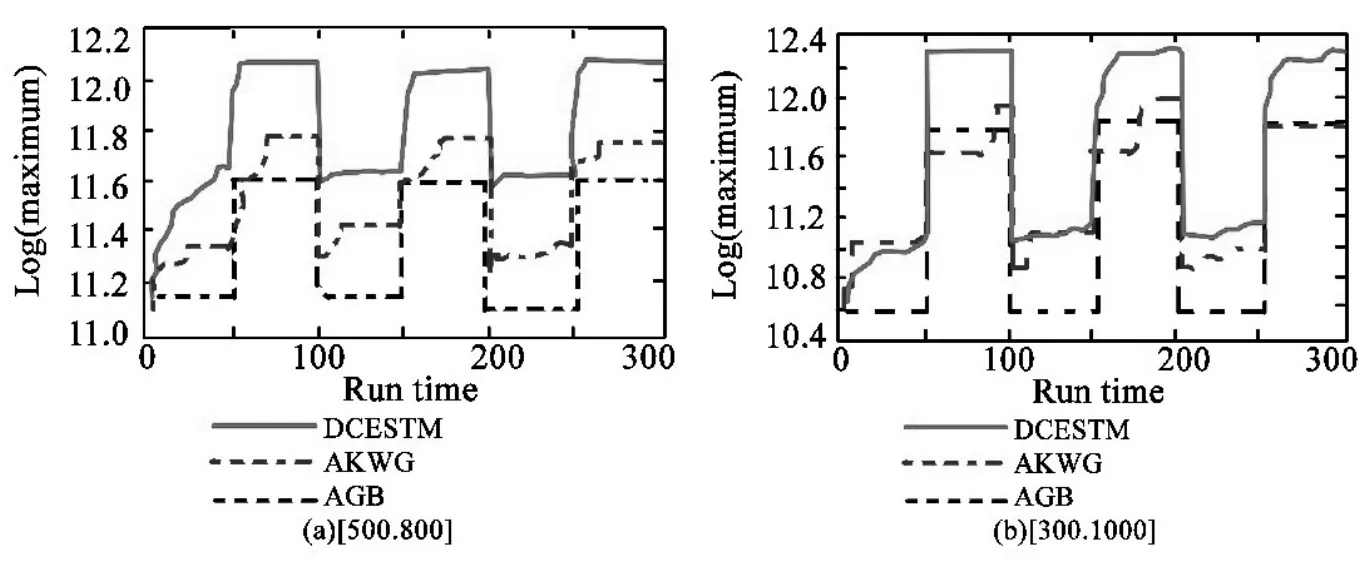
图2 多变量网络簇时变实验

需要指出的是上面的三种模型在产生变化的时候并没有开展初始化的问题，也就是说模型没有重启，和当前许多的移动模型的做法不一样。这是研究的主要目标，也就是模型在运行的时候如何准确地感受场景的变化而且依据场景的运动轨迹。改变以后模型需要重启，在新的场景基础上需要求解，这也就是一种新的优化问题。一方面不能重复使用有用信息而且不能使用外部场景知识，会导致计算时间浪费；另一方面比较而言它的检索能力更差，而且和文章的设置期限长度有密切的联系。每种模型迭代了254，出现了5个期限，曲线的长度达到了54，对于一般的检索环境来说，SGA和PDGA的检索能力无法发挥出来。但是它却能在规定的时间内获得最大的极值，而且从图1我们知道效率是在整个期限在不断上升的，迭代几次就会获得最优解。这表明模仿策略有利于和场景进行交互，并且可以获得更好的解，和单纯的检索以及消极适应比较来说有更大优点。

三、结论

本文提出了一种基于偏微分方程自适应优化多变量网络簇的方法。该方法在偏微分方程理论的基础上，完成对多变量的有效测试。其中，针对决策特征集核怎样完成高效选择问题进行了深入分析。在进行多变量测试时，通过利用另一个等价关系对优化问题进行泛化界定，根据界定的概念，可以确保多变量的检测不再局限于单纯的连接特征，而是其衍生。

参考文献：

[1]Rutkowski L,Pietruczuk L,Duda P,et al.Decision trees for mining data streams based on the McDiarmid's bound[J].IEEE Transactions on Knowledge and Data Engineering,2013（6）：1272-1279.

[2]Norouzi M,Collins M,Johnson M A,et al.Efficient non-greedy optimization of decision trees[C]//Advances in Neural Information Processing Systems.2015:1729-1737.

[3]Shahrian E V,Yousefi S,Isfahani A M,et al.Vessels segmentation in color retinal images using ensemble of bagged decision trees and patched based principle component analysis and linear discriminant analysis[J].Investigative Ophthalmology&Visual Science,2015（7）：5262-5262.

[4]Tweedie D,Polli J W,Berglund E G,et al.Transporter Studies in Drug Development:Experience to Date and Follow‐Up on Decision Trees From the International Transporter Consortium[J].Clinical Pharmacology&Therapeutics,2013（1）：113-125.

[5]Lin C F,Yeh Y,Hung Y H,et al.Data mining for providing a personalized learning path in creativity:An application of decision trees[J].Computers&Education,2013（4）：199-210.