变体飞行器有限时间收敛LPV鲁棒控制

刘正华, 温 暖, 祝令谱

(北京航空航天大学自动化科学与电气工程学院, 北京 100191)

0 引 言

常规飞行器虽然可以进行大包线、多任务的飞行,但其在不同飞行条件下的气动性能不是最优的,其气动外形是基于各个任务段的折衷设计。然而,变体飞行器依靠自身配备的智能驱动机构,可以大尺度的改变气动外形。此种技术使得飞行器能够在差异较大的飞行环境中完成拟定的飞行任务,且总体飞行性能不会出现明显的削弱。因此在航空领域中,智能变体飞行器一直作为研究热点,得到了国内外学者的广泛关注[1]。

但是变体自由度对气动参数的求取和变体动态过程中的建模与姿态稳定控制提出了更高的要求。如何建立能够真实反映变体飞行器动态特性的数学模型,同时使设计出的控制器能够保证机体变形过程的稳定性和动态响应成为了变体飞行器研究的重点之一。线性变参数(linear parameter varying, LPV)技术可以涵盖大范围的参考点并且还可以描述复杂系统由于某些参数变化而具有的动态特性[2]。因此,近年来针对变体飞行器的LPV建模和基于LPV系统的动态输出稳定控制器设计已较为成熟。文献[3]采用准定常假设气动参数的方法,给出了一种翼展可伸缩的变体飞行器纵平面LPV模型,并依赖于单一李雅普诺夫函数方法,设计了状态反馈控制器,并给出了保证系统渐进稳定的LMI条件。文献[4]对于一种后掠角可变的飞行器,设计了平滑切换LPV控制器,保证了变体过程中的切换稳定性。在文献[5]中,基于增益整定的H∞控制方法,对一种折叠翼飞行器设计了LPV鲁棒控制器。文献[6]采用基于奇异值分解的张量积转换方法,对一种大尺度的变体飞行器设计了LPV控制器。

对于原始的非线性系统,可以在多个平衡参考点上进行Jacobian线性化从而得到一系列的线性时不变(linear time-invariant, LTI)模型。之后,全局的LPV模型可以通过插值和拟合这些LTI系统而得到。这是当今最常用的飞行器LPV模型获取方法[2]。然而这种近似线性化方法无疑会带来模型参数上的不确定性。在控制器设计阶段,必须考虑由于系统参数摄动带来的模型不确定性。因此,LPV系统的鲁棒控制器是使被控对象满足理想性能的一种有效解决途径。滑模变结构技术作为一种鲁棒控制策略,由于其滑动模态的不变性使其对系统的参数摄动和外部扰动均不敏感,从而广泛的应用到不确定的LTI系统中[7-9]。但是对于LPV系统,只有少量的关于滑模技术的研究。其中大部分还是作为滑模观测器应用到LPV系统中[10-11]。在仅有的对于LPV系统的滑模控制器中,文献[12]提出了一种时变的超平面滑模控制。文献[13]设计了一种积分滑模控制器,并将其应用到实际的LPV系统模型中。在最近的文献[14]中,二阶滑模控制技术被应用到不确定的LPV系统中。但上述滑模LPV控制器都不能够有效解决系统中的不匹配不确定性问题。

故本文以一类翼展可伸缩飞行器的多胞体LPV模型为研究对象,将原先应用于LTI系统中的滑模控制技术拓展到了不确定的LPV系统中。给出了针对系统中存在的不匹配不确定性的滑动模态存在性条件和有限时间收敛的趋近律控制器设计步骤。本文的主要贡献在于:在变结构控制器的滑模面函数求取过程中,推导出一种可以很大程度降低保守性的线性矩阵不等式(linear matrix inequality, LMI)条件;通过参数依赖的Lyapunov函数稳定性分析,证明所设计的趋近律可以使系统在有限时间内收敛至滑动模态。

1 多胞体LPV变体飞行器模型

本文以左右机翼可以对称的沿翼展方向水平伸缩的轻型飞机Navion L-17[3]作为研究平台。其机翼的大幅度伸展可以迅速地影响到飞机的固有气动参数。假设可达到的最大翼展是原本体翼展的2倍,变体效果如图1所示。翼展变形率ξ=Δb/b作为变体调度量,其中Δb为翼展变形量,b为本体翼展,可知ξ∈[0,1]。

图1 变体形态示意图Fig.1 Morphing configuration

1.1 变体非线性模型描述

此变体飞行器的纵平面运动学与动力学方程是建立在飞行器的气流坐标系中。

(1)

式中,飞行空速和海拔用V与h表示;俯仰角速度和俯仰角以q和θ表示;m和Iy分别表示变体飞行器的固有质量和绕y轴的转动惯量;推力以T=Tδtδt表示,其中δt为油门开度,Tδt为油门推力系数;g代表重力加速度。

式(1)中的气动力和气动力矩以及各气动系数与迎角α、升降舵偏角δe关系的表达式均取自于文献[3]。

1.2 多胞体LPV建模

本文只考虑变体飞行器在纵向平面运动,选取飞行器的工作参考点为飞行海拔h0=1 524 m,空速V0的马赫数为0.1。且飞行器在水平无侧滑匀速平飞时进行变体运动,并以此为所研究的运动过程。对于变体飞行器的非线性系统(1), Jacobian线性化是获得其LPV模型的最常用方法。平衡点选取为ξ=0,0.1,0.2,…,1,此变体飞行器的多项式参数依赖LPV模型可表示为

(2)

对于此多项式参数依赖的LPV系统(2),采用文献[15]中的高阶奇异值分解(high order sigular value decomposition,HOSVD)方法获得其多胞体LPV模型。在综合建模准确度与计算复杂性基础上,舍弃较小的奇异值及其对应的特征向量,最终获得具有两个顶点的多胞体LPV系统如下:

(3)

式中,顶点Ai和权值函数λi(ξ)的具体表达式如下:

当基于Jacobian线性化和张量积转换,将非线性系统(1)转换至多胞体LPV系统(3)后,这两个系统模型应具有近似一致的动态响应。假设翼展变形率ξ在10 s内由ξ=0变为ξ=1,此两种模型在变体过程中的动态响应比较如图2所示。

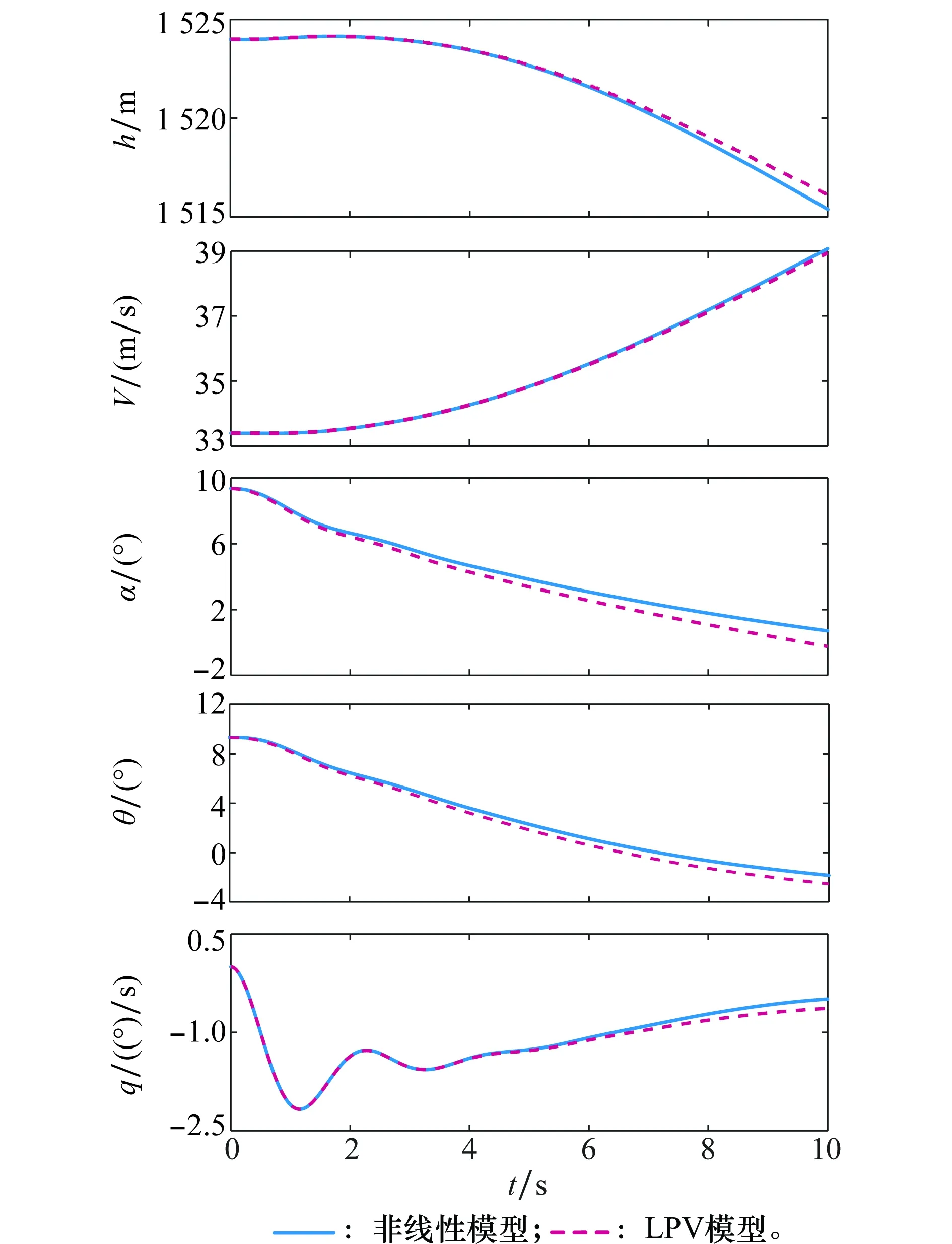
图2 LPV模型与非线性模型的开环动态响Fig.2 Nonlinear model vs. LPV model

从图2可以看出多胞体LPV模型与非线性模型的开环动态响应差别很小。多胞体LPV模型在一定程度上可以描述原始非线性系统的动态特征。因此,后续的控制器设计可以基于此LPV系统。并且由图2可得在没有控制器保证的变体过程中,高度与速度变化剧烈,不能维持原来的初始值。由于翼展变长,翼面积变大,导致升力系数变大,故攻角减小以寻求新的平衡状态。

通常情况下变体飞行器的气动参数获取是基于准定常气动假设的[15]。但是在此大尺度变体过程中气动参数会出现“滞回环”效应[16],即非定常的气动参数会出现在变体过程中,已知的气动参数存在不确定性。与此同时,整机的重心和转动惯量均会随着变体机构的运转而发生变化。故本文考虑如下的带有参数摄动项的不确定多胞体LPV系统

(4)

式中,ΔA为系统参数矩阵的摄动不确定项；ΔB为控制输入矩阵的摄动不确定项。

对于此变体飞行器带有不确定项的LPV模型,需设计鲁棒控制器使得飞行器在变体动态过程中全局稳定且变体前后保持速度与高度不变。

2 滑模鲁棒LPV控制器设计

对于不确定LPV系统(4),本文对如式(5)所表示的多胞体LPV系统设计滑模鲁棒控制器。

(5)

式中,x为系统状态变量;u为系统的控制输入;A(Θ)为系统的名义LPV系数矩阵;ΔA(Θ)代表系数矩阵参数的模型不确定量;B为系统的控制输入常矩阵;此LPV系统的时变参数向量Θ(t)=[θ1(t),…,θm(t)]T∈Rm。

假设3B为列满秩矩阵,且B⊥为矩阵BT的零空间上的任意一组基。

注1当B矩阵为时变参数矩阵或者含有不确定性时,可在控制输入量u前加入适当的滤波器使控制矩阵B(Θ)或者B+ΔB成为系数矩阵的A(Θ)的一部分[17]。故对于一般的LPV系统,通过此方法构成的增广形式的系统模型仍具备式(5)形式。

针对具有不匹配的不确定性的LPV系统(5),鲁棒滑模控制器的设计步骤主要包括:滑动模态的存在性证明和趋近律控制器设计。

2.1 基于LMI的滑动模态的存在性证明

首先,滑模面选取为

s(t)=BTP-1x(t)

(6)

式中,BT为式(5)中的控制矩阵B的转置；P为待设计的正定实对称Lyapunov矩阵。

定义转换矩阵M和转换后的状态向量v为

(7)

式中,B⊥为矩阵BT的零空间上的任意一组基。

则原系统(5)的等价转换形式为

(8)

式中,M1与M2如式(7)所示。

对于此等价形式的动态系统(8),其处于滑模面上的降阶动态[7-8]可以表示为

(9)

定理1对于给定的不确定性常数εΔ,滑模面s(t)存在且滑模切换面上的动态系统(9)是鲁棒稳定的充分条件为存在S个矩阵Pi>0,标量σ>0及分块矩阵

满足LMI约束条件式(10)和式(11):

(10)

(11)

(12)

证明根据鲁棒稳定性定理,系统(9)稳定的充分条件为存在矩阵Xc>0满足

{M1[A(Θ)+ΔA(Θ)]PB⊥}TXc+

Xc{M1[A(Θ)+ΔA(Θ)]PB⊥}<0

(13)

Π(Θ)=

(14)

为了降低由单一Lyapunov函数带来的保守性问题,本文在不同的顶点处采用不同的Lyapunov的函数,从而实现参数依赖的思想。即令P满足

(15)

则Π(Θ)可以等价的表示为

Π(Θ)=

(16)

由式(16)可知

(17)

由式(11)与式(17)可得

(18)

证毕

注2对于整个多胞体LPV系统,定理1采用文献[18]中的方法,在增加一定的计算量的前提下,没有要求存在任何公共的矩阵变量满足所需要的矩阵不等式。这与文献[19]中通过引入附加矩阵解除Lyapunov矩阵与系统矩阵耦合乘积项,从而实现参数依赖稳定思想的处理方法的根本区别。故定理1具有较低的保守性。

2.2 有限时间收敛的趋近律控制器设计

在上一节基础上,将基于参数依赖思想设计滑模趋近控制律,使不确定性LPV系统(5)在此控制律下能够在有限时间内收敛到滑模切换面s(t)=0上,并且在之后一直保持此滑动模态运动。

定理2假定滑模面式(6)存在,即不等式(10)与式(11)对于Pi有解,则不确定的LPV系统轨迹式(5)在滑模趋近律式(19)控制下可以在有限时间内到达切换面s(t)=0。

u(t)=-M2(Θ)[A(Θ)+P′(Θ)P(Θ)-1[BM2(Θ)-I]]x(t)-

κ(Θ)sign(M2(Θ)x(t))

(19)

式中,M2(Θ)如式(7)所示(并取P=P(Θ)),且

(20)

μ>0为可调增益参数。

证明选取s(t)=0作为滑模切换面,故参数依赖的Lyapunov函数选取为

(21)

(22)

此外注意到

与κ(Θ)>0

(23)

得到不等式

(24)

代入式(20),不等式(24)可以等价地表示为

(25)

证毕

3 仿真与分析

表1 参数不确定性

表2 控制器参数

对闭环系统进行50次蒙特卡罗仿真,每次仿真中各参数的不确定性独立随机变化,仿真结果如图3和图4所示。

图3 控制输出图Fig.3 Output of the controller

图4 控制效果图Fig.4 Effectiveness of the controller

由图3和图4可以看出,在变形过程中,所设计的滑模控制器在参数摄动的情况下能够保证高度只有0.2 m的变化,速度有不大于0.02 m/s的变化。且在10 s后变体运动结束时,飞行器的飞行海拔和空速与变体前相同,这是由于状态变量中存在有飞行海拔与空速的误差积分环节。由于存在参数摄动,升降舵和俯仰角速度在初始阶段会出现较大的变化,但其均在可接受的范围内。变体结束后的攻角、升降舵偏角和油门均达到新的平衡值。翼展的增加会使油门呈减小趋势,这也说明了变体飞行器依靠气动外形改变来优化飞行性能的特性。综上,所设计的滑模鲁棒LPV控制器能较好的保证变体动态过程的闭环系统性能,消除参数不确定性所带来的影响,维持变体前后定速定高飞行。

4 结 论

(1) 利用Jacobian线性化和模型张量积转换,将变体过程中非线性模型转化为多胞体LPV模型。所得的LPV模型中参数矩阵存在不匹配的不确定性。

(2) 将原先只存在于LTI系统的滑模控制器推广到此不确定的LPV系统中。此控制器设计过程分为了两步:首先给出了LMI形式的定理,保证在不匹配不确定性的情况下的滑动模态的存在性和稳定性。再者设计参数依赖的趋近律控制器,其可以使原LPV系统在有限时间内收敛至滑模切换面上。

(3) 50次非线性仿真结果表明,运用所设计的鲁棒滑模控制器,在存在参数摄动和模型不匹配的情况下,可以保证变体过程中全局稳定性,并使变体前后速度和高度不变。

参考文献：

[1] BARBARINO S, BILGEN O, AJAJ R M, et al. A review of morphing aircraft[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(9): 823-877.

[2] MARCOS A, BALAS G J. Development of linear-parameter-varying models for aircraft[J].Journal of Guidance Control and Dynamics, 2004, 27(2): 218-228.

[3] 殷明,陆宇平,何真. 变体飞行器LPV建模与鲁棒增益调度控制[J].南京航空航天大学学报, 2013, 45(2): 202-208.

YIN M, LU Y P, HE Z. LPV modeling and robust gain scheduling control of morphing aircraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(2): 202-208.

[4] JIANG W, DONG C, WANG Q. A systematic method of smooth switching LPV controllers design for a morphing aircraft[J]. Chinese Journal of Aeronautics, 2015, 28(6): 1640-1649.

[5] YUE T, WANG L, AI J. Gain self-scheduled H-infinity control for morphing aircraft in the wing transition process based on an LPV model[J]. Chinese Journal of Aeronautics, 2013, 26(4): 909-917.

[6] HE Z, YIN M, LU Y. Tensor product model-based control of morphing aircraft in transition process[J]. Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering, 2016, 230(2): 378-391.

[7] CHOI H H. Variable structure control of dynamical systems with mismatched norm-bounded uncertainties: an LMI approach[J]. International Journal of Control, 2001,74(13): 1324-1334.

[8] JUANG J C, LEE C M. Design of sliding mode controllers with bounded L-2 gain performance: an LMI approach[J]. International Journal of Control, 2005, 78(9): 647-661.

[9] HU X, WU L, HU C, et al. Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2012, 349(2SI): 559-577.

[10] ALWI H, EDWARDS C, MARCOS A. Fault reconstruction using a LPV sliding mode observer for a class of LPV systems[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2012, 349(2SI): 510-530.

[11] EFIMOV D, FRIDMAN L, RAISSI T, et al. Interval estimation for LPV systems applying high order sliding mode techniques[J]. Automatica, 2012, 48(9): 2365-2371.

[12] SIVRIOGLU S, NONAMI K. Sliding mode control with time-varying hyperplane for AMB systems[J].IEEE/ASME Trans.on Mechatronics, 1998, 3(1): 51-59.

[13] ALWI H, EDWARDS C, STROOSMA O, et al. Real-time implementation of an ism fault-tolerant control scheme for LPV plants[J].IEEE Trans.on Industrial Electronics, 2015, 62(6): 3896-3905.

[14] TANELLI M, STRADA S C, CORNO M, et al. Sliding mode control for LPV systems[C]∥Proc.of the American Control Conference,2016: 3686-3691.

[15] 孙斌,杨凌宇,张晶. 基于高阶奇异值分解的LPV鲁棒控制器设计[J].北京航空航天大学学报, 2016, 42(7): 1536-1542.

SUN B, YANG L Y, ZHANG J. Robust LPV control design based on HOSVD[J]. Journal of Beijing University of Aeronautics & Astronautics, 2016, 42(7): 1536-1542.

[16] 于勇,韩晓辉,胡俊. 变展长战术导弹非定常气动特性研究[J].飞行力学, 2017, 35(2):49-53.

YU Y, HAN X H, HU J.A numerical study on unsteady aerodynamic characteristics of Supersonic tactical missile with variable-span wings[J].Flight Dynamics, 2017, 35(2):49-53.

[17] APKARIAN P, GAHINET P, BECKER G. Self-scheduledH∞control of linear parameter-varying systems: a design example[J]. Automatica, 1995, 31(9):1251-1261.

[18] 高会军.基于参数依赖Lyapunov函数的不确定动态系统的分析与综合[D].哈尔滨:哈尔滨工业大学,2005.

GAO H J. Analysis and synthesis of uncertain dynamic systems based on parameter dependent Lyapunov function[D]. Harbin：Harbin Institute of Technology, 2005.

[19] SHAKED U. Improved LMI representations for the analysis and the design of continuous-time systems with polytopic type uncertainty[J].IEEE Trans.on Automatic Control, 2001, 46(4): 652-656.

[20] WEI X, GUO H F Z L.Composite disturbance-observer-based control and terminal sliding mode control for uncertain structural systems[J].International Journal of Systems Science,2009,40(10): 1009-1017.