双基地MIMO雷达多目标高精度跟踪算法
张正言, 张剑云
(国防科技大学电子对抗学院, 安徽 合肥 230037)
0 引 言
阵列雷达通过综合利用空间和时间信息处理技术提高了估计性能,多输入多输出(multiple-input multiple-output,MIMO)雷达进一步发展了这种技术,取得了更大的优势,属于新的雷达体制[1]。与传统的相控阵雷达不同之处在于MIMO雷达各个发射天线的信号是正交的,而相控阵雷达则是相关的,因此MIMO雷达拥有空间分集,波形分集等优势,等效于拥有更多的阵元,能够探测更多的目标[2-5]。MIMO雷达按照阵元之间的距离可以分为统计MIMO雷达与相干MIMO雷达,相干MIMO雷达无需实现时间同步,因此工程上比统计MIMO雷达更容易实现,引起了众多学者的关注。相干MIMO雷达根据收发基地是否分置划分为单基地MIMO雷达和双基地MIMO雷达,其中双基地MIMO雷达具有双基雷达与MIMO雷达的优点,作为本文研究的对象。现有的MIMO雷达方面的文献大部分都是定位方面的[6-9],而跟踪方面的研究处于起始阶段,且多数跟踪算法性能较差,特别是低信噪比时算法性能急剧下降甚至失效。
文献[10]将旋转不变子空间(estimation of signal parameters via rotational invariance techniques,ESPRIT)算法应用到双基地MIMO雷达目标参数估计中,复杂度较低,但是由于没有充分利用接收信息,估计性能有所下降,且需要额外的收发角度配对算法。文献[11]介绍了多目标分类(multiple signal classification, MUSIC)算法在双基地MIMO雷达中的应用,该算法属于空间谱超分辨算法范畴,角度估计精度较高,收发角度自动配对,不需要额外配对算法。但是付出的代价是需要波峰搜索,算法的计算量较高。
目前关于目标定位的算法大都是基于子空间类的,需要进行协方差矩阵的估计与分解,计算量较大,不能直接用于解决目标跟踪问题。
文献[12]为了解决单基地MIMO雷达目标角度跟踪问题,提出基于改进平行因子(parallel factor, PARAFAC)分析角度跟踪算法。文献[13]为了解决单基地MIMO雷达角度关联问题,利用Kalman滤波思想,并采用紧缩投影近似子空间跟踪(projection approximation subspace tracking deflation, PASTd)算法实现角度跟踪。然而文献[12-13]的计算量都较大,影响跟踪速度。因此,文献[14]利用协方差矩阵差与角度差之间的关系,得到适合单基地MIMO雷达的低复杂度跟踪算法,但跟踪性能较低。
双基地MIMO雷达与单基地MIMO雷达相比具有收发基地分置带来的优势,同时由于收发角度不同出现了新的问题。
文献[15]参考文献[14]的思想,将其扩展到双基地MIMO雷达中,通过两个近似关系,得到了相邻时刻协方差矩阵差与角度差的线性关系。该算法有效地降低了跟踪计算量,无需额外的关联算法,但是算法性能较低。文献[16]利用PASTd算法完成了双基地MIMO雷达跟踪过程,跟踪性能优于文献[15],但无法实现角度的自动关联。为了解决文献[16]的不足,文献[17] 提出基于自适应非对称联合对角化(adaptive asymmetric joint diagonalization, AAJD)跟踪算法。AAJD算法增加了滤波的思想,从收发导向矢量求取目标角度时,利用了上一时刻估计出的角度信息,将其代入收发导向矢量公式,作为下一时刻的初始矢量。算法中有滤波的思想,能够实现角度的自动关联,弥补了文献[16]的不足,但低信噪比时存在信号子空间扩展问题,造成性能的下降。
本文分析了低信噪比时AAJD算法性能下降的原因,针对信号子空间扩展问题给出相应的改进,得到与特征值作用相同的变量,对特征值进行排序,选择大特征值对应的特征矢量,得到正确的信号子空间,解决了低信噪比时算法失效的问题。因排序后特征矢量顺序是随机的,无法使用AAJD中ESPRIT算法求解角度,本文采用估计性能更高的MUSIC算法代替ESPRIT算法,并根据跟踪状态的不同将MUSIC算法分为相应的两步,减小了算法的计算量,满足跟踪要求。本文算法能够解决信号子空间扩展问题,并且对MUSIC算法进行改进,在提高精度的同时减小了算法计算量。
1 信号模型
图1为本文MIMO雷达阵列结构,M和N分别为发射和接收阵元数。所有的阵元都是均匀线性分布的,发射和接收阵元之间的间距分别用dt和dr表示。目标距离收发基地较远,可以看成远场点目标,各发射阵元发射相互正交的信号,并且有相同的带宽和中心频率。假设运动产生的多普勒频率不影响编码波形的正交性,信号的载波频率记为fc。
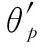

图1 MIMO雷达运动目标的示意图Fig.1 A schematic diagram of a moving target for MIMO radar
第m个阵元的发射信号记为sm(m=1,2,…,M),sm(t)为基带信号,发射信号经P个目标反射后到达接收阵列可表示为
(1)
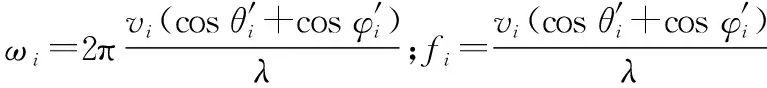
x(t)=At(φ)⊙Ar(θ)vec(diag(ε))+n(t)=
W(φ,θ)ε+n(t)
(2)
式中,W(φ,θ)=[at(φt,1)⊗ar(θt,1),at(φt,2)⊗ar(θt,2),…,at(φt,P)⊗ar(θt,P)]为MN×P维的收发方向矢量;ε=[ε1exp(jω1t),…,εPexp(jωPt)]T;⊙和⊗分别代表Khatri-Rao积和Kronecker积。假设不同的目标多普勒频移各不相同。
2 基于改进MUSIC的双基地MIMO雷达高精度角度跟踪算法
2.1 AAJD算法描述
本节对AAJD角度跟踪算法进行概述。AAJD算法通过求解函数最小值得到收发导向矢量,求解过程分为两个步骤。
(3)
式中,y(t)=x(t);d=ε。
步骤1无限制条件寻优
(4)
求导得
(5)

(6)
(7)
当相邻角度变化较小时
(8)
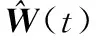
(9)
(10)
具体求解过程为
apr(θ(t))=apr(θ(t))/‖apr(θ(t))‖,
apt(φ(t))=apt(φ(t))/‖apt(φ(t))‖
(11)
由式(11)可得收发导向矢量,利用ESPRIT算法,估计出目标p的DOD和DOA。(·)T,(·)H,(·)-1分表表示转置,共轭转置,求逆操作。
最后通过得到的收发角度,更新t时刻的特征矢量,即
W(t)=At(φ(t))⊙Ar(θ(t))
(12)
2.2 低信噪比时的改进AAJD算法
随着信噪比的下降,AAJD算法求出的导向矢量精度下降,信号子空间扩展到了噪声子空间中,AAJD算法求出的收发导向矢量包含了噪声信息,前P级收发导向矢量不能正确的表示目标真实方向矢量,出现了噪声子空间与信号子空间相互交叠的情况。大特征值对应的特征矢量张成的子空间为信号子空间,因此本文对AAJD算法进行改进,从中得到与特征值作用相同的变量,用于表征信号特征值的变化,解决低信噪比时角度跟踪问题。
改进AAJD算法对AAJD算法步骤一进行改进,利用了降维的思想,基础的理论是主成分的顺序估计[18-19]。具体过程可以描述为用p=1的AAJD算法更新最大特征矢量(最大特征值对应的导向矢量),然后用接收数据向其投影并移除,获得新的数据矢量。由于最大特征矢量已经被移除,此时第二大特征矢量成为最大特征矢量,重复上述过程,P次操作后,就获得了所有的导向矢量。表1给出了改进AAJD算法步骤一的流程。

表1 改进AAJD算法步骤1的流程
在求解导向矢量的过程中,能够得到特征矢量对应的特征值,并且一次循环只得到一个特征矢量,所以特征值与特征矢量之间是一一对应的,下面给出严格的数学证明。
首先,给出一个命题,并进行相应的证明。
命题1在双基地MIMO雷达目标角度跟踪中,g(t)是改进AAJD算法中的特征值变量,λ(t)是协方差矩阵C(t)分解得到的特征值,当算法收敛时,g(t)与λ(t)作用相同,都为估计出的特征值。
证明λ(t)和W(t)是数据协方差矩阵C(t)分解得到的特征值和对应的特征矢量,根据特征值分解理论
C(t)W(t)=λ(t)W(t)
(13)
在改进AAJD算法中
(14)
将式(8)代入式(14),可得
(15)

(16)
进一步化简得
C(t)Wi(t)=gi(t)Wi(t)
(17)
将式(13)与式(17)对比可得出结论:g(t)与λ(t)相同,都为特征矢量对应的特征值,至此命题1得证。
证毕
当信噪比较低时,通过AAJD算法求出导向矢量,其张成的子空间与真实的信号子空间存在较大的误差,AAJD算法估计出的导向矢量不是真实的方向矢量。
从定理1可知g(t)与λ(t)作用相同,是判断信号子空间与噪声子空间的依据。表2给出定位静止目标时不同信噪比条件下改进AAJD算法的g(t)与λ(t)的对比。进一步说明了命题1的正确性及低信噪比时存在信号子空间扩展问题。设收发阵元数分别为4和3。

表2 不同信噪比下改进AAJD算法g,特征值λ的比较
从表2可以看出,信噪比为0时,改进AAJD 算法求出的g和特征值λ分布相同,大特征值集中在前3级,与目标个数相同。当SNR=-5 dB时,λ的值仍然集中在前3级,而g的前3个值不都是最大值,即此时对应的特征矢量存在误差,从g的分布可以看出,大特征值已经扩散到第4级。当SNR=-10 dB时,扩散问题更加严重,已经扩散到11级。根据特征值与特征矢量之间的关系,大特征值对应着目标的导向矢量,又g和λ的作用相同,因此用g作为判断依据,从中找出最大的P个值,其对应的矢量即为特征矢量。
2.3 基于改进MUSIC角度估计算法
改进AAJD算法是通过对特征值排序找出真实信号子空间的,找到的目标导向矢量是随机的,AAJD算法步骤2中ESPRIT算法不再适用,本文采用性能更高的MUSIC算法代替ESPRIT算法,并改进MUSIC算法,降低计算量。
在阵列信号处理中,大特征值与小特征值对应的特征矢量分别张成信号子空间Us与噪声子空间Un,两个空间相互正交,可知方向矢量W(φ,θ)也正交于噪声子空间
WH(φ,θ)Un=0
(18)
由于在信号处理中噪声是不可避免的,因此W(φ,θ)与Un不完全正交,为一极小值,其倒数较大,所以MUSIC算法的谱估计公式为
(19)
对式(19)进行谱峰搜索,找出极大值对应的坐标即为目标的收发角度,得到了目标的位置。
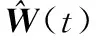
(20)
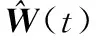
(21)
将式(21)代入式(20)得
(22)
通过改进AAJD算法,求出了目标的收发联合导向矢量,可以结合MUSIC算法求出目标的收发角度,但是MUSIC算法需要进行波峰搜索,特别是在双基地MIMO雷达中,涉及到二维搜索,计算量较大,因此对MUSIC算法进行改进。
跟踪过程可以分为两种状态:一是非收敛状态,当雷达刚捕捉到目标时,或者观察的目标个数及状态发生突变时,跟踪处于非稳定状态,目标角度的跟踪结果误差较大,而且同时要完成空域扫描任务;二是跟踪处于收敛的稳定状态,当跟踪目标一段时间后,进行了数据的积累,目标角度跟踪误差较小,可以看成是有效跟踪。
针对跟踪过程的两种状态,将MUSIC算法分为对应的两个过程。当跟踪过程处于非收敛状态时,此时雷达有两个任务,一是要对全空域进行观察,二是使跟踪进入到第二阶段即稳定跟踪状态。因此,这一阶段的MUSIC算法需要对全空域进行扫描,由于此时不是稳定状态,收发导向矢量与真实方向矢量之间的误差较大,无需进行精确扫描,可以设置较大的步长进行粗扫描,求出目标在空域中的大致位置,为下一阶段的跟踪过程做准备。
跟踪的第二阶段为稳定状态,此时目标个数及状态不会发生突变,跟踪结果与目标实际位置误差较小,属于有效估计。当进行t时刻目标角度估计时,t-1时刻的估计角度可以看成是先验信息,因为目标个数及状态不会发生突变,因此可以预估t时刻目标所处的大致区域,并且AAJD算法的前提条件是相邻时刻之间的角度变化较小,可以在t-1时刻估计出的目标角度(φ,θ)上,预测t时刻目标角度位于([φ-a,φ+b],[θ-c,θ+d])范围内。a、b、c和d为常数,根据目标运动速度确定大小,a、b、c和d越小,算法需要的计算量越小,但是目标角度误差有增大的风险。为了进一步减小稳定状态时MUSIC算法的计算量,本文假设目标的收发角度不会同时相等,因此可知([φ-a,φ+b],[θ-c,θ+d])范围内只有一个目标,MUSIC算法是通过搜索比较找出峰值点,估计出目标角度,所需的计算量较大。而已知([φ-a,φ+b],[θ-c,θ+d])范围内仅有一个目标,因此无需找出峰值点,仅需找出最大值即可,其对应的角度为目标角度,将二维搜索比较过程变为求最大值过程,减小了算法的计算量。
下面给出改进MUSIC算法的过程:
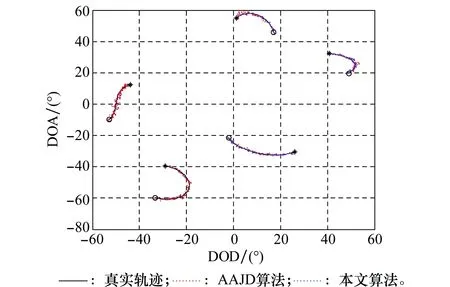
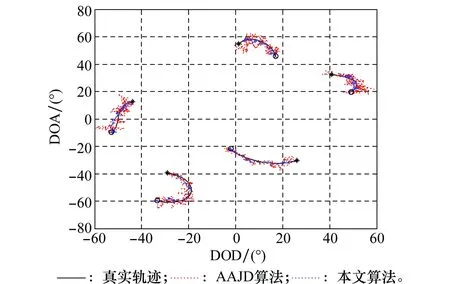
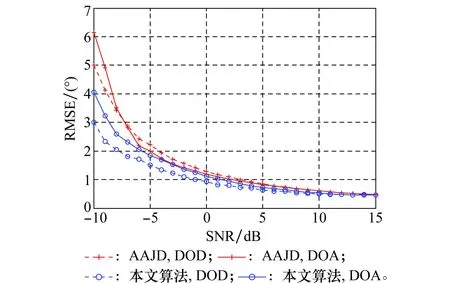
Ift 此时跟踪处于非稳定状态,需进行全空域的大步长粗搜索: 搜索范围ω=([-90°,90°],[-90°,90°]); 搜索步长设为1°。 利用式(19)~式(22)找出峰值点,并从中选择值最大的P个峰值点对应的坐标即为目标角度。 Else 此时跟踪处于稳定状态,需进行固定小空域的小步长精细搜索: 搜索范围:ωt,i=([φt-1,i-a,φt-1,i+b],[θt-1,i-c,θt-1,i+d]) 搜索步长设为e。 利用式(19)~式(22)找出区域中的最大值,对应的坐标即为目标角度。 End 其中,φt-1,iθt-1,i为t-1时刻估计出的目标发射角和接收角。K,a,b,c,d,e都为常数,K表示目标是否处于稳态,a,b,c,d根据目标运动速度确定,搜索步长e由跟踪精度要求确定。 步骤1根据经验设置跟踪收敛门限K; 步骤3如果i≤K时,结合2.3节改进MUSIC算法,求出目标的角度,跳转到步骤2; 步骤4如果i>K时,结合上一时刻估计出的角度,预测出目标角度的取值范围ωt,i=([φt-1,i-a,φt-1,i+b],[θt-1,i-c,θt-1,i+d]),结合第2.3节改进MUSIC算法,求出目标角度跳转到步骤5; 步骤5将估计出的目标角度代入收发联合导向矢量公式得到W(t),并作为下一时刻的初始矢量,跳转到步骤2。 不难看出本文算法具有如下的优点: (1) 为了解决低信噪比时AAJD算法失效的问题,改进AAJD算法求出与特征值作用相同的变量,求出更加精确的噪声子空间,解决了低信噪比AAJD算法失效的问题。且改进AAJD与AAJD算法求解特征矢量时的计算复杂度为O(MNP+P)和O(MNP+P2),当待估目标数较多时,改进AAJD算法能大大减小计算量。 (2) 改进AAJD算法采用估计精度更高的MUSIC算法代替ESPRIT算法,提高了双基地MIMO雷达目标角度跟踪性能。 (3) 改进AAJD算法对MUSIC算法进行改进,根据跟踪状态,将MUSIC算法分为相应的两种过程:非稳定状态全空域的粗搜索和稳定状态小范围的精细搜索,降低了算法的复杂度。为了满足跟踪要求,进一步降低计算量,将稳定状态的峰值搜索变为取最大值操作。 值得注意的是,虽然本文算法中的MUSIC算法会增大计算量,但是通过改进降低了增加的计算量。 假设双基地MIMO雷达的收发阵元间距均为波长的一半,发射哈达码波形脉冲信号,保证各个阵元的发射信号相互正交。阵元发射的载波频率为1 GHz,发射脉冲宽度为10 μs,脉冲重复频率为10 kHz,目标散射系数dp和加性噪声都是随机产生的。 实验1定位静止目标 假设存在4个点目标,收发角度为(θ1,φ1)=(30°,-40°),(θ2,φ2)=(40°,20°),(θ3,φ3)=(-50°,-20°)和(θ4,φ4)=(-16°,35°)。收发阵元数M=N=4,观测脉冲K=150,遗忘因子β=0.95。给出不同信噪比下本文算法与AAJD算法的仿真结果。为了进行有效对比,只给出稳定状态的跟踪结果,根据经验取K>50以后的数据进行对比。信噪比SNR=10 dB时仿真结果如图2所示,信噪比SNR=0 dB时仿真结果如图3所示,信噪比SNR=-5 dB时仿真结果如图4所示。 从图2可以看出,本文算法与AAJD算法估计结果都与目标真实角度相互重合,这说明本文算法与AAJD跟踪算法都能够成功定位目标。这是因为在信噪比较高时,噪声影响较小,本文算法与AAJD算法估计出的导向矢量中不包含噪声成分,信号子空间不存在扩展现象,与真实的方向矢量相同,能够从中估计出目标的真实角度。从目标星座图可以看出本文算法估计精度高于AAJD算法,这是因为本文算法采用了估计精度更高的MUSIC算法。 从图3仿真结果中可以看出本文算法与AAJD算法都有效,估计出了目标的真实位置,但是AAJD算法在部分快拍数时失效,稳定性低于本文算法,这是因为AAJD算法在信噪比SNR=0 dB时,部分快拍估计出的收发导向矢量与真实方向矢量误差较大,受到了噪声的影响,其中包含了噪声的矢量,因此估计出了错误的目标角度。本文算法性能优势进一步扩大,这是因为解决了低信噪比时信号子空间扩展的问题。 图2 SNR=10 dB时两种算法的估计结果Fig.2 SNR=10 dB estimation results of two algorithms 图3 SNR=0 dB时两种算法的估计结果Fig.3 SNR=0 dB estimation results of two algorithms 图4 SNR=-5 dB时两种算法的估计结果Fig.4 SNR=-5 dB estimation results of two algorithm 从图4可以看出,本文算法能够实现目标角度估计,而AAJD算法估计出了错误的角度,这是因为在信噪比较低时本文算法通过对特征值进行排序,估计出更加准确的收发导向矢量,解决了信号子空间的扩展问题,在信噪比较低时仍然能够成功定位目标。 对比图2~图4,可以看出本文算法性能都优于AAJD算法。高信噪比时本文算法使用MUSIC算法代替ESPRIT算法,提高了跟踪定位精度。随着信噪比的下降,AAJD算法性能急剧下降直至失效,而本文算法仍然有效,说明本文算法的有效性及理论分析的正确性。 实验2多个运动目标跟踪结果的验证 空中观测区域内存在5个运动目标,均为远场点目标,双基地MIMO雷达的收发阵元数M=N=4,发射脉冲个数K=500,遗忘因子β=0.85。信噪比SNR=5 dB本文算法与AAJD算法仿真结果如图5所示,信噪比SNR=-5 dB仿真结果如图6所示。 图5 SNR=5 dB两种算法目标跟踪结果Fig.5 SNR=5 dB target Angle tracking of two algrithms 图6 SNR=-5 dB两种算法目标跟踪结果Fig.6 SNR=-5 dB target angle tracking of two algrithms 在图5中,两种算法的跟踪结果都与真实轨迹重合,说明两种算法都成功跟踪到了运动目标。从图6中表明本文算法的跟踪结果仍然较好,而AAJD算法误差较大,说明AAJD算法已经失效,而本文算法仍然能够成功跟踪目标,这是因为本文算法找到更加准确的信号子空间。对比图5和图6的跟踪结果可以发现本文估计轨迹与真实轨迹重合度高于AAJD算法的重合度,说明本文算法跟踪性能高于AAJD算法。 实验3算法的性能随SNR的关系 本文算法的性能优势的验证。将本文算法与AAJD算法的RMSE进行比较。对空中4个目标进行跟踪,收发阵元数M=N=5,信噪比SNR=-10~15 dB,观测脉冲数K=400,蒙特卡罗仿真次数M=500,取100≤K≤400用于求解RMSE(稳定状态),图7为实验结果。 实验结果表明本文算法的RMSE低于AAJD算法,且随着信噪比下降,本文算法与AAJD算法的RMSE都增大,但是AAJD算法上升的更快,两者之间的RMSE差增大,信噪比较低时AAJD算法已经失效。这是因为在信噪比较高时,本文算法中的MUSIC算法性能优于AAJD算法中的ESPRIT算法,低信噪比时,本文算法得到正确的噪声子空间,估计出的目标角度更加准确。 图7 RMSE随SNR的变化Fig.7 Change of RMSE along with SNR 基于AAJD算法的双基地MIMO雷达目标跟踪性能较低,特别是低信噪比时算法性能急剧下降甚至失效。本文对AAJD算法进行改进,找出与特征值相同作用的变量,按特征值变量大小对特征矢量进行排序,找出更接近真实方向矢量的收发导向矢量,得到的噪声子空间更加准确,解决低信噪比时AAJD算法无法跟踪目标的问题。并且引入MUSIC算法,提高了跟踪性能,对MUSIC算法进行改进,将其分为更适应跟踪的两个过程,有效地减小了计算量。 参考文献: [1] FISHER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radar-models and detection performance[J]. IEEE Trans.on Signal Processing, 2006, 54(3):823-838. [2] 王珽, 赵拥军. 基于三迭代与二阶锥规划的机载MIMO雷达稳健降维STAP方法[J]. 航空学报, 2015, 36(11):3706-3714. WANG T, ZHAO Y J. Robust reduced-dimension STAP method for airborne MIMO radar based on TRIA and SOCP[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(11):3706-3714. [3] 王伟, 王咸鹏, 马跃华. 基于多级维纳滤波的双基地MIMO雷达多目标定位方法[J]. 航空学报, 2012, 33(7):1281-1288. WANG W, WANG X P, MA Y H. Multi-target localization based on multi-stage Wiener filter for bistatic MIMO radar[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7):1281-1288. [4] ZHANG Y, ZHANG G, WANG X H. Computationally efficient DOA estimation for monostatic MIMO radar based on covariance matrix reconstruction[J]. Electronics Letters, 2017,53(2):111-113. [5] 梁浩, 崔琛, 余剑. 基于ESPRIT算法的十字型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1):80-89. LIANG H, CUI C, YU J. Reduced-dimensional DOA estimation based on ESPRIT algorithm in monostatic MIMO radar with cross array[J].Journal of Electronics & Information Technology, 2016, 38(1):80-89. [6] ZHENG G M. DOA Estimation in MIMO radar with non-perfectly orthogonal waveforms[J]. DOA estimation in MIMO radar with non-perfectly orthogonal waveforms[J]. IEEE Communications Letters, 2017, 21(2):414-417. [7] WANG X P, WANG L Y, LI X M, et al. An efficient sparse representation algorithm for DOA estimation in MIMO radar system[C]∥Proc.of the 17th IEEE Access International Workshop on Signal Processing Advance in Wireless Communication, 2016:1-4. [8] KHOMCHUK P, STAINVAS I, BILIK I. Pedestrian motion direction estimation estimation using simulated automation MIMO radar[J]. IEEE Trans.on Aerospace and Electronic Systems, 2016, 52(3):1132-1145. [9] SHI J P, HU G P, ZONG B F, et al. DOA estimation using multipath echo power for MIMO radar in low-grazing angle[J]. IEEE Sensors Journal, 2016, 16(15):6087-6094. [10] LI J F, JIANG D F, ZHANG X F. DOA estimation based on combined unitary ESPRIT for coprime MIMO radar[J]. IEEE Communications Letters, 2017, 21(1):96-99. [11] TAN J, NIE Z P, WEN D B. Low complexity MUSIC-based direction-of-arrival for monostatic MIMO radar[J]. Electronics Letters, 2017, 53(4):275-277. [12] WU H L, ZHANG X F. DOA tracking in monostatic MIMO radar using PARAFAC-RLST algorithm[C]∥Proc.of the 3rd International Conference on Information Science and Engineering, 2011:958-961. [13] ZHANG X F, LI J F, FENG G P, et al. Kalman-PASTd based DOA tracking algorithm for monostatic MIMO radar[C]∥Proc.of the International Conference on Information, Services and Management Engineering, 2011:220-224. [14] YU H X, ZHANG X F, CHEN X Q, et al. Computationally efficient DOA tracking algorithm in monostatic MIMO radar with automatic association[J]. International Journal of Antennas and Propagation, 2014(12): 1-10. [15] 张正言, 李小波, 徐旭宇, 等. 双基地MIMO雷达角度快速跟踪算法[J].信号处理, 2016,32(6):701-706. ZHANG Z Y, LI X B, XU X Y, et al. Target angle rapid algorithm for bistatic MIMO radar[J]. Signal Processing, 2016,32(6): 701-706. [16] WU L H, ZHANG F X. DOD and DOA tracking for bistatic MIMO radar using PASTd without additional angles pairing[C]∥Proc.of the 5th IEEE International Conference on Advanced Computational Intelligence, 2012: 1132-1136 [17] ZHANG W T, LOU S T, LI X J, et al. Tracking multiple target in MIMO radar via adaptive asymmetric joint diagonalization[J]. IEEE Trans.on Signal Processing, 2016, 64(11): 2880-2893. [18] YANG J, KAVEH M. Adaptive eigensubspace algorithms for direction or frequency estimation and tracking[J]. Signal Processing, 1988, 36(2): 241-251. [19] BANNOUR S, AZIMI-SADJADI M R. An adaptive approach for optimal data reduction using recursive least squares learning method[C]∥Proc.of the IEEE International Conference on Acoustics, Speech, and Signal Processing, 1992: 297-300. [20] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京:清华大学出版社,2004:27-28. WANG Y L, CHEN H, PENG Y N, et al. Theory and algorithm of spatial spectrum estimation[M]. Beijing:Tsinghua University Press,2004: 27-28.2.4 算法流程
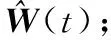
2.5 算法的性能分析
3 仿真实验




4 结束语

