面向高风电渗透系统调频需求储能UP的开发

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.国网辽宁省电力有限公司计量中心，辽宁 沈阳 110000；3.吉林松江河水力发电有限责任公司，吉林 白山 134504)

1 引言

大力开发利用风能是实现能源可持续供应的重要选择，风电联网是实现风能大规模开发利用的有效途径，世界各国都将风电开发作为能源发展战略的重要部分。我国风电装机已跃居世界第一，装机容量逾一亿千瓦，规划到2020年，装机容量将达到2亿千瓦。

我国风电主要分布于缺乏灵活功率调节能力的三北电网，大规模风电功率波动给电力系统功率调节造成了严峻挑战。

风电机组采用最大功率点跟踪(Maximum Power Point Tracking，MPPT)控制策略时，机组不响应电网频率变化。随着风电渗透率的增加，电网总惯性降低，电网抗功率扰动能力减弱，高风电渗透电网的调频问题将显得越来越突出。

储能系统被认为是提高电网风电接纳能力的有效手段。随着储能技术的不断进步，大规模储能成本将不断下降。近期Lux Research的一份研究表明，车载电池组价格已经下降了35%，并在未来十年其成本仍将大幅度降低。因此，储能系统在电力系统中的应用将更加广泛。

PSASP(Power System Analysis Software Package)是国内应用最为广泛的电力系统仿真计算软件，所提供的用户自定义程序接口(UPI)，使用户能够根据研究需要自由建模，增强了PSASP仿真功能。

目前，在UPI环境中进行储能调频仿真研究鲜有文献报道。针对储能系统参与高比例风电电力系统调频率问题，研究了储能系统参与电力系统调频控制策略，研发了相应的PSASP-UPI模型，基于WSCC-9系统，仿真分析了储能参与电网调频性能，对所提出的控制策略及研发的UPI模型的有效性进行了验证。

2 储能系统参与电网调频控制策略设计

储能装置以其快速调节功率、控制策略易于实现等特点，在缓解高比例风电接入后电力系统的频率问题的应用愈显关键。

2.1 UPI环境下储能频率应用数学模型

系统频率波动是电力系统中供需能量不平衡导致能量形式改变的表现。当能量出现盈余时，由于电力系统需要保持能量供需的实时平衡，因此剩余的能量就需要转化为系统内发电机转子的动能，体现为系统频率升高。因此，储能模型可以选择直接控制频率偏差或者通过平抑风功率波动来进行频率调节。

本文所建立的储能调频模型是以平抑风功率波动为目标，具体数学模型如下：

目标函数：

MinΔP=∑PG+PW+PStorage-PL

(1)

约束条件：

PStorage=VT·IT·cosθ

(2)

X=F(X,Y,U)

(3)

Y=G(X,Y,U)

(4)

Xi.min≤Xi≤Xi.max

(5)

Yi.min≤Yi≤Yi.max

(6)

Ui.min≤Ui≤Ui.max

(7)

其中：

ΔP—系统内有功功率的偏差量;

PG—系统内发电机组的有功出力;

PW—系统内风电机组总有功出力;

PStorage—系统内总负荷消耗的有功功率;

PL—系统内总负荷消耗的有功功率;

VT—储能装置接入点节点电压幅值;

IT—储能装置注入到系统内的电流幅值;

θ—储能装置接入点节点电压相角。

在PSASP暂态稳定计算中，外部注入功率需要以注入电流形式表达，因此，模型中将储能系统的输出用式(2)表示；其中的节点电压矢量需要在PSASP暂态稳定计算结束后获取，故模型中式(3)及式(4)表示暂态稳定计算中的线性网络方程组及动态微分方程组，式(5)至式(7)是暂态稳定计算状态量及控制变量取值范围的约束。

目标函数中Pstorage所对应的VT和θ为式(3)和式(4)中进行暂态稳定计算中解得状态量中的部分量；式(3)和式(4)中的控制变量U为式(2)中由注入功率所转化得到的节点注入电流IT，因此，按照储能UP开发逻辑将上述模型整理得：

UP：

(8)

PSASP/ST：

(9)

模型中较为复杂的求解微分方程由PSASP自带的程序进行运算，这极大的减少了用户UP程序的开发量，同时PSASP中自带的求解方法也保证了计算的收敛性。

2.2 UPI环境下储能UP的开发

本文实现储能参与系统调频功能共需要编写3个UP程序，分别实现潮流初始计算、读入风电功率波动数据、储能系统动作三项功能。其中潮流初始计算是稳态潮流UP，其余两项为暂态稳定UP，因此接口的设定规则略有不同。

对于潮流初始计算UP(UP.dll)，其功能是以风电波动初始时刻的功率为输入量，计算得到初始的稳态潮流分布，作为后续暂稳计算的基础。UP的描述信息中，由于UP并不需要从PSASP内取得变量，因此输入信息，即UP.F1为空。而UP需要将风功率初始值输入到PSASP主程序中，使其进行潮流计算，因此UP.F2风电功率P。PSASP的调用信息中，所设定的风功率注入母线为发电3母线，UP名称及编号与程序内所设一致即可。

对于储能动作UP(Storage.dll)，其功能是按设定的储能控制策略进行充放电操作，注入到风电场所在母线。如2.1储能模型中所分析的，PSASP暂稳计算主程序反馈量只能是有功电流及无功电流，因此需要计算出能与储能输出功率等效的有功、无功电流。出于对此的考虑，UP需要从主程序中取得功率注入母线电压幅值及相角，以计算电流，故UP.F1为VT和θ。UP向PSASP主程序反馈量为等效储能出力的有功电流及无功电流，因此UP.F2为注入电流IT生成有功分量ITR和无功分量ITI。PSASP的调用信息中，所设定的风功率注入母线为发电3母线，UP名称及编号与程序内所设一致即可。

对于风功率读入UP(Read.dll)，与储能动作UP(Storage.dll)同为暂态稳定用户自定义程序，因此其F1、F2设置选择相同，且两者的根本目的均为向网络注入功率，故此UP的F1与F2设置量与前述一致。

2.3 储能控制策略的制定

2.3.1 储能控制策略制定思路

风电功率波动量是衡量风电并网的重要考核指标之一，采用储能系统平滑风电功率波动也是当前常用的手段[9-11]。本文储能UP所采用的是以风电输出功率平均值为动作参考值，以平抑风电功率波动为目标的控制策略。其中考虑蓄电池荷电量、储能系统充放电功率、储能充放电效率以及储能系统容量。

2.3.2 储能控制策略的制定

由于电化学形式的储能装置，具有能量密度高、安装布局灵活、维护较为方便、技术成熟等优点。因此当前已投运的储能示范工程中所用的储能形式多为电化学储能。

受电化学电池工作原理影响，蓄电池并不适宜多次数的深度充放电。研究表明，当电池荷电状态SOC处于10%到90%之间时，电池的适用性良好，而电池长时间工作在上限及下限10%SOC区间内，将导致电池电化学反应物浓度降低，甚至增加电极材料和电解液的性能衰退[12]。因此，在控制策略中首先对储能装置当前荷电状态SOC进行判定，若SOC处在10%到90%区间，则允许储能装置动作。

在高风电渗透电网中大规模加入储能装置，根本上是为了提高系统实现能量实时平衡的能力。因此，需根据储能装置的最大充放电功率以及储能装置最大容量，判定当前储能系统是否能完全平抑风电功率波动，再据此修正储能系统实际应充放的电量。

综上所述，具体储能控制策略如下：

(1) 判定当前电池荷电状态SOC；

表1 电池荷电状态SOC判定表

(2) 若SOC处在10%到90%区间，以风电输出功率平均值Pavr为标准，衡量系统有功功率偏差ΔP的正负来判定当前装置需要充电还是放电；

(3) 比较储能系统充放电速率及充放电容量限额与平抑当前波动量所需速率及容量大小，确定储能充放电量。

其中：

(10)

ΔP=Pwind.i-Pavr

(11)

当ΔP>0，即储能装置需要充电时，控制策略如表2。

表2 储能系统充电过程控制策略

其中：PS.C为储能系统最大充电功率，SN为储能系统额定容量。

SS.C=(0.9-SOC)·SN

(12)

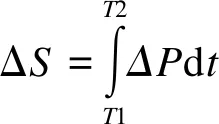
(13)

ΔP1=ΔP

(14)

ΔP2=PS.C

(15)

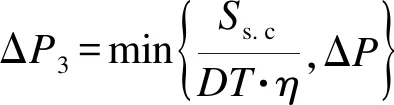
(16)

(17)

当ΔP<0，即储能装置需要放电时，控制策略如表5所示。

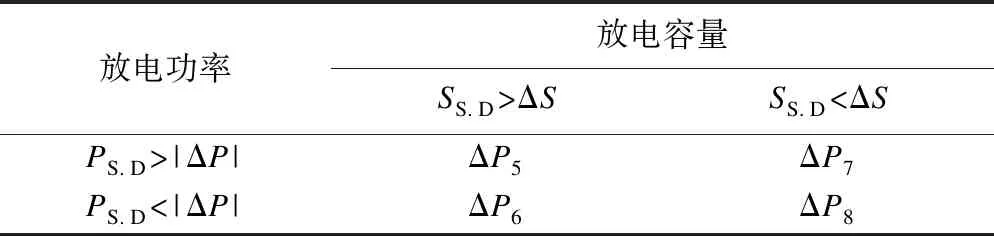
表3 储能系统放电过程控制策略

其中：PS.D为储能系统最大放电功率。

ΔP5=|ΔP|

(18)

ΔP6=PS.D

(19)

(20)

(21)

3 UPI环境下用户程序UP的应用原理

3.1 PSASP/UPI基本工作原理

PSASP提供用户程序接口(UPI)环境，用户可按照需求开发UP程序，使PSASP功能模块和用户程序模块联合运行，共同完成某一计算任务[13]。

在Windows操作系统中，可以借助其所提供的动态链接库(DLL)支持，以实现计算机语言与逻辑控制的交互。用户所编写的UP是基于事先按照接口规约设置的控制数组(F1和F2)，完成UP程序与PSASP主程序之间的信息传递。在使用UPI功能时，需将已编译好的UP程序生成所需的DLL文件，再进入PSASP界面中设定与F1和F2相对应的UPI接口参数，以实现PSASP对UP的调用，进而与程序联合迭代。

3.2 用户程序UP和PSASP主程序的接口原理

3.2.1 用户程序与潮流程序的接口原理

常规潮流潮流计算(LP)的数学模型为非线性代数方程组：

F(X)=0

(22)

其中：X=(x1,x2,…,xn)为网络方程求解的状态变量；

在潮流计算中，针对非线性代数方程组一般均采用牛顿拉夫逊法、P-Q分解法等迭代法进行求解，迭代格式如下：

X(K+1)=G(X(K))

(23)

当考虑用户程序，式(1)所示的非线性方程组改为[15]：

F(X,U)=0

(24)

用户自定的UP数学模型表示为式4：

H(X,U)=0

(25)

其中：U=(u1,u2…,um)为用户程序方程求解所得的控制变量。

上述PSASP中的潮流计算(LF)方程式(24)与用户程序方程式(25)之间相互交替运算，在求解潮流方程式(24)时将控制变量U看作固定值，解得系统状态变量X，选取X中UP需求量X*，作为PSASP的输出信息F1数组，输入到UP中；在求解用户程序式(25)时将状态变量X看作固定值，解得UP所得到控制变量U，选取U中潮流计算程序需求量U*，作为UP的输出信息F2数组，输入到潮流计算主程序中，两者交互，直至LF和UP其中一只计算完成为止。两者之间具体的交互关系如图2所示，其中t表示LP和UP交替运算的次数。

3.2.2 用户程序与暂稳计算程序的接口原理

暂态稳定计算(ST)的数学模型其中包括描述网络结构的线性方程组、表征系统动态与案件及自动设备的微分方程组，因此，暂态稳定计算可归结为线性网络方程及微分方程的联立求解：

图1 LP&UP交互关系

(26)

若考虑用户自定义程序方程，则将式修改为：

X=F(X,Y,U)

(27)

Y=G(X,Y,U)

(28)

U=H(X,Y,U)

(29)

暂态稳定计算ST与UP之间的交互关系与1.2.1中所述类似，式中所进行的暂态稳定计算是由PSASP所带程序包独立完成，在考虑用户自定义程序UP时，先将式(27)及式(28)中控制变量U当做常数，解得状态变量X、Y，再将UP所需要的部分状态量X*、Y*作为F1数组输入给UP方程式(29)，解得控制变量U，将ST所需部分控制变量U*作为F2数组反馈给ST，进而完成迭代过程，直至结束。PSASP的暂态稳定计算(ST)中，微分方程组按分步积分进行求解，积分步长DT可自行设定， ST与UP每一时段均交替计算一次，具体交互关系如图2。

图2 ST&UP交互关系

4 仿真算例及分析

为了验证前文所提出的运用储能系统参与高风电渗透系统调频可行有效，本文以标准WSCC-9三机九节点系统为基础，将其中母线3所接火电机组改为风电机组，构造算例系统。

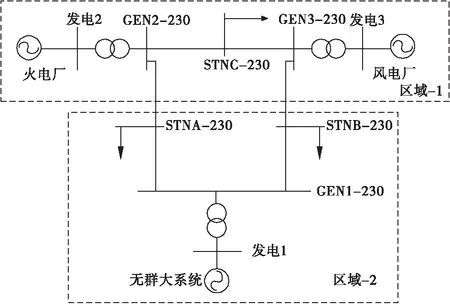
图3 算例系统单线图

算例系统总负荷315MW，基准容量100MW，网络图中发电母线一为平衡节点，发电母线二接火电机组，实际出力为163MW，风电机组额定出力为85MW，风电出力占比为27%。

4.1 风电功率波动情况

风电大规模接入电网对电力系统一次调频能力影响最大[12]。因此，算例中主要在一次调频时间尺度下进行分析，仿真时间长度选择为30s。设定风电波动场景，风电输出功率波动如图4所示。

图4 风电输出功率曲线

其中，风电功率基准值为100WM，最大输出功率标幺值为0.48，最小输出功率标幺值为0.34，最大变化率为10WM/s。

4.2 系统频率随风电功率波动变化情况

算例中，随风电功率波动，与潮流初始值相比就产生正向或负向偏差，随即出现了加速及减速功率，使系统频率发生波动。将4.1中所示的风电功率加到算例系统中，所得系统频率波动情况如图5所示。

图5 系统频率随风电功率波动变化曲线

由仿真结果可知，当系统受到图3所示的风电扰动时，系统最大频率偏差为0.228Hz，超过电力系统正常运行对系统频率偏差要求的±0.2Hz。

4.3 储能装置参与系统频率调节

本算例通过PSASP软件进行仿真，开发储能UP通过软件自带的UPI接口与PSASP潮流计算主程序进行交互。算例中所加的储能系统容量为5WMh，充放电最大速率为4WM，充放电效率为0.8，储能系统依照3.2中所述的控制策略进行动作。在算例系统风电功率波动不变情况下，加入储能系统后系统频率变化情况如图6所示。

图6 加入储能后系统频率变化曲线

由仿真结果可知，加入储能装置后，系统由于受到风电功率波动产生的频率偏差最大值为0.018Hz，较储能装置前，系统频率偏差显著降低，证明在电力系统内加入储能装置对于频率的改善有明显帮助。

4.4 储能装置充放电功率对频率改善影响

储能装置参与系统频率调节，根本上是实现能量在时空上的平移。实际工程中，储能系统的工作状态经常在充与放之间切换，并不会长时间处于某一状态，因此储能系统的充放电功率就对频率的调节效果产生显著影响。算例系统自身容量较小，所加的储能装置容量也有限，故只讨论储能系统充放电功率对频率调节效果的影响。

所选储能系统功率为4WM，加入后，系统频率偏差最大值减小为0.018Hz，而电力系统正常运行频率允许偏差量为0.02Hz，故已经不需要再提高储能充放电功率使系统频差降低，下面讨论功率降低时系统频率偏差的变化情况。

当储能系统充放电功率为3WM时，频率偏差情况如图7所示。

图7 加入3WM储能系统后频率变化曲线

当储能系统充放电功率为2WM时，频率偏差情况如图8所示。

图8 加入2WM储能系统后频率变化曲线

由仿真结果可知，当储能系统充放电功率降至3WM及2WM时，系统频率偏差增加到了0.025Hz及0.039Hz。故当储能容量一定时，增大的充放电功率可使系统频率偏差降低。

5 结论及展望

本文基于PSASP软件，在UPI环境下实现运用储能参与高风电渗透系统调频的功能。文中提出了一种以风电输出功率平均值为动作参考值，以平抑风电功率波动为目标的蓄电池充放电控制策略，并采用用户程序UP实现所提出的控制策略。而后在WSCC-9算例系统中进行仿真，结果证明储能系统的运用可以有效降低高风电渗透系统中频率的最大偏差量，且储能充放电功率越大、效果更好。

本文的重点在于PSASP/UPI环境下实现储能功能的开发，并未对储能系统的优化配置进行深入的分析。对于从电路系统全局考虑的储能装置的配置，还需针对储能配置地点进行研究。