高中物理学习中应用微元法进行解题的实践分析

姜凯元

(山东省青岛格兰德中学 266035)

“微元法”指的是在局部具有相同物理规律的前提下，将一个复杂的大问题分解为多个小问题，即多个“元”，然后选择其中最具有代表性的局部进行分析，从而解决整体问题.“微元法”的使用可以把变化的物理过程转变为不变的物理过程，从而简化了物理问题，是高中生必须要掌握好的物理方法之一.

一、“微元法”解决变力做功问题

将一个复杂的问题进行分割，即可以让原来问题变得简单化.在力学问题当中，常见的“元”有：“线元”、“面积元”、“质量元”以及“时间元”等.在解决实际问题时，首先需要分析研究对象，选取最为合适的“微元”，然后运用所学物理规律分析“微元”的运动过程，最后叠加求解整个过程.

例1 现使用一个大小为10N，方向沿圆周切线方向的力作用于小滚珠，让其沿着半径为R的圆周运动，请思考：当滚珠回到起点时，力F做功的大小.

解析在本题中，由于力的方向时刻在变化，不能从整个过程考虑，使用恒力做功的公式，但是力的方向始终与物体的运动方向相同.选择“线元”来解决此题，即将整个圆周分为若干个小部分，观察每个“线元”，我们可以认为是恒力做功，使用公式W=F·ΔL,所有的小部分之和为整个圆周的周长，因此可以得到W=∑F·ΔL=F∑ΔL=F·2πR=2πRF.

例2 将一木块水平放置在光滑的水平面上，左端使用弹簧与竖直墙壁链接，右端有一水平方向的力作用于木块，使物体缓慢前进，已知弹簧的劲度系数为k，求拉力对木块做的功？

二、“微元法”解决运动问题

高中物理当中诸多的运动学概念都使用了微元法进行定义，在人教版的教材上，微元法已经有所体现.例如在阐述瞬时速度时，教材考虑的时运动对象从t到t+Δt这段时间内速度的变化，将Δt趋于零即可以认为这段时间内的平均速度即为瞬时速度.实际的解题过程当中，运动的合成与分解等问题上使用到“微元法”，可以让解题效率得到显著提高.

例3 在距离水平面h高的平台上，现使用定滑轮匀速拉动水平面上的一木箱，现假设水平面与木箱之间不存在摩擦力，若人匀速拉动绳子的速度大小为v，则当绳子与水平面夹角为α时，求木箱运动的速度.

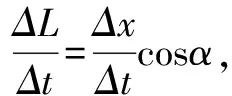
三、“微元法”解决综合性问题

上述的三个例题都是“微元法”的简单应用，但是实际的考试当中，综合类的题目仍然占很大比重.综合类的问题往往会结合力学、电磁学、运动学等各个知识点进行综合性命题，这类题目往往难度较大，对学生物理的综合能力要求较高.解决综合性问题时，首先要求学生能够熟练掌握题目中涉及到的相关物理概念以及规律，然后找到使用“微元法”的研究对象，借助数学知识，解决问题.下面结合具体的题目进行分析：

例4 有两条间距为L的平行导轨.导轨的上方有一个平行板电容器.现将导轨放置于匀强磁场当中，方向垂直于导轨所在的平面.将一个金属棒放置于导轨上，金属棒沿着导轨由静止开始下滑，且始终接触良好.现已知导轨与水平地面之间的夹角为α，电容器的电容为C，磁感应强度大小为B，金属棒质量为m，与导轨之间的动摩擦因子为μ.求：金属棒的速度大小与时间的关系.

分析此题综合性较强，考察了电学、电磁感应以及运动学等多方面的知识.拿到题目以后，首先需要对问题进行分析：在一个时间段流经金属棒的电荷量等于平行电容器极板在该时间间隔内增加的电荷量.从而建立起一个与时间相关的等式.因此此题中选择“时间元”进行解答.

经过上述例题，可以发现使用“微元法”进行解题时，思路是将一个整体的物理问题分解成为多个局部的问题，进行分析思考之后，将结论放回到整体中.关键在于找到最具代表性的“元”.常见的解题步骤：1)判定研究对象 2)分析局部的过程和规律 3)叠加到整体进行求解.

随着物理改革的不断深入，高中生面临的物理问题越来越复杂，综合性更强.对高中物理的学习造成了更多的困难.“微元法”是处理复杂物理问题常用的一种思维，教师在授课过程中，要让学生明白“微元法”思想的核心并且学会根据具体的题目进行应用.教师要把重心放在方法和技巧的教学上，让学生的综合物理素养得到提高.

参考文献：

[1]崔利花.分析高中物理解题中“微元法”的应用探析[J].数理化解题研究,2015(15):56-56.

[2]曹志扬.微元法在高中物理解题过程中的应用分析[J].中学生数理化:学习研版,2017(9):84-84.