由一道高考试题的一题多解浅谈微专题教学设计

孙宝金 李翠玲

(辽宁省朝阳市喀左蒙高中 122300)

一、问题的提出

题目已知抛物线C:y2=2x，过点(2,0)的直线l交C于A,B两点，圆M是以线段AB为直径的圆

(1)证明：坐标原点O在圆M上；(2)设圆M过点P(-4,2)，求直线l与圆M的方程.

这是2017年全国统一考试·丙卷(全国卷Ⅲ)理科数学第20题.本题直线与抛物线的位置关系、直线与方程、圆的方程，意在数形结合思想和化归与转化能力，难度适中，可以很好地考查学生的平面解析几何的基本素养.

二、问题的探究

1.基本解法的探究

笔者在审视这道高考试题时，发现可以从三个视角完美解决这道试题.

视角一：“斜率乘积为-1”

设出l的方程，通过联立方程，证明直线OA与OB的斜率之积为-1.

(1)设A(x1,y1),B(x2,y2)，l:x=my+2.

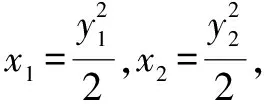
所以OA⊥OB,故坐标原点O在圆M上.

(2)略

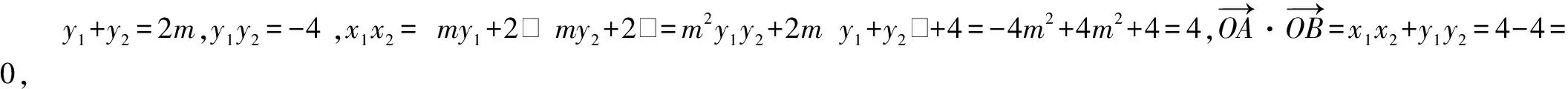
所以坐标原点O在圆M上.

(2)略

视角三：点与圆的位置关系

由已知可求圆的方程，再把O(0,0)代入满足圆的方程，即得证.

所以⊙M方程(x-m2-2)2+(y-m)2=(m2+2)2+m2.把点O(0,0)代入检验满足⊙M方程，所以坐标原点O在圆M上.(2)略

2.为了进一步让学生理解，可以对此题进行一些变式，以便学生对此类方法的理解更加深刻

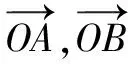
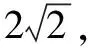
这样的“微专题”教学，培养了学生思维的广阔性，提高了学生的应变能力.关于目标意识，解题时，一要通过审体明确题目要求我们做什么，二要根据题干及结论的特点，弄清楚我们已知了什么.这样，当学生用常规思路解决问题而思维受阻时，就会尝试从结论出发或通过不同渠道去解决.

3.微专题设计及教学中教师角色

微专题设计以学生为中心，针对学生的知识漏洞设计成专题，学生在学习过程中具有更多的主动权，但这并不意味着学生可以完全离开教师的指导进行探究.事实上，在整合的过程中，教师要扮演内容呈现者、学习帮助者和课程设计者等多重角色，教师要在对学生的学习控制和学生的自主活动之间达到一种平衡状态.不断引导学生的思维，帮助学生顺利穿越“最近发展区”，获得进一步的发展，使得学生根据实际的需要寻找或构建支架支持思维能力的提高.

4.微专题具有很强的实用性、可操作性

从学生实际出发，针对学生的疑难点及解题方法的归纳，切实帮助其解决实际问题.此时教者对学情及例题难度的把握尤为重要，过难过易对学生的发展都是无益的.教师可以利用变式训练和问题引申设计来编制微专题，教学中，通过设置“典型例题——一题多解——变式训练”来完成微专题，这样可以达到“由点到面的爆炸式复习”.另外，微专题教学可以使学生，从各个不同的方面联系所学知识，形成横向、纵向的知识网.经过这样“深加工”，学生在解决问题时才能举一反三，游刃有余.

三、微专题实践反思

教学中的“微专题”复习与大专题复习不是相互对立、互不兼容的两种复习方式，二者是相互渗透，互为补充的关系.一方面“微专题”积少成多，能对大专题的自然生成起到一定的补充和完善作用；另一方面，大专题的落实需要更多有效的“微专题”进行渗透、强化.所以充分发挥微专题的问题集中、操作灵活、指向性强以及更容易解决具体问题等优势，将使得大专题复习实而不空，深而不偏.总之“微专题”复习能有效地帮助学生解决现实问题；同时教师在研究实践中不断学习、思考、分析，寻找出路，并能有所启发和创新，这对于教师自身的成长是有益的.

参考文献：

[1]李宽珍.基于目标意识解题的微专题教学——由一道模拟题谈开去[J].数学通讯,2017(4)：26-28.

[2]邱慎海.对一道全国高中数学联合竞赛题的探究[J].数学通讯，2017(4):58-61.