巧用错误提高数学学习的有效性

石新鉴

(浙江省新昌中学高一(1)班 312500)

一、利用错误 思辨概念

数学概念是反映一类事物数量关系和空间形式的本质属性的思维形式，它排除了对象具体的物质内容，抽象出内在的、本质的属性.同学在学习概念的时候，总是听起来很容易，但落实到做题目上，就会漏洞百出，对数学概念经常是顾此失彼，只知其一不知其二.

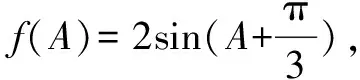
案例2 又如a⊥b是a·b=0的什么条件？很多人认为是充要条件，其充分性是显然的，其必要性是不成立的.错误的根源是向量数量积的概念，a·b=|a||b|cosθ，可见a·b=0，|a|、|b|及cosθ都可能为零，如果前提两个向量为非零向量则充要条件成立.如此看来，由于概念理解问题导致解题错误的情况比较普遍，但是我们可以利用这种普遍错误提升对概念的理解.

二、巧用错误 促进思维发展

“学始于思，思始于疑”，学习是从问题开始的，问题是思维的起点.在课堂上老师巧妙利用错误和我们一起解决错误，我们能从多角度进行分析、多方面进行改正、多方法进行解决，可以促进同学发散思维的发展.另外，在纠错的过程中，可以有效促进思维的缜密性.

案例3 设数列{an}的前n项和为Sn，首项a1=1，满足an+1=3Sn，求an.

错解an+1=3Sn，an=3Sn-1，两式做差得an+1-an=3an，则an+1=4an，数列{an}为等比数列，an=4n-1.

很多同学都很认同这个解法.于是，教师就让两组同学分别求a2.用递推公式求得a2=3，用通项公式求出a2=4，可见此题解答错误.那么，教师又问这种解答为什么是错误的呢？怎样才会正确呢？

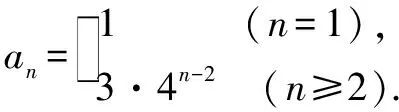
同学乙表示反对，说：“归纳猜想不一定正确，因为是不完全归纳，只有经过证明才可以.”

同学丙说：“那我们就先猜想再证明，我利用了数学归纳法进行证明了！”

教师对同学的缜密的思维进行了表扬，并表示先猜想再证明是正确的解答方法，但数学归纳法证明过程比较复杂，让同学们再次关注黑板上的错解过程.同学仔细观察了解题过程，才有所醒悟，因为an=Sn-Sn-1要求n≥2，由于忽视了n的范围，使得an+1=4an被认为是从第一项起的等比数列，于是就导致了错误.

教师总结：“数列中n的范围就相当于函数中自变量的取值范围，对于值域来说相当的重要，同学们以后要多关注一下，‘勿以n小而不为’啊！”

三、师生相助 共悟错误根源

数学课堂不是教师一个人的课堂，也不是同学的课堂，而是师生互利互助的课堂.当课堂出现错误解答时，教师不能直接讲正确的答案，而要让同学讨论错解的过程，再适当地启发同学主动探究，引导同学敢于和善于发现问题或提出问题.

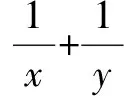
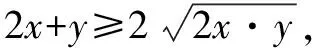
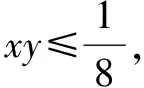
解题出现一些错误，其实都是正常的，往往这些错误是弥足珍贵的，它不仅可以反馈课堂教学存在的问题，我们同学可以用错误为新的支点，在学习中集体讨论，深入探究，最终提升学习的有效性.

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准[M].北京:人民教育出版社,2006.