关于圆锥曲线中的联列问题
周潇滔
(浙江省嵊州中学高二(16)班 312400)
一、问题引入

这看似是一道基础题,由于圆和椭圆关于x轴对称,并且总有椭圆的顶点这一个交点,所以圆方程和椭圆方程联列一下根据判别式,就可以出结果了,但事实正是如此吗?我们来实践一下.
解b2x2+a2y2=a2b2①,

将③代入①整理得:
(b2-a2)x2+a3x-a2b2=0.
Δ=a6+4a2b2(b2-a2)>0⟹(a2-2b2)2>0


3x2+4y2=12①,
(x-1)2+y2=1②.
将②代入①得:
8x-x2=12⟹x1=2,x2=6.
那么问题出在了哪里?
首先我们无法保证该圆与椭圆的值域相同,换句话说,当该圆与椭圆值域相同是显然必有三个交点,故我们只需讨论值域不同时的情况.
既然值域不同,这必定不是等价代换.

先前我们已证明方程(b2-a2)x2+a3x-a2b2=0必有根,且一根为x2=a,

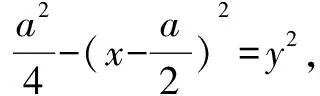

若y2<0即a2(a2-b2)2<(3ab2-a3)2
小结:所以联列方程,用方程判别式来解答并不能保证排除原方程增根的出现.也就不能用判别式来判断实根的情况了.但是若对联列后的方程进行定义域的约束,即在0 在进行二次曲线联列时我们要牢记约束条件,那么,当我们将直线与二次曲线联列时,为什么可以“忽略”约束,直接用判别式呢? 整理得(a2k2+b2)x2+2mka2x+m2a2-a2b2=0. Δ=4m2k2a4-4(a2k2+b2)(m2a2-a2b2)>0⟹b2+a2k2>m2. 那么满足这个条件的两根就一定落在定义域内吗? 我们不妨算出这两根. 如果要证明其符合定义域,只要证明-a≤x1 假设x2≤a成立, a2k2+b2>0,a2k2+2akm+m2=(ak+m)2≥0, 故假设成立,同理x1≥-a也成立 的确我们证实了x1,x2都会落在椭圆内部,也就是说只要满足判别式大于等于0,就会有实数根. 那么我们再从等价代换角度来看这个问题. ①中的y2必须满足0≤y2≤b2,而y2=(kx+m)2②中的y2却只满足了y2≥0, 所以这并非等价代换,即必须对x进行约束0≤(kx+m)2≤b2. 总结:直线与二次曲线联列并非不需要约束条件,只是在运算过程中约束会自动成立. 所以无论二次曲线和二次曲线还是直线和二次曲线联列都需要进行有效的等价代换只是一个有必要写出约束条件,另一个约束已成立了. 1.探索二次曲线联列“无需”约束情况 我们来简单地看一道题 例1 求t的取值范围使得抛物线y2=2px与抛物线x2=2p(y+t)有交点(p>0). 把③代入②得 用判别式显然不行,倒不如用导数来做方便. 记f(y)=y4-8p3y-8p3t, f(y)′=4y3-8p3. ∴24/3p4-8p421/3-8p3t≤0, 显然两条曲线相切时,y2=2px在x轴上方的曲线表示为 因为两条曲线在(x0,y0)处的切线为同一条,故其斜率相同, 可以发现相切时的t与之前算出来的最小值正好相等而且不难看出当t越来越大时曲线x2=2p(y+t)不断下移,那么必与曲线y2=2px有交点,故答案正确. 我们再回到最初代换. y2=2px中的x∈[0,+∞),x2=2p(y+t)中的x∈R. 虽然两个x值域并不相同,但y2=2px中x的取值范围是x2=2p(y+t)中x的子集. 这样的代换使被代者和代者之间为子集关系,缩小范围的代换依然成立. 2.探究直线与二次曲线联列“需要”约束的情况 直线与二次曲线联列一般无需考虑约束,但也有例外. 我们来看一下 按照常规思维,我们联列利用判别式可得出结果. 但这真的是最终答案吗? 有时简单的题目不能想当然去做,理所当然的联列使用判别式,有时也有陷阱,或许画个图进行观察可以发现一些问题. 故无论二次曲线与二次曲线,还是直线与二次曲线都需要谨慎下笔,没有什么绝对的成立与不成立,多想一下,绕过题设的陷阱,用实践去检验. 高考中两个二次曲线联列的问题也屡见不鲜,单近年来似乎为了回避这个暗区,这样的题目渐渐少了,下面我们来看一道2009年的全国卷高考题 如图,已知抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A,B,C,D四个点. (1)求r的取值范围; (2)当四边形ABCD的面积最大时,求对角线AC,BD的交点p的坐标. 当年许多考生一拿到这道题便将y2=x直接与圆(x-4)2+y2=r2,联列运用判别式来求解: y2=x①, (x-4)2+y2=r2②. 将①代入②得 看似正确的解法却又不幸掉入了出题者的陷进之中很明显考生没有抓住“等价”二字,盲目地替代导致扩大了范围.现在对原方法改进一下: 代换得:x2-7x+16-r2=0(4-r≤x≤4+r). 也就是说在x∈[4-r,4+r]范围内,必须保证x2-7x+16-r2=0有两个正解. 设f(x)=x2-7x+16-r2,则 盲目代换只会增加出现增根的可能性,遇见二次曲线的联列切忌直接使用判别式. 评析仔细观察本题在对x约束时我们还可以做文章. 上文中的4-r≤x≤r+4是对(x-4)2+y2=r2中的x进行约束,约束使得解出来的x满足在圆内,那么我们难道不能对(x-4)2+y2=r2中的y2进行约束吗? 第一种方法固然成立,而第二种方法本质是约束y2.因为y2=x, 那么方程如果有解,且这个解是符合y2∈[0,r2],那么对于(x-4)2+y2=r2来说这个解就不会是增根,因此这个约束是成立的. 参考文献: [1]徐燕.高中生对圆锥曲线的理解[D].上海:华东师范大学,2009.二、温故知新

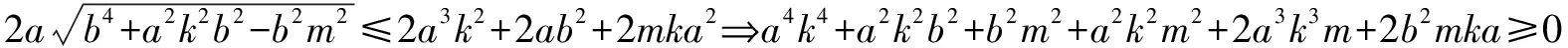
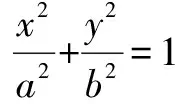
三、深入研究










四、走进高考



