一种新型压电式偏摆平台的设计与性能测试

王耿， 王帅旗

(河南理工大学 机械与动力工程学院， 河南 焦作 454003)

0 引言

偏摆平台是现代光机电系统中常见的一类重要部件，广泛应用于激光通信、自适应光学、目标跟踪、复合轴精密跟踪、原子力显微镜、激光雷达、光束稳定、激光扫描等领域[1-3]。这类系统的高效工作通常要求使用高精度的高性能偏摆平台。偏摆平台的输出运动一方面依赖于机械运动形变；另一方面依赖于其内部使用的驱动器，如音圈电机、压电致动器、微机电系统、静电驱动器等。近年来，压电式偏摆平台[4-5]由于具备响应速度快、定位分辨率高、输出驱动力大、无摩擦、真空和电磁兼容等优点，在高精度定位系统中获得了更广泛的关注。

文献[6-7]表明压电平台的跟踪定位性能主要受限于两个因素。一个因素是平台较低的固有频率限制了系统的跟踪精度和控制带宽。一方面，这个影响因素可以通过设计紧凑型结构来提高固有频率[8]；另一方面，当平台较低的固有频率无法提高时，为了得到更高的响应速度并保持较高的跟踪精度，也可以通过采用合适的控制方法[9-10]来实现。另一个因素是压电系统存在的非线性特性[11-12]，包括迟滞、蠕变和未知干扰等。此外，系统中所使用的传感器也可能会对平台性能造成影响。因此，目前开发一个高性能的压电式偏摆平台仍然是一项具有挑战性的任务。目前，许多研究机构和公司都开发了各式各样不同性能的压电偏摆平台。德国PI公司研发的S-330平台具备0.5 μrad角度分辨力、2 mrad偏摆范围、0.2 kg质量、3.7 kHz机械谐振频率。华中科技大学研发的用于激光扫描的偏摆平台尺寸为60 mm×50 mm×25 mm，具有±12 mrad偏摆范围、70 g质量、1.8 kHz 1阶谐振频率[13]。法国CEDRAT公司生产的V-DTTXS35压电平台质量为35 g，平台直径为38.1 mm，空载谐振频率为3.2 kHz,最大扫描角度范围为±2 mrad. 在有关压电偏摆平台设计的文献报道中，驱动元件和测量元件大都采用成熟的产品[14]；当采用相同的控制方法时，平台性能的差异主要源自于结构设计的不同，尤其是采用柔性结构可以获得高精度、无摩擦、无间隙、结构紧凑、高固有频率等优良特性。文献[15]基于柔顺并联机构设计了一种用于微操作领域的角度偏摆机构。文献[16]设计了一种基于柔性铰链的大行程旋转定位平台，可以实现角度和转矩自感知。

文献[13]设计的激光扫描偏摆平台需要两个压电驱动器，导致尺寸较大，增大了成本。文献[8]设计的偏摆平台谐振频率偏低，仅为180.4 Hz. 一般情况下，尺寸较小的平台易于达到结构紧凑、高谐振频率的特征。

本文据此设计和开发了一种新的基于柔性结构[17]的压电式驱动偏摆平台，包括平台机构设计与原理分析、有限元仿真分析、原型测试及PID跟踪控制实验等。该平台具有尺寸紧凑、无摩擦、高跟踪精度、高谐振频率的特点。

1 复合柔性铰链设计与分析

本节提出了一个能够实现二级放大的复合柔性铰链机构，它是基于柔性结构的紧凑型压电式偏摆平台的主要运动部件。该复合柔性铰链的工作原理如图1所示，可以看出它由下半部分的八边形框架和上半部分的柔性转动部分组合而成。图1中符号⊗表示固定连接。事实上，该柔性铰链采用电火花线切割一体化加工而成，充分利用了柔性结构的特点实现了二级放大。八边形框架基于三角放大原理实现第1级放大，柔性转动部分基于差动原理实现第2级放大。当在图1中标号1处由压电驱动器施加向上(或向下)的位移量时，会在标号2和标号3处产生水平向右(或向左)的放大输出位移量，进而推动柔性转动体在标号4和标号5处产生差动转角输出，实现偏摆动作。该复合柔性铰链采用铝合金材料7075制作而成，在其底边和转轴处固定，运动过程中不存在摩擦，进而提高了偏摆精度，而且结构紧凑、具有2 697 Hz的谐振频率。

为了计算该结构的实际偏摆量程，需要对二级放大复合柔性铰链进行分析。考虑到材料性能和几何关系，首先采用材料力学方法进行简化解析计算，然后用有限元法进行验证。该复合柔性铰链可以看作是八边形框架部分和柔性转动体的结合，二者通过两个内力对(F,F′)相联系。F和F′大小相等、方向相反，相互作用于对方。如图2所示，在框架结构上部施加一个向上的输入位移Δy，此时框架结构左右两个竖直杆的中部都会受到来自柔性转动体向左的力F′；根据力的相互作用原理，柔性转动体会受到来自框架结构向右的反作用力F. 因此，可以把该复合柔性铰链看成两个物体，由F和F′联系在一起。为了便于分析计算，假设图2中只有蓝色的部分可以产生弹性变形，其他部分视为刚体。

如图3(a)所示，当八边形框架结构施加向上的输入位移Δy时，会在A′点产生一个向右的位移量Δx，同时柔性转动体会在A′点对八边形框架结构有一个向左的拉力F′，使其产生向左的位移Δx′. 因此，在A′点的实际位移量w满足：

w=Δx-Δx′.

(1)

图3(a)中标出的L3为该八边形框架结构的左下杆m的长度。该八边形结构基于三角放大原理在输入位移Δy作用下的变形，其几何关系满足：

Δx=L3(sinα-sin(α-Δα)),

(2)

Δy=L3(cos(α-Δα)-cosα),

(3)

(4)

式中：α为倾斜杆件与竖直方向的夹角。

柔性转动体对八边形框架结构施加的向左拉力F′可以等效为一个新的力F′/2和力矩M，如图3(b)所示。根据梁在力和力矩作用下的弯曲理论，可得八边形框架结构在拉力F′作用下的水平位移Δx′为

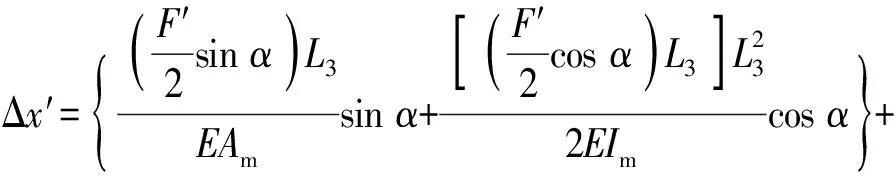
(5)

式中：Am和Im分别为杆件m的横截面积和惯性矩；E为材料的弹性模量；L2为八边形框架结构左边中部竖直杆的长度。

根据(1)式、(4)式、(5)式可得向左的拉力F′满足:

(6)

图3(c)所示的柔性转动体具有两个完全相同的转动杆，转动半径均为L4. 为表述方便，记左边的转动杆为n. 在图3(c)的A′和B′点处均作用了一个力F，它是八边形框架结构对柔性转动体的反作用力。这两个力分别等效为作用在A点和B点处的力F和力矩MF. 根据前面的假设，图3(c)中只有蓝色的部分能够产生变形，其他部分视为刚体，因此，A′点的水平位移与A点的水平位移相等。基于梁的弯曲理论，可得A′点的水平向右的位移量为

(7)

式中：An和In分别为杆件n的横截面积和惯性矩；β为左边转动杆n与竖直方向的夹角，γ为A′点到转动中心的连线与竖直方向的夹角，并且MF=FL4(cosγ-cosβ).

根据力的相互作用原理，可得内力对之间满足|F|=|F′| . 根据几何约束关系，可知柔性转动体A′水平向右的位移量与框架结构在A′的实际位移量w相等，因此有：

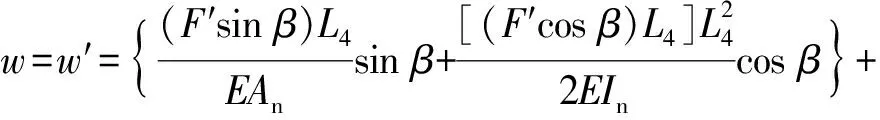
(8)

联立(6)式和(8)式，代入参数值后可得A′点的实际位移量为

w=0.124 2Δycotα.

(9)

由于该柔性转动体为左右对称结构，偏转角一正一负，实现了2倍的差分放大，因此偏摆角θ满足：

(10)

将(9)式代入(10)式可得偏摆角θ为

(11)

当输入位移Δy为5 μm时，将表1中的参数α、γ、L4值代入(11)式，可得该偏摆平台的偏摆角约为0.20 mrad.

表1 偏摆平台的部分结构参数

为了进一步验证上述解析结果的正确性，采用有限元方法对该复合放大铰链进行静力学分析。当施加5 μm的位移输入时，产生的竖直方向变形图如图4所示。从图4可以看出，转动体上部横杆左边沿处的竖直位移为4.716 μm，根据转动半径L4折合成角度值为0.22 mrad. 这个值与解析结果有0.02 mrad的误差，这个误差是由于解析计算时的刚性假设和简化分析所造成的，处于可以接受的范围内。

2 紧凑型压电式偏摆平台结构和工作原理

图5为本文所设计的紧凑型压电式偏摆平台结构示意图，主要部件包括底座、二级放大复合柔性铰链、微型应变式压电驱动器、两个侧边固定支撑、镜座、镜面等。其中，微型应变式压电驱动器[18]集驱动和位移感知功能于一体，采用过盈配合镶嵌在复合柔性铰链内部。当施加电压之后，应变式压电驱动器通过伸长或缩短来实现对偏摆平台的位移输入，其内部的应变输出信号代表了位移输出量，可通过标定对偏摆平台的输出角度实现间接测量。每个侧边固定支撑均与复合柔性铰链的转动中心轴和底座固定联接。该紧凑型压电式偏摆平台加工装配后的实物原型如图6所示，其工作过程为：微型应变式压电驱动器在输入电压信号下伸长或缩短，给偏摆平台施加一个位移输入，推动复合柔性铰链相继实现三角位移放大和差动位移放大，从而使得偏摆器能够实现偏摆动作；同时应变式压电驱动器输出的应变信号可用于监测平台的输出角度，进而实现对偏摆角的反馈控制，例如可通过设计控制器来抑制压电材料自身的迟滞非线性效应，提高其偏摆输出值的精度。

待原型制作出来之后，采用自准直仪对该压电式偏摆平台的应变输出信号进行了标定。经多次测试可知，当施加750 V电压时，驱动器的伸长量达到了最大值，由自准直仪测量得到的偏摆角为0.16 mrad，同时平台的应变输出信号为4.59 V，因此标定系数为34.9 μrad/V. 该角度范围与前述的解析值0.20 mrad和有限元分析数值0.22 mrad之间存在较大误差。除了简化的解析计算、装配误差、测量误差等因素之外，一个重要原因是在解析分析和有限元分析时，偏摆角度的计算仅仅考虑了二级放大复合柔性铰链，没有考虑其内置的应变式压电驱动器和其上端的镜座与镜面影响。为此，重新进行有限元分析，分析时加入了压电驱动器和镜座与镜面，图7中显示镜面上部右端处的竖直位移为3.560 μm, 折合成偏转角为0.169 mrad，与实验测试结果0.160 mrad存在5%的误差。这个结果是可以接受的，而且本平台的设计目标是满足高精度和高谐振频率特性，而测试得到的偏摆角度0.160 mrad已可以满足使用要求。

所设计的压电式偏摆平台具有较为紧凑的结构，尺寸为45 mm×45 mm×40 mm，质量为65 g，设计负载为可粘贴在镜座上的镜片，质量为12 g. 为了了解该平台的带载动态性能，采用扫频测试法分析了该压电式偏摆平台的带载频率特性，得到的频响曲线如图8所示。从图8可以看出，该偏转平台具有较复杂的振型和较高的谐振频率，其前3阶谐振频率约为1 610 Hz、1 999 Hz、2 525 Hz. 如果负载增大，则谐振频率降低。如果去掉负载，则平台的谐振频率将会提高。

3 实验及分析

3.1 实验平台

为了实现较为精确的定位和跟踪功能，还需要对压电式偏摆平台进行闭环控制，以确定其精度等性能。为此，在精密隔振平台上搭建了相应的实验测试系统，实验装置及其结构如图9和图10所示。一个电压信号被压电驱动高压放大器放大100倍之后，施加到压电式偏摆平台内部的应变式压电驱动器上使其产生位移动作，同时会产生一个代表角位移大小的应变输出信号。这个信号被NI-9237电桥调理模块采集后送入嵌入式实时控制器NI-cRIO-9036进行处理，经一定的算法计算后得出一个输出控制信号，通过NI-9269模拟输出模块输出到高压放大器来对压电式偏摆平台进行驱动。上位计算机用来开发和显示，并通过网线与下位机控制器进行通信。实时控制器主要用来执行控制算法，如本文中采用常规PID算法。PID控制器的3个参数通过Ziegler-Nichols法进行整定。该偏摆平台依靠材料的柔性变形实现偏转动作，偏转范围比较小。平台底座和两侧固定支撑的质量相对较大，工作时二者均处于静止状态。平台底座和隔振实验台之间固定连接，因此其中心位置不会移动，实验中也未出现中心位置移动的现象，说明了该平台性能良好。

3.2 定位与跟踪实验

首先，测试了该压电式偏摆平台的分辨力。由于标定后的应变输出信号电压值代表了平台的偏摆角度，可以用该电压信号来计算平台的角度分辨力。给该平台施加一个0 V的输入电压，会从应变模块得到其输出噪音信号。经过多次测量，得到的噪音如图11(a)所示。图11(a)中选用的测量时间为3.5 s，采样频率为10 kHz. 从图11(b)中该信号的柱状可以看出，该输出信号基本符合高斯正态分布，同时可计算出其标准差为0.49 μrad. 根据拉依达准则，选取3倍标准差作为输出信号的分辨力[19]，因此可得该偏摆平台的角度定位分辨力约为1.5 μrad. 需要说明的是，该平台的角度定位分辨力是以测量次数足够多为前提，并根据应变传感器的输出信号计算出来的。由于无法做到无穷多的测量次数，实际测量结果存在较小程度的随机性误差。而且测量时没有滤除高频噪声，该柱状图的峰顶中间出现了一定程度的凹陷，但是该结果仍然基本符合高斯正态分布。

为了测试该压电式偏摆平台的准静态定位性能，进行了一个阶梯状参考信号的阶跃跟踪实验，参考定位角的间隔是0.03 mrad. 该偏转平台在闭环PID控制模式下的角度输出响应如图12所示，从中可以看到定位比较稳定，闭环的稳态峰峰值误差约为4.2 μrad，处于稳态值的±3 μrad之间，而且随时间的延长没有出现漂移现象，蠕变带来的定位误差基本消除。这是由于闭环反馈控制作用消除了蠕变非线性的影响，该偏摆平台可用于长时间稳定定位。

为了进一步检验该偏摆平台在闭环条件下的角度跟踪性能，分别测试了在开环和闭环条件下跟踪0.5 Hz正弦曲线的实验效果。图13(a)给出了开环条件下的参考跟踪曲线、实际曲线及其误差，图13(b)给出了代表参考跟踪曲线和实际输出曲线之间关系的迟滞曲线。从图13可以看出，开环条件下跟踪误差较大，这主要是由于压电材料的迟滞非线性效应导致的。图14(a)给出了闭环条件下的参考跟踪曲线、实际输出曲线及其误差，图14(b)给出了参考曲线和实际曲线之间的迟滞曲线关系。与图13的开环跟踪效果相比，在图14的闭环PID控制条件下该偏转平台对0.5 Hz正弦曲线的跟踪性能有较大改善，误差由开环时的25.0%下降到1.4%，跟踪精度得到明显提高，参考曲线和实际曲线之间基本呈线性关系。当跟踪曲线的频率由0.5 Hz增加到1.0 Hz时，跟踪精度会有所降低。图15(a)给出了闭环条件下跟踪1.0 Hz的正弦曲线所得到的实际曲线，其跟踪误差占满行程的1.9%，比开环时的25.0%下降了23.1个百分点，跟踪精度显著提高，可以实现对1.0 Hz正弦偏转角的有效跟踪。图15(b)给出了参考曲线和实际曲线之间的迟滞关系，与图14(b)相比迟滞有所增加，但仍然比开环效果要好得多。需要说明的是，由于受压电蠕变效应的影响，在跟踪的起始时刻传感器的输出存在一定的漂移，进而导致在图14(b)和15(b)中部下方出现了一个小线段。它表示在初始时刻参考角度为0°时实际角度不为0°，但是这并不影响实际的闭环控制效果。因为闭环周期比漂移的时间尺度小得多，所以一旦开始闭环控制蠕变带来的定位误差就会基本消除。此外，采用PID算法只能消除静态低速条件下的迟滞效应，在高频跟踪时需要采用其他先进算法来消除迟滞带来的误差。

4 结论

为了设计一种高跟踪精度和高谐振频率的压电式偏摆平台，本文提出了一种二级放大复合柔性铰链结构，在此基础上进行了紧凑型压电式偏摆平台结构设计及其工作原理分析。同时对该平台的偏摆角度进行了解析计算和有限元仿真分析，测试了平台原型的偏摆角和谐振频率以及平台分辨力，并在开环和闭环条件下测试了平台的准静态定位与跟踪精度性能。实验结果表明：在准静态条件下，该平台受蠕变和迟滞等非线性效应的影响较小，可用于低于1.0 Hz参考信号的定位和跟踪。

下一步工作将采用先进的控制算法来研究该偏摆平台在高频跟踪时存在的非线性问题。

参考文献(References)

[1] Beerer M J, Yoon H, Agrawal B N. Practical adaptive filter controls for precision beam pointing and tracking with jitter attenuation[J]. Control Engineering Practice, 2013, 21 (1): 122-133.

[2] 马佳光，唐涛. 复合轴精密跟踪技术的应用与发展[J]. 红外与激光工程, 2013, 42(1): 218-227.

MA Jia-guang, TANG Tao. Application and development of precision tracking technology of composite shaft[J]. Infrared and Laser Engineering, 2013, 42(1):218-227.(in Chinese)

[3] Tian J, Yang W, Peng Z, et al. Inertial sensor-based multiloop control of fast steering mirror for line of sight stabilization[J]. Optical Engineering, 2016, 55(11):111602.

[4] Chen W, Chen S H, Luo D, et al. A compact two-dimensional laser scanner based on piezoelectric actuators[J]. Review of Scientific Instruments, 2015, 86(1): 013102.

[5] 宋盛, 刘重飞, 苑自勇,等. 压电驱动双面快速指向镜的设计[J]. 光学精密工程, 2016, 24(11):2777-2782.

SONG Sheng, LIU Chong-fei, YUAN Zi-yong, et al. Design of double-sided fast steering mirror based on piezoelectric actuating[J]. Optics and Precision Engineering, 2016, 24(11): 2777-2782. (in Chinese)

[6] Jing Z J, Xu M L, Feng B. Modeling and optimization of a novel two-axis mirror-scanning mechanism driven by piezoelectric actuators[J]. Smart Materials and Structures, 2015, 24(2): 025002.

[7] Liu L, Bai Y G, Zhang D L, et al. Ultra-precision measurement and control of angle motion in piezo-based platforms using strain gauge sensors and a robust composite controller[J]. Sensors, 2013, 13(7):9070-9084.

[8] Yuan G, Wang D H, Li S D. Single piezoelectric ceramic stack actuator based fast steering mirror with fixed rotation axis and large excursion angle[J]. Sensors and Actuators A：Physical, 2015, 235:292-299.

[9] 田福庆, 李克玉, 王珏,等. 压电驱动快速反射镜的自适应反演滑模控制[J]. 强激光与粒子束, 2014, 26(1):59-63.

TIAN Fu-qing, LI Ke-yu, WANG Jue, et al. Adaptive backstepping sliding mode control of fast steering mirror driven by piezoelectric actuator[J]. High Power Laser and Particle Beams, 2014, 26(1): 59-63. (in Chinese)

[10] 凡木文, 黄林海, 李梅,等. 抑制光束抖动的压电倾斜镜高带宽控制[J]. 物理学报, 2016, 65(2):154-161.

FAN Mu-wen, HUANG Lin-hai, LI Mei, et al. High-bandwidth control of piezoelectric steering mirror for suppression of laser beam jitter[J]. Acta Physica Sinica, 2016, 65(2):154-161. (in Chinese)

[11] Wang X, Pommier-Budinger V, Reysset A, et al. Simultaneous compensation of hysteresis and creep in a single piezoelectric actuator by open-loop control for quasi-static space active optics applications[J]. Control Engineering Practice, 2014, 33:48-62.

[12] Wang G, Rao C H. Adaptive control of piezoelectric fast steering mirror for high precision tracking application[J]. Smart Materials and Structures, 2015, 24(3): 035019.

[13] Xiang S H, Chen S H, Wu X, et al. Study on fast linear scanning for a new laser scanner[J]. Optics and Laser Technology, 2010, 42(1):42-46.

[14] 徐新行, 杨洪波, 王兵，等. 快速反射镜关键技术研究[J]. 激光与红外, 2013, 43(10): 1095-1103.

XU Xin-xing, YANG Hong-bo, WANG Bing，et al. Research on the key technology of fast steering mirror[J]. Laser and Infrared, 2013, 43(10): 1095-1103.(in Chinese)

[15] Liang Q K, Zhang D, Chi Z Z, et al. Six-DOF micro-manipulator based on compliant parallel mechanism with integrated force sensor[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(1):124-134.

[16] Xu Q. Design of a large-range compliant rotary micropositioning stage with angle and torque sensing[J]. IEEE Sensors Journal, 2015, 15(4):2419-2430.

[17] Wang P Y, Xu Q S. Design of a flexure-based constant-force XY precision positioning stage[J]. Mechanism and Machine Theory, 2017, 108:1-13.

[18] 王耿, 官春林, 张小军,等. 应变式微型精密压电驱动器的一体化设计及其PID控制[J]. 光学精密工程, 2013, 21(3):709-716.

WANG Geng, GUAN Chun-lin, ZHANG Xiao-jun, et al. Integrated design and PID control of micro precision piezoelectric actuator[J]. Optics and Precision Engineering, 2013, 21(3):709-716. (in Chinese)

[19] Xu Q S. A novel compliant micropositioning stage with dual ranges and resolutions[J]. Sensors and Actuators A: Physical, 2014, 205:6-14.