基于非数据通信的导弹编队制导律算法

黄伟， 徐建城， 吴华兴， 李俊兵

(1.西北工业大学 电子信息学院， 陕西 西安 710072; 2.空军工程大学 航空航天工程学院， 陕西 西安 710038)

0 引言

航空飞行器及水面舰艇自主编队作战[1-2]是适应现代战争特点的一种新兴作战模式。其中,导弹编队有效地提高了导弹突防能力、电子对抗能力、协同搜索能力和综合作战效能[3]，可实现对航母编队等重要战略目标的有效打击。

导弹编队飞行过程中，有效地生成和保持预定的编队几何形态，是导弹编队制导律设计的难点。杜阳等[4]基于局部模型预测，设计了飞航导弹队形保持控制器；邹丽等[5]将攻击时间可控制导律与一致性分散化协调算法相结合，提出一种多导弹编队齐射攻击的分散化协同制导方法；韦常柱等[6]采用最优输出调节方法设计了导弹编队最优保持控制器；张磊等[7]基于单领弹编队控制的思想，设计了自适应滑模导弹编队控制器；王品等[8]针对分布式飞行器自组织编队跟踪问题，提出一种有界控制输入的蜂拥编队控制算法；邵壮等[9]采用虚拟结构编队方法，基于李雅普诺夫直接法设计了非线性队形保持控制器；文献[10-12]将虚拟结构法、领从法、行为法等队形控制方法在多智能体一致性算法框架内标准化，提出一种基于2阶动力学模型的飞行器编队控制算法；文献[13-14]研究了存在未知建模误差或未知扰动条件下编队队形的控制问题；文献[15-18]提出一种基于事件触发通信的多智能体一致性算法，有效地减小了编队各成员的信息交互。然而，以上算法在实现过程中均要求编队成员装备具备高吞吐能力的弹间数据链以及传递导弹绝对位置等相关运动参数，在无数据链支持或数据链受干扰而失效的作战环境中，限制了算法的实战化应用。考虑到主动雷达导引头是导弹感知外部环境的另一种重要手段，应用其获取的量测信息实现编队控制将有效地提高导弹编队系统的环境适应性，但设计难点在于：如何仅利用导引头提供的相对运动参数建立制导律算法，实现导弹编队的队形控制；如何保证闭环制导控制系统的渐进稳定性。

本文在非数据通信条件下，基于主动雷达导引头的量测信息，提出一种新的导弹编队制导律算法。首先，描述了领从结构导弹编队控制问题及导弹运动学模型；其次，建立了基于相对运动参数的制导律算法，应用代数图论证明了编队闭环系统的渐进稳定性；最后，推导了制导控制量与导弹控制力之间的关系模型，在控制力作用下实现了导弹编队位置的收敛和速度一致。

1 领从结构导弹编队控制问题描述

1.1 领从结构导弹编队

三维空间中，领从结构导弹编队如图1所示，以地面某点为坐标原点建立北- 天- 东地面坐标系Oxyz，在研究大气层内导弹编队队形控制问题时，可不计地球转动影响，由此将地面坐标系视为惯性系[19]。导弹编队由1枚领弹和2枚从弹构成，建立弹道坐标系Otxtytzt.

假设已在综合考虑编队飞行态势、地形信息和编队实际状态的基础上确定了期望队形，导弹编队过程中，要求领弹与从弹生成并保持既定的相对位置关系和速度关系，由于领弹的主要任务是目标探测和引导编队至指定的目标空域，一般情况下其运动状态不受从弹影响，而从弹运动状态的控制是领从结构导弹编队控制问题的关键。

1.2 导弹编队运动学模型

单枚导弹运动学模型的建立基于如下假设：将导弹视为质点，忽略导弹内部的物理特性、化学特性。作用于导弹的力包括发动机推力、空气动力和重力。为了描述导弹运动状态与作用力之间的关系，将涉及地面坐标系Ogxgygzg、气流坐标系Oaxayaza、弹体坐标系Obxbybzb和弹道坐标系Otxtytzt等多个描述制导问题的坐标系以及各坐标系之间进行转换[19]。在弹道坐标系Otxtytzt中，各轴向加速度与作用力之间的关系式[20]为

(1)

(2)

由此可得，单枚导弹在三维空间中的运动学模型[7]为

(3)

令ξil和ζil分别表示从弹i与领弹l的相对距离矢量和相对速度矢量，则领弹与从弹的相对运动方程为

(4)

2 导弹编队制导律算法

2.1 代数图论基本知识

导弹编队量测网络模型可由有向图描述，有向图由G=(Λ,E)表示：Λ为节点集，E为边集；有向图网络中，若存在节点vi到节点vj的路径，则vi定义为父节点，vj定义为子节点。一条有向路径由一组边(vi,vj)，…，(vn-1,vn)组成,若任一节点到其他节点都存在一条有向路径，则称为强联通有向图；有向树是指有向图中每个节点都存在一个父节点(根节点)，即父节点到其他任一节点都存在一条有向路径，若有向图中至少有一个节点到其他节点都存在有向路径，则称该有向图中包含一棵有向生成树。

令1和0分别表示每个元素均为1和0的n×1列向量，In表示n×n单位矩阵，Mn()表示n×n实数矩阵；邻接矩阵A=[aij]∈Mn()中的各元素表示有向图中各边的权值系数，当(j,i)∈E且j≠i时aij>0，否则aij=0，aij为导弹编队量测拓扑邻接矩阵元素；拉普拉斯矩阵L=[lij]∈Mn()，其中当j≠i时lij=-aij. 当且仅当有向图包含有向生成树，则有向图拉普拉斯矩阵L存在唯一的零特征值，其他所有特征值均具有负实部，1是零特征值所对应的特征向量。

2.2 制导律算法的建立

基于多智能体一致性理论，应用从弹多普勒雷达导引头量测得到的弹间相对运动参数，所建立的从弹制导律算法如下：

(5)

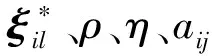
(6)

(7)

定理1在领从结构导弹编队系统中应用从弹制导律算法(5)式，若各枚从弹装备有主动多普勒雷达导引头，则可实时量测每枚从弹与领弹的相对运动参数信息，即拓扑网络中含有以领弹为根节点的有向生成树，且系数η满足：

(8)

式中：υi=-ρ+μi，μi是-L的第i个特征值。则各枚从弹在算式

(9)

所得到的控制力作用下，即可实现导弹编队既定队形的收敛，且各枚从弹与领弹的速度趋于一致，即

证明：假设各枚从弹可实时获得与领弹的相对运动参数，则领弹、从弹所构成的编队量测拓扑中，领弹为有向生成树的根节点，典型结构如图2所示。

(10)

(11)

邻接矩阵A各元素表示有向图中各边的权值系数，若j≠i且从弹i导引头可实时获得从弹j的相对运动参数，则aij>0，否则aij=0. 将各枚从弹作为整体考虑(各枚从弹构成的编队量测拓扑在连通情况下如图2(b)虚线框内部所示)，可得闭环制导控制系统误差方程为

(12)

(12)式为齐次线性方程的标准形式，其解为

(13)

将Σ写为Jordan型，Σ=SJS-1，则

exp (Σt)=Sexp (Jt)S-1,

(14)

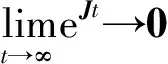
det(λI2n-Σ)=det ((λ2+ηρλ+ρ)In+(ηλ+1)L),

(15)

矩阵-L的特征方程为

(16)

(16)式中μi是-L的第i个特征值，将(15)式写为

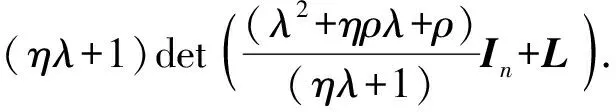
(17)

比较(16)式和(17)式，(15)式特征方程的根可通过求解(18)式得出：

λ2+η(ρ-μi)λ+ρ-μi=0,

(18)

矩阵Σ的特征值为

(19)

式中：ρ>0，根据L的性质有Re (μi)≤0，则Re (-ρ+μi)<0. 令υi=-ρ+μi，根据复数辐角缩放原理[10]，若η的取值满足下列不等式：

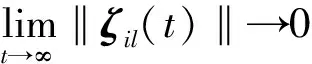
(20)

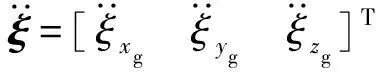
(21)

式中：Tg,t为弹道坐标系到地面坐标系的转换矩阵，由此可得地面坐标系中导弹加速度矢量与导弹控制力之间的关系式为

(22)

(22)式建立了地面坐标系下导弹加速度矢量与弹道坐标系下导弹控制力之间的关系模型，如前所述，假设从弹的飞行控制系统是非惯性系统，则

(23)

结合(22)式和(23)式，可得导弹飞行控制系统为了响应制导控制量u，所需的导弹控制力为

证毕。

定理1成立的充分条件中，要求导弹编队量测拓扑中包含以领弹为根节点的有向生成树，表示各枚从弹导引头可量测获得与领弹之间的相对运动参数。值得注意的是(12)式中定义的拉普拉斯矩阵L，其表示除领弹外，有各枚从弹构成的编队量测拓扑。当导引头视场受到角度限制，导致从弹间量测拓扑失效的特殊情况下，如图2(a)所示，即aij=0，领弹与从弹构成的量测拓扑仍含有向生成树，此时制导律算法蜕变为

(24)

(24)式为带偏置项的比例微分控制算法形式，应用该算法，若系数η满足定理1，则仍可保证编队系统的渐进稳定性，但与(5)式相比较，由于缺少一致性项的作用，将增大编队队形的收敛时间，下面通过仿真过程对二者进行对比。

3 仿真实例

为了验证本文提出的基于测量信息制导律算法的有效性，本节对不同测量拓扑条件下的从弹制导律算法(5)式和(24)式进行对比仿真，仿真条件如下：

1)假设导弹编队包含1枚领弹和2枚从弹，各枚导弹均为质点，从弹飞行控制系统是无迟滞响应的非惯性系统。领弹采用比例系数为3的比例导引法，制导律算式为ul=3vlω，其中ul为领弹的制导控制量、vl为领弹与目标的相对速度、ω为领弹与目标连线的角速度[21]。目标初始位置坐标为(40 km,10 km,40 km)。假设从弹雷达信号处理机应用卡尔曼滤波算法，外推获得的领弹加速度准确、理想。

2)领弹初始位置坐标为(0,10 km,0)，初始速度为(600 m/s,0,100 m/s)；从弹1初始位置坐标为(3 km,12 km,0)，初始速度为(700 m/s,0,200 m/s)；从弹2初始位置坐标(0,8 km,3 km)，初始速度为(800 m/s,0,300 m/s)。

(25)

式中：ε=0.5 km.

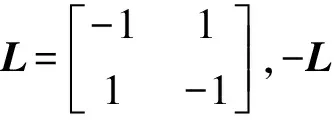
(26)

(27)

为了避免闭环制导系统出现震荡现象，保证系统稳定，(26)式中ρ和η应满足η2>4/ρ，(27)式中应满足η2>4/(ρ+2). 在系数ρ给定前提下，η越大，系统动态响应速度越快，导弹编队队形收敛时间越短，但η取值还应考虑导弹执行机构的物理限制及各轴向最大过载的限制。综合上述分析，仿真过程中设定系数ρ=0.1和η=10.

仿真时间t=100 s. 图3～图7给出了如图2(a)所表示的拓扑条件下，基于算法(24)式，导弹编队各成员运动参数的变化情况。

导弹编队各成员在三维空间的运动轨迹如图3所示，导弹编队由初始位置逐步收敛至既定的编队队形。图4给出了领弹、从弹间距离随制导时间的变化规律，由图4可知，从弹1与领弹的距离及从弹2与领弹的距离随制导时间的增加均趋于理想值。从弹1及从弹2相对预期位置的误差变化规律如图5所示，当t=58 s时，位置误差满足编队队形要求，生成了预期的编队队形，之后为队形保持阶段。图6给出了从弹1在3个轴向与领弹相对速度误差的变化规律，随着制导时间的增加，相对速度误差趋于0. 图7给出了从弹1在地面坐标系3个轴向的指令加速度，各轴向的指令加速度均在限定范围之内，最大过载40g.

图8～图12给出了如图2(b)所示的量测拓扑网络下，基于算法(5)式，导弹编队各成员运动参数的变化情况。

如图8所示，各枚从弹在算法(5)式的控制下，导弹编队队形收敛，既定队形生成时间为t=49 s. 图9给出了编队队形生成过程中弹间距离的变化规律。如图10和图11所示，领弹与从弹间的相对位置误差和相对速度随制导时间逐步趋于0.

图12给出了从弹在地面坐标系中3个轴向的指令加速度，由于一致性项的作用，指令加速度对比算法(24)式明显增大，但均在限定范围之内，再通过算法(9)式的作用，即可得到所需的导弹控制力。算法(9)式中仿真参数设定为：导弹质量m=150 kg，导弹特征面积S=0.1 m2，空气密度ρa=1.293 kg/m3，阻力系数c=0.08，空气阻力计算式为Fd=0.5cρav2S. 图13给出了从弹1在弹道坐标系中3个轴向所需的控制力随制导时间变化情况，由图13可知，各轴向的控制力均在限定范围之内，从弹1在控制力作用下，实现了与领弹位置及速度的收敛。

对比算法(24)式和(5)式的仿真结果可知：1)基于导引头量测信息的两种制导律算法均可实现导弹编队队形的生成和保持；2)由于算法(5)式中一致性项的作用，有效减小了导弹编队队形生成的时间，由58 s缩短为49 s，加快了控制算法的收敛速度。

4 结论

本文提出的制导律算法有效解决了领从结构导弹编队在非数据通信条件下较为特殊的队形控制问题，主要贡献和结论如下：

1)提出了基于导引头量测信息的导弹编队制导律算法，该算法仅利用弹间相对运动参数，即可实现导弹编队队形的生成与保持。

2)基于坐标变换，建立了导弹控制力与制导控制量之间的关系模型，通过构造相对误差项并应用代数图论证明了闭环系统的渐进稳定性。

3)该算法是在无数据链支持的作战环境下，实现导弹编队控制的有益尝试，并为解决数据链受干扰情况下实现编队控制提供了一种新思路。对于导弹编队系统的总体设计具有一定参考价值。

参考文献(References)

[1] 邱华鑫, 段海滨, 范彦铭. 基于鸽群行为机制的多无人机自主编队[J].控制理论与应用, 2015, 32(10): 1298-1304.

QIU Hua-xin, DUAN Hai-bin, FAN Yan-ming. Multiple unmanned aerial vehicle autonomous formation based on the behavior mechanism in pigeon flocks[J]. Control Theory & Applications, 2015, 32(10): 1298-1304. (in Chinese)

[2] Consolini L, Morbidi F, Prattichizzo D, et al．Leader-follower formation control of nonholonomic mobile robots [J]. Automatica, 2008, 44(3):1343-1349.

[3] Cui N G, Wei C Z, Guo J F, et al. Research on missile formation control system[C]∥Proceedings of International Conference on Mechatronics and Automation. Changchun: IEEE, 2009:1496-4202.

[4] 杜阳, 吴森堂. 飞航导弹编队队形变换控制器设计[J]. 北京航空航天大学学报, 2014, 40(2): 240-245.

DU Yang, WU Sen-tang. Transformation control for the formation of multiple cruise missiles [J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 240-245. (in Chinese)

[5] 邹丽, 周锐, 赵世钰, 等. 多导弹编队齐射攻击分散化协同制导方法[J]. 航空学报, 2011, 32(2): 281-290.

ZOU Li, ZHOU Rui, ZHAO Shi-yu, et al. Decentralized cooperative guidance for multiple missile groups in salvo attack [J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(2): 281-290. (in Chinese)

[6] 韦常柱, 郭继峰, 崔乃刚, 等. 导弹协同作战编队队形最优保持控制器设计 [J]. 宇航学报, 2010, 31(4): 1043-1050.

WEI Chang-zhu, GUO Ji-feng, CUI Nai-gang, et al. Research on the missile formation keeping optimal control for cooperative engagement [J]. Journal of Astronautics, 2010, 31(4): 1043-1050. (in Chinese)

[7] 张磊，方洋旺，毛东辉, 等.导弹协同攻击编队自适应滑模控制器设计[J]. 宇航学报, 2014,35(6): 700-707.

ZHANG Lei, FANG Yang-wang, MAO Dong-hui, et al. Adaptive sliding-mode controller design for missile cooperative engagement [J]. Journal of Astronautics, 2014,35(6): 700-707. (in Chinese)

[8] 王品, 姚佩阳, 梅权, 等. 一种基于蜂拥策略的分布式无人机编队控制方法[J]. 飞行力学, 2016, 34(2): 42-46.

WANG Pin, YAO Pei-yang, MEI Quan, et al. Distributed formation control method of UAVs based on flocking[J]. Flight Dyna-mics, 2016, 34(2): 42-46. (in Chinese)

[9] 邵壮, 祝小平, 周洲, 等. 无人机编队机动飞行时的队形保持反馈控制[J]. 西北工业大学学报, 2015, 33(1): 26-32.

SHAO Zhuang, ZHU Xiao-ping, ZHOU Zhou, et al. A formation keeping feedback control for formation flight of UAVs [J]. Journal of Northwestern Polytechnical University, 2015, 33(1): 26-32. (in Chinese)

[10] Ren W. Consensus strategies for cooperative control of vehicle formations[J]. IET Control Theory & Applications, 2007, 1(2):505-512.

[11] Ren W, Moore K L, Chen Y. High-order and model reference consensus algorithms in cooperative control of multivehicle systems[J]. Journal of Dynamic Systems Measurement & Control, 2007, 129(5):678-688.

[12] Wei Z, Cheng D Z. Leader-following consensus of second-order agents with multiple time-varying delays [J]. Automatica, 2010, 46(5): 1994-1999.

[13] Jin T, Liu Z W, Zhou H. Cluster formation for multi-agent systems under disturbances and unmodelled uncertainties[J]. IET Control Theory & Applications, 2017, 11(15):2630-2635.

[14] Hua Y Z, Dong X W, Li Q D, et al. Distributed time-varying formation robust tracking for general linear multiagent systems with parameter uncertainties and external disturbances[J]. IEEE Transactions on Cybernetics, 2017, 47(8):1259-1269.

[15] Dimarogonas D V, Frazzoli E, Johansson K H. Distributed event-triggered control for multi-agent systems [J]. IEEE Transactions on Automatic Control, 2012, 57(5): 1291-1297.

[16] Zhu W, Jiang Z P, Feng G. Event-based consensus of multi-agent systems with general linear models[J]. Automatica, 2014, 50(2): 552-558.

[17] Chen W S, Ren W. Event-triggered zero-gradient-sum distributed consensus optimization over directed networks[J]. Automatica, 2016, 65(3):90-97.

[18] Ge X H, Han Q L. Distributed formation control of networked multi-agent systems using a dynamic event-triggered communication mechanism[J]. IEEE Transactions on Industrial Electro-nics, 2017, 64(10):8118-8127.

[19] 周志刚. 航空综合火力控制原理[M]. 北京:国防工业出版社, 2008: 7-52.

ZHOU Zhi-gang. Aviation comprehensive fire control theory [M]. Beijing: National Defense Industry Press, 2008: 7-52. (in Chinese)

[20] 杨军, 袁博, 朱苏朋, 等.现代导弹制导控制[M]. 西安:西北工业大学出版社, 2016: 60-90.

YANG Jun, YUAN Bo, ZHU Su-peng, et al. Modern missile guidance and control[M]. Xi’an: Northwestern Polytechnical University Press, 2016: 60-90. (in Chinese)

[21] 薛丽华，范宇，宋闯. 现代导弹制导[M]. 北京:国防工业出版社, 2013: 2-20.

XUE Li-hua, FAN Yu, SONG Chuang. Modern missile guidance[M]. Beijing: National Defense Industry Press, 2013:2-20. (in Chinese)