巧用线段图解决问题

线段图是几何直观常见的一种表现形式，在小学数学解决问题教学中经常运用。它可以帮助学生理解题意，分析数量关系，有效促进问题的解决，还能帮助学生架设形象思维过渡到抽象思维的桥梁，以此提高学生分析问题和解决问题的能力。如何让学生正确读图、准确画图和灵活用图就显得尤为重要。下面笔者结合自己平时的教学经验谈几点思考。

一、学会读图

用线段图帮助理解分析题意，是几何直观中数形结合思想在教学中的具体应用，读懂线段图可以帮助学生提高解题效率。

1.提前铺垫。

在小学低年级阶段，一些题目中会出现线段图，这时教师就可以利用这些线段图帮助学生理解抽象的数量关系。教师要教会学生一些简单的读图方法，渗透读线段图的意识，可以借助低段的实物图和线段图的关系，引导学生观察已知哪些信息，要解决什么问题，让学生初步感知线段图与实物、图形、符号一样，都可以表示数量的多少，体会线段图表示数量的简洁性、概括性的特征。经过这样的提前铺垫，能帮助学生逐步树立应用线段图的意识，让学生对线段图不再有陌生感，为后续娴熟运用线段图打下基础。

2.有序引导。

在小学高年级阶段，一些实际问题数量关系比较复杂，教师在教学时可以让学生根据经验，先仔细读图，理解题意，再完成数量关系式。这个读图的过程由教师的点拨引导转向让学生独立完成并解答，逐步培养学生自主读图的能力。

二、学会画图

在苏教版教材中，三年级学习“解决问题的策略”单元时，才第一次真正意义上学习画线段图，这就要求教师相信学生，不怕画错。

1.敢于尝试是前提。

在教学中，很多教师往往为了节省时间，都是自己画线段图或直接呈现准备好的线段图，省去了让学生自主画线段图这一重要的环节，学生成了旁观者，他们并未真正参与到线段图的形成及数量关系的建构过程中去，这样会导致学生画线段图解决问题的能力得不到提升。因此，在解决问题的过程中，教师要舍得放手，充分相信学生，激发学生画线段图的主动性。

2.示范指导是关键。

线段图作为解决问题的“工具”之一，有助于学生提炼、分析数量关系，形成问题解决的方法。但画好线段图对于学生而言却不是一件容易的事，这就需要教师做好示范指导。比如，教师可以先画图，再让学生模仿。在画图过程中，说一说线段图中的信息，比一比线段图中的数据，明确“为什么这样画”，逐步提高学生画线段图的能力。

3.把握关系是重点。

学生要想内化各种画线段图的本领，就需要深入理解题意，明确已知条件和所求问题，找准数量间的对应关系，这是培养学生画线段图解决问题的重点。从“数”到“图”的对应性，“图”与“图”的一致性，再到线段图的科学性和艺术性，都要在此过程中不断磨炼，不断提高。

三、学会用图

1.内化策略。

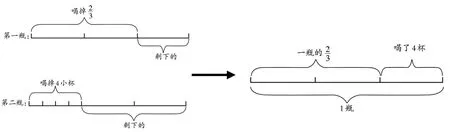
在解决问题后，教师要引导学生利用线段图进行检验，让学生感悟画线段图的优势，并自觉地将之内化成一种策略。例如有这样一道题目：东东和同学聚会时从超市买了两瓶营养快线，他们先把第一瓶喝掉了，接着把第二瓶打开后，又喝掉了满满的4小杯，然后把两瓶剩下的合起来，正好合成了一瓶完整的营养快线。算一算，一整瓶营养快线正好可以倒满多少小杯？

这里的数量关系比较复杂，条件也比较隐蔽。因此，首先要求学生画图呈现两瓶喝掉的量和剩下的量之间的关系，由“两瓶剩下的合起来，正好合成了一瓶完整的营养快线”可知，两瓶喝掉的合起来也正好是一瓶完整的营养快线，即第二瓶喝掉的4杯刚好是整瓶的那么一整瓶营养快线正好可以倒满的杯数是4×3。通过画线段图，数量关系清晰，学生可以深刻体会到画线段图解决问题的优势。

2.寻找错因。

在分析问题时，常常需要根据题目把题意“画”出来，数与形相结合，往往可以更清楚地理解题中的数量关系，启发我们全面分析问题，便于从不同角度去看图与思考，巧妙地解决问题。例如有这样一道题目：甲乙两车同时从相距540千米的A、B两地相对开出，5小时后甲车行了全程的，乙车行了全程的这时两车相距多少千米？

许多学生列式（千米）。这样解答是否正确呢？不妨通过画线段图来检验。

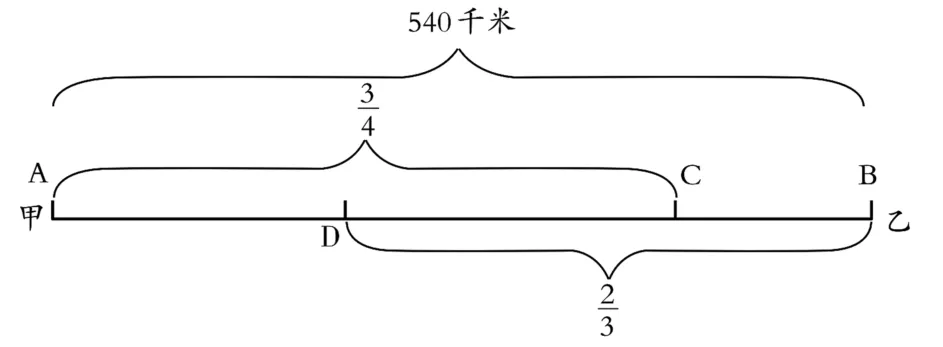
通过画线段图可以一目了然地发现“”所求的却是甲车比乙车多行的路程，并不是两车相距的距离。可见，通过“画”出的线段图可以将学生的思维逐步引向深入。

3.持之以恒。

培养学生综合运用线段图的能力不是一朝一夕的事，需要教师在教学中不断给学生以引导、鼓励和帮助。从低年级到高年级，教师还应综合学生当前的思维发展水平，并根据年龄特点和思维特点因材施教，有目的、分阶段地培养学生借助画线段图解决问题的能力，让学生在解题过程中体悟到数学学习的快乐。

总之，线段图是几何直观中一种重要的数形结合的思想方法，它具有半抽象半具体的特点，既能呈现数学问题的具体情节，又能形象地揭示条件与条件、条件与问题之间的内在联系，把数转化为形，激活学生的数学思维，拓宽学生的解题思路，提升学生在数学学习中的能力和素养。