数学史：人文与理性的融通

□ 刘轩如

一、引言

将数学史融入数学教学，具有知识之谐、方法之美、探究之乐、能力之助、文化之魅、德育之效等教育价值，且这些价值与“四基”“四能”、核心素养、情感与信念紧密相关[1]。因此，数学史在中小学一线受到了越来越多的关注，很多期刊策划了相关的专辑或专栏，很多的成果被人大复印资料全文转载。然而将数学史融入数学教学并不是一件容易的事情，特别是在小学，这与小学生的认知起点比较低，所涉及的历史是早期的，很可能在文献上没有明确的记载有关[2]。那么，能否在史料有限的情况下，开设一节文化气息浓厚且能培养学生理性思维品质的小学数学课？本文将结合“轴对称图形”的教学探索问题的答案。

二、素材分析与应用

对称是不同时代人类试图理解和借此创造秩序、美丽和完美的工具。因此，人类很早就喜爱对称,特别是轴对称，这从早期人类建造的宫殿、创作的艺术品中可见一斑，比如5000～7000年前仰韶文化半坡类型彩陶人面鱼纹盆（图1）、5000年前两河流域出土文物（图2）、故宫太和殿、印度泰姬陵等。不仅如此，对称还广泛地存在于无机界和有机界，对于很多有机界的动物而言，结构上的对称是进化的必然结果，因为为了生存，只有身体的结构左右对称时，它们才能跑得快或飞得高[3]。

图1

图2

尽管有一些与轴对称主题相关的历史素材，但相比于分数、小数等主题的历史素材，这些素材几乎与知识的概念属性无关。因此，基于以上相对较为有限的史料，教师采用“发现对称之美—感受对称之实—探索对称之理—体会对称之用”的思路设计教学，欲实现如下的教学目标。

（1）通过思考、交流、辨析等活动逐步认识轴对称图形，知道轴对称的含义。

（2）在实践操作中发现并认识轴对称图形中的对称轴，并能正确画出对称轴。

（3）在实践操作中提升自身的思维品质，在欣赏与练习中感悟对称的文化魅力与实用价值。

三、教学设计与实施

（一）发现对称之美

师：我们来欣赏一段G20杭州峰会的芭蕾舞表演（30秒的微视频），美吗？为什么呢？

生：很美，演员们跳舞的样子很优美。

生：画面很美，画面都是对称的。

师：芭蕾舞已经很美了，对称让整体的画面看上去更美了，导演是怎么会想到利用对称的美设计这段表演的呢？其实大自然中，就有很多让人感觉到对称的事物，看！

（二）感受对称之实

出示大自然中的图形。

师：有没有想过为什么蝴蝶、蜻蜓和甲虫是对称的？

生：飞得稳，爬得稳。

师：大自然中让人感觉到对称的事物还有很多，我们人类也很早就从大自然中发现了对称的美，并且把这些美用他们自己的方式记录了下来，看！这是大约7000年前人类制作的彩陶盆（图1），还有彩陶上的人面鱼纹，是不是对称的呀？5000年前，两河流域的先民们早已经广泛使用了对称的美，从一些出土的文物（见图2）中我们就可以看出。1500年前的敦煌莫高窟的壁画（见图3）上也记载着迷人的对称美！

图3

师：更神奇的是从古至今、从中到外的许多优秀的建筑设计都用了“对称”。比如，大约500年前意大利建筑大师设计的作品和后人模仿改良的建筑（见图4），故宫的太和殿和印度的泰姬陵。

图4

师：（出示图5）看这是什么？对了是剪纸！但很少有人知道安徒生也是“剪纸大师”！这位诗人总是随身带着一把剪刀，用剪纸取悦大人和孩子。他一面说故事一面剪纸，剪纸完成时，故事也讲完了。故事的高潮便是他把神秘的剪纸打开，展现出最后的图案。他的一幅幅剪纸就是一篇篇童话。

师：还有我们的双喜剪纸，都给人对称的感觉。

图5

（三）探索对称之理

1.独立操作。

师：那么小朋友们，你能剪出一个对称图形吗？好，请每一位同学从学具盘里拿一张彩纸，看你有几种方法剪出一个轴对称图形，我们比一比哪一种方法最好。

2.学生分享。

学生展示作品，见图6。

图6

师：第一幅图你是怎么剪的？

生1:我就是一对折，然后剪一个图形，打开以后就是这个图形了。

师：怎么证明你剪出的图形是对称的？

生1：这个图形，对折，左右能够重合就说明它是对称的。

师：第二幅图是谁剪的？你剪的是什么？

生2：我剪的是飞机，也是先把纸对折，然后在折痕旁边画飞机的一半，最后把纸打开就是这个飞机了。

师：其他的几幅图也是这么画的吗？

生：对！

师：小朋友们真厉害，通过折一折剪一剪，剪出了一个这样的对称图形，其实，像这些，将一个图形通过对折一次后，两边的图形完全重合，在我们的数学中就叫作轴对称图形。轴在数学中表示一条直线。看，对折时，这里留下的一条折痕叫“对称轴”。

师：为什么叫它对称轴呢？

生：轴表示一条直线，对称表示两边重合。

师：那么轴对称又是什么呢？

生：轴对称指的是黑板上这种，对称的图形，指的是一种图形。

师：对！轴对称图形指的是像这样的图形，对称轴指的是这条折痕，是一条直线！

师：对称轴我们可以用一条直线来表示，直线画在纸上又是用线段来表示的，线段的长度要超过图形。请你画一画刚才你剪的轴对称图形中的对称轴。

（四）练习巩固

1.从交通标识中选取5个图形让学生判断是否为轴对称图形，并说明理由。

2.从少先队队徽中抽取基本图形五角星和圆（见图7），让学生判断这两个轴对称图形对称轴的数量。

图7

（五）体会对称之用

1.利用方格纸找出五角星的对称轴。

2.绘制轴对称图形（作为课后练习）。

师：老师在准备五角星的时候，不小心打翻了墨汁，有一半的五角星被涂掉了（出示图8）！小朋友们快帮我想想办法，怎样在这个五角星的基础上补全另一半呢？

图8

（六）课堂小结

师：今天大家有什么收获？

生：我知道了对称轴是轴对称图形当中隐藏的一条线。

生：我知道了生活中有很多对称的图形。

四、学生反馈

课后，对班级32名学生的问卷调查与课后练习进行统计，掌握了如下学情。

1.学生对对称之用背后的缘由有了一定的认识。

针对“为什么很多昆虫，比如蝴蝶、蜻蜓、甲虫的身体都是对称的”的提问，有24名同学认为与保持平衡有关，如“如果它们不对称，飞起来就会斜”“因为这样才能保持平衡”“因为如果不对称的话，昆虫就容易掉下来”“因为只要它们一边重，一边轻，飞的时候就会掉下来”；针对“有很多建筑大师将轴对称图形应用于建筑设计，请你说明其中的原因”的提问，有23名学生感受到了生活中有那么多对称的建筑设计或艺术作品是对称之美，如“原因是这样做很美观”“看起来好看”“因为这样的设计具有古典美感和次序感”。

2.学生基本上掌握了这节课的知识内容。

针对“请你写出已学的找轴对称图形对称轴的方法，并画出正方形所有的对称轴”的问题，虽只有5名学生回答了前一问题，“方法1，折一折；方法2，量一量”“可以折的就把它对折，能够合起来的线就是它的对称轴，不能合的就用尺量中间的数（所在的点）就是（对称轴经过的点）”“把图形对折，如果重合，那么就是轴对称图形，对折的那条线就是对称轴”“方法1，对折，如果两边完全重合的话，中间的折痕就是这个图形的对称轴；方法2：先量出这个图形一边的长度，再量出一边一半的长度”，有28名学生正确地画出了正方形中的4条对称轴，其余4名学生正确地画出了部分对称轴。对于课后练习“根据对称轴，画出轴对称图形（如图9）的另一半”的题目，完全正确的有16人，15人因未能找到不在格点上的一点的对称点而未能补全图形，未做对的只有1人。

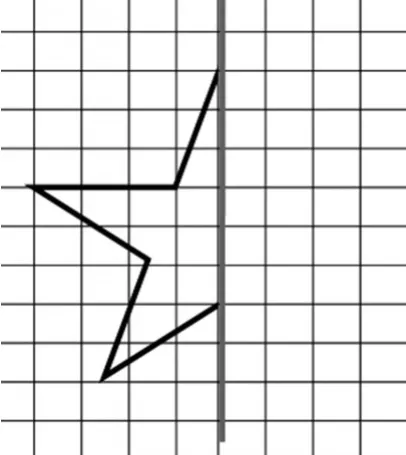
图9

3.学生有了积极的情感体验，对这节课的评价较为多元。

在对问题“当你得知丹麦的安徒生不仅是伟大的童话大师，还是剪纸大师时，你有什么感想”的回答中，大部分学生（94%）都相当震撼，“原来童话大师也能剪出这么棒的剪纸呀！”“我觉得安徒生好厉害”。对于问题“这节课，你印象最深的是什么？为什么”的结果统计发现，学生对这节课的认识较为多元，且视觉感受与动手操作带来的影响较大，分别占总数的30%左右。

五、结语

将数学史料融入“轴对称图形”的教学，引导学生在社会与自然、艺术与建筑、古代与现代的交织中感受对称的文化魅力与实用价值；通过课后的调查发现学生在视觉直观与动手操作中，较好地掌握了轴对称图形与对称轴。同时，“发现对称之美—体会对称之实—探索对称之理—感受对称之用”的思路遵循知识发生、发展的过程，也大致与学生的认知发展规律相一致，因此，按照这一思路实施教学，会让学生感受到数学知识的学习是一件自然而然的事情，数学学习是发现规律、解决问题的过程，这将有助于学生思维品质的培养。因此，“轴对称图形”算得上一节文化气息浓厚且能培养学生理性思维品质的小学数学课。

小学数学呼唤文化气息浓厚且能培养学生理性思维品质的课堂，因为这样的课堂既能培养学生的关键能力，又能培养学生的必备品格。在今后的教学中，我们不妨以核心素养的培养为基，在课堂中适当地融入与教学主题密切相关的数学家解决问题的方法，甚至是错误的方法、数学家的故事，让这些数学史上的人物、事件真正发挥“课堂中一名额外学生”的价值，让学生在和古人的“对话”中得到发展。

参考文献：

[1]Wang,X.,Qi,C.&Wang,K.A Categorization Model for Educational Values of the History of Mathe⁃matics:An Empirical Study[J].Science&Education,2017,26(7-9):1029-1052.

[2]岳增成，沈中宇.HPM与小学数学教学核心问题探索——汪晓勤、邹佳晨老师访谈录[J].小学教学（数学版），2017，（11）：4-9.

[3]汪晓勤.数学文化透视[M].上海：上海科学技术出版社，2013：1-8.