当中学数学实验遇到微课

江苏省黄埭中学 程仕然

中学数学实验者，中学数学教学中的“屌丝”也。它没有数学起始课那种“萌萌”的面孔，没有概念课那种小鲜肉式的招人喜爱的身材，也没有习题课那样强硬的后台背景，更没有复习课那样“高大上”。它是不折不扣的屌丝，没人爱，没人理睬。遇到微课，这将是它人生的转折。

微课者，八面玲珑，清新可人小女子也。其一，身材娇小（时间短），人人喜爱；其二，思想单纯（内容较少），好相处；其三，家门不高（资源容量较小），容易接近；其四，喜形于色（情景化），让人一看就“透”；其五，个性鲜明（主题突出、内容具体）；其六，衣着大众（内容草根）；其七，要求不高（成果简化、多样传播），好养活；其八，热情似火（反馈及时，趣味创作）。

微课具有的这些特点，无一不是中学数学实验所渴望得到的。

长期以来，中学数学实验都不受广大教师待见，原因不外乎下面几种：

1.解题教学派：弄这东西有什么意思？还不如直接讲几道题来的实惠。

2.质疑派：数学实验这东西对学生能起多大作用？做和不做实验有什么区别？

3.彷徨派：教学时间这么紧，会影响教学进度的。

4.打假派：用动画画一个椭圆图象，让学生观察出椭圆定义，这是“伪实验”。

智者说：误解源于不了解。数学课堂教学的过程是提出问题、解决问题、提出新问题、解决新问题的过程，进行数学实验的意图是为了引导学生提出问题。因此，以实验为载体，展示数学生长过程，使学生亲历数学知识的探索之旅，让学生从实验中提出数学问题，获得数学知识。

当中学数学实验与微课结合起来后，数学实验才会大放光彩，作用和效果也是普通课堂所不可比拟的。

【数学实验微课案例1】数学实验得出线面垂直的判定定理片段

教师：用定义证明线面垂直时，在平面内的任一条直线代表平面内的所有直线，由于它位置的任意性，也给证明带来了不便，那么还有没有更简便的方法判定线面垂直呢?

折纸实验：

1.过△ABC的顶点A进行折叠，折痕为AD，将翻折后的纸片竖起放置在桌面上（如图1），BD，DC与桌面始终接触且不在同一直线上。进行观察并思考：折痕AD与桌面垂直吗？

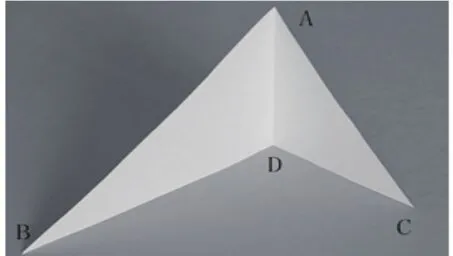
图1

图2

2.作BC边上的高，垂足为D，沿AD翻折纸片，将翻折后的纸片竖起放置在桌面上（如图2），BD，DC与桌面始终接触且不在同一直线上。观察并思考：折痕AD始终与桌面垂直吗？

案例分析：本实验把线面垂直的判定问题隐含于折纸实验中。实验初，教师提出问题，为引出线面垂直的判定定理做铺垫。实验中，思考提问、引导学生实验，渗透无限（任意垂直）与有限（两条相交垂直）的转化思想。让学生通过直观感知，引导学生归纳出线面垂直的判定定理。发挥了数学实验的作用，让学生充分体验到现实中数学知识的发生、发展。这个过程不仅解决了数学问题，也为学生解决无限向有限转化和化归提供了思维范式。

本内容拍成视频，学生可以在课前、课堂上进行反复观看、观察，也可以跟随视频自己操作、探索，感受数学实验的魅力和快乐。

【数学实验微课案例2】椭圆概念数学实验教学片段

展示实验用品：一段结成圈的细线，一支笔，两个大头钉。

教师：我们知道，毛驴（动点）拉磨（定点）是个圆（边说边比划）。下面我们来做一个小实验，看看毛驴（动点）拉双磨（两个定点）会是什么？学生笑，很兴奋，很好奇。教师：我们先把两盘磨（两个定点）安放好，小毛驴走起，大家注意观察哦（如图3）。请告诉我这个图形是什么？，仿照圆的说法，你还能给出椭圆的定义吗？……

图3

案例分析：本实验中，学生经历了：疑问（问题提出：这堆东西能干什么？产生认知冲突）——操作与观察（动手去探索，体验椭圆图形产生的过程）——思考（提出问题：椭圆是什么？再次产生认知冲突）——探索（类比圆的生成和定义，进行知识的类比和迁移）——解疑（问题解决，生成椭圆定义）——自信（自己亲身经历椭圆图象的产生及椭圆定义的给出过程。原来数学就在身边，我也可以做得到）——跃跃欲试（研究了这些东西，有成就感，怎么也得再往下探探看）。教师成功地给学生创造了一个数学学习和研究的微环境，让学生观察椭圆产生过程并回答图形是什么，引导学生自己提出问题；通过与圆的定义来类比解决椭圆的定义恰好是与学生经验内容相融合。

椭圆定义是中学阶段几个最重要基础的概念之一，很多人上过，也有比较精彩的课例。然而，一届又一届的高中毕业的学生，有几个学生能利用简单工具独立画出完整的椭圆呢？原因是什么？很多老师只是照课本讲讲，或者用动画简单演示一下，进行所谓的“观察实验 ”，这些很难让学生对相关内容有深刻、深入的理解，更谈不上思维层次的提高了。

本段内容，学生既可以通过反复播放视频，观察实验视频，也可以在视频指导下，在课堂或课后独自进行实验探索。这些情况，是传统课堂无法完成也无法达到效果的。

所以，当中学数学实验与微课结合起来后，让中学数学教学吹进了一股清新的风，为中学数学课堂教学模式又注入了新鲜血液。数学实验通过短小微视频的方式给学生的学习和教师的教学带来了帮助与便利。视频内容，学生可以学习，也可以借鉴，还可以超越，更可以有更好的点子和想法，这些也在改变学生的学习方式和学习思维。也许大家所说的翻转课堂，就是此意吧。