SPSS软件在导弹武器系统费用预测中的应用

尹江丽，杨晓丹

(航天工程大学 基础部， 北京 101416)

对于武器系统费用分析,目前尚未有统一的定义[1]，美国布兰查德教授称之为寿命周期费用分析(life cycle cost analysis,LCCA)，他认为寿命周期费用分析是一种系统分析方法,用于选择和确定装备等有限资源的最佳费用,并为此而对各种方案做出必要的评价。导弹武器系统的费用分析研究是武器系统费效分析评价决策的基础。传统的分析方法主要采用建立完整的费用线性模型，要求样本量大且具有较好的分布规律，预测结果与实际相差较大[2]。分析建模方法是建立在过去研制导弹武器的经验基础上去预测推断待研制导弹武器系统的费用问题。在导弹武器系统的费用研究中，数理统计方法起着不可或缺的作用，尤其是统计学中的回归分析理论是费用预测应用最多的工具之一。

回归预测模型的计算方法很多，通常采用手工计算、Excel、Matlab等方法，但由于指标所受制约的因素往往很多，所以需要收集的数据也很多，从而导致计算过程复杂、繁琐。SPSS (Statistical Product and Service Solutions)是当前世界上流行的统计分析软件之一，具有强大的数据处理功能、方便易用的用户操作方式、灵活的表格分析报告，是公认的比较优秀的统计分析软件[3]。

由战术导弹系统分析可知[4]，影响导弹费用的因素主要有：导弹的质量(包括导弹载体和有效载荷的质量，单位kg)、导弹的最大速度(单位Ma)及导弹的最大射程(单位海里)等，本实验采用SPSS软件，对影响导弹费用的一些因素进行多元线性回归，通过一系列的检验方法，剔除对导弹费用影响不明显的参数后，建立合理的多元线性回归预测模型，以便能够合理准确地预测待研制导弹武器系统的费用。

1 基本原理

线性回归分析是基于最小二乘原理产生的统计分析方法，用来研究一个或多个自变量(因素)与一个因变量(指标)之间是否存在线性关系。若影响指标的因素只有一个，即只有一个自变量，就是一元线性回归，若影响指标的因素有多个，则为多元线性回归。多元线性回归的数学模型为

(1)

此模型用来解决以下几个问题：① 通过样本估计出β0、β1、β2、…、βp的近似值，确定因变量与自变量之间的关系表达式；② 通过假设检验的方法对因素进行分析，影响不显著的因素可以剔除；③通过控制自变量的数值，借助于数学模型预测或控制因变量的取值和精度[5]。

2 回归模型及分析

收集22种各种型号导弹费用的相关数据[4](见表1)，根据这些数据，建立费用的估算模型。

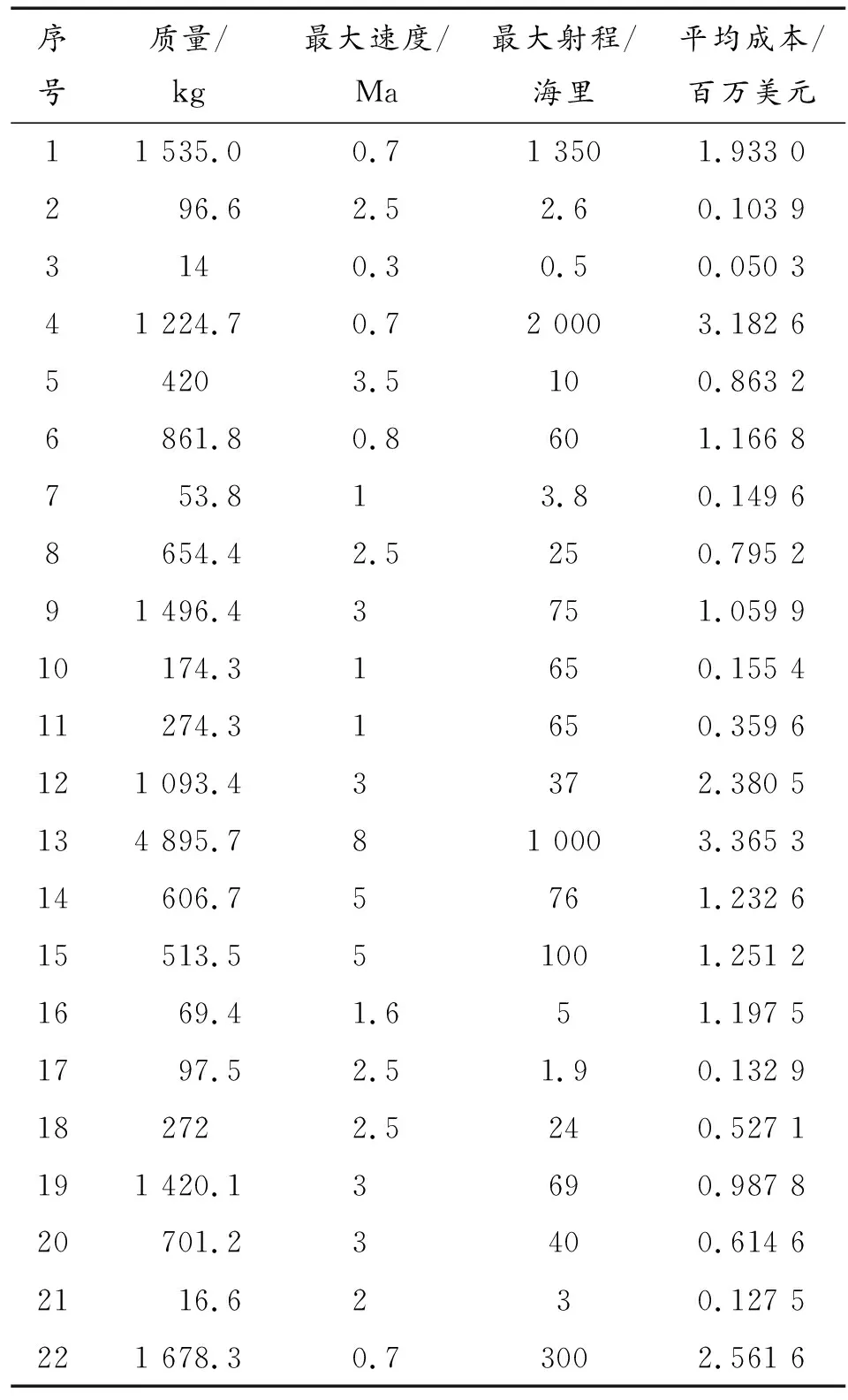
表1 22种导弹的费用数据

利用SPSS统计分析软件，采用线性回归模型对平均成本和导弹质量、导弹最大速度及导弹最大射程进行回归分析，选取平均成本y为因变量，导弹质量x1、导弹最大速度x2、导弹最大射程x3作为自变量。

SPSS回归分析过程为：首先在SPSS的数据编辑窗口输入分析数据，然后在“分析” 菜单中进入“回归”， 选择“线性”，弹出线性回归参数设置对话框。将左侧列表框中“平均成本”变量添加到【因变量】列表框中，同时将“导弹质量”、“最大速度”和“最大射程”变量添加到【自变量】列表框中，在方法栏中选择“进入”；单击“统计量”按钮，进入统计量对话框，分别启用【估计】、【描述性】、【模型拟合度】和【Durbin-Watson】复选框，并单击“继续”按钮，回到线性回归对话框；其余使用默认选项，单击“确定”按钮运行程序[6-7]。

SPSS输出的线性回归分析结果如下：

1) 相关性分析

相关性分析主要显示了各个自变量和因变量之间的关系紧密程度，数据越接近于1，表明两者相关程度越高。从表2中可以看出，平均成本与最大速度的相关性不大。

表2 变量之间的相关性分析结果

2) 拟合优度检验和残差的自相关检验

表3 拟合优度检验和残差的自相关检验结果

3) 回归模型的显著性F检验

此检验的目的是：检验所有自变量与因变量之间的线性关系是否显著。从表4可以看出，F统计量的值为17.279，显著性水平的P值几乎为零，说明在所有自变量的共同作用下，与因变量之间的线性关系显著。

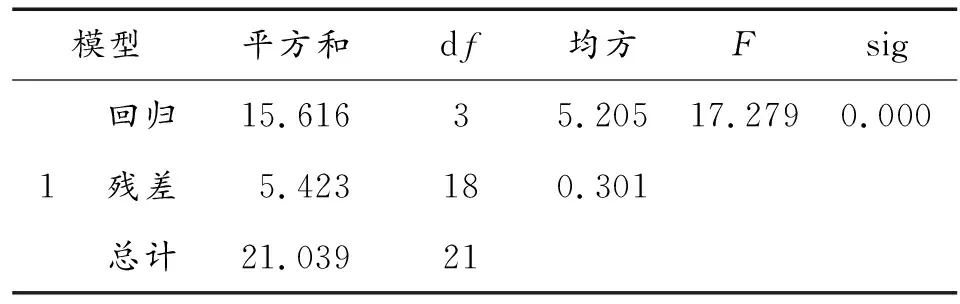
表4 回归模型方差的F检验结果

4) 回归系数的显著性t检验

此检验的目的是：检验每个自变量对因变量的影响，不显著的予以剔除。从表5可以看出，此回归模型中最大速度的t值较小，检验的p值为0.978,大于显著性水平0.05，故此变量对平均成本的影响不太显著，应该剔除。由此可以看出，模型虽然通过了显著性F检验，但很有可能不能通过变量的显著性检验。

表5 回归系数的显著性t检验结果

5) 残差分析

表6显示了预测值、残差、标准化预测值、标准化残差的相关数据，根据概率的3σ准则，标准化残差的绝对值最大为2.397，小于3，说明样本数据中没有异常值。

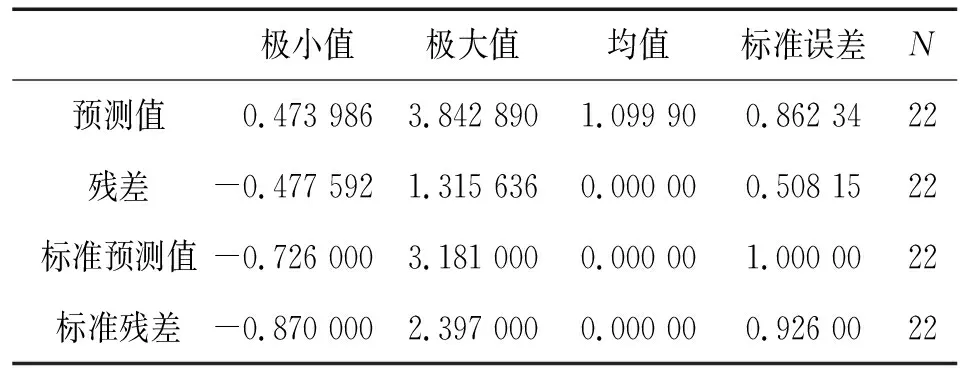
表6 残差分析结果

6) 最终预测模型

模型剔除导弹最大速度x2后，用本次实验中使用的方法和步骤重新对平均成本y，导弹质量x1、导弹最大射程x3作进行线性回归分析。得到的主要结果如表7～表10所示。

表7 剔除x2后拟合优度检验和残差的自相关检验结果

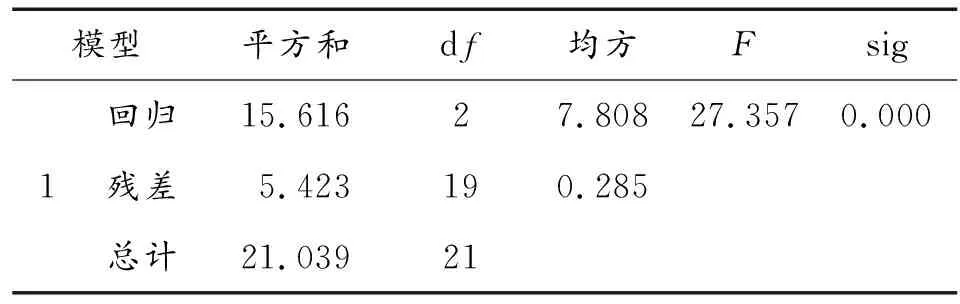
表8 剔除x2后方差的F检验结果

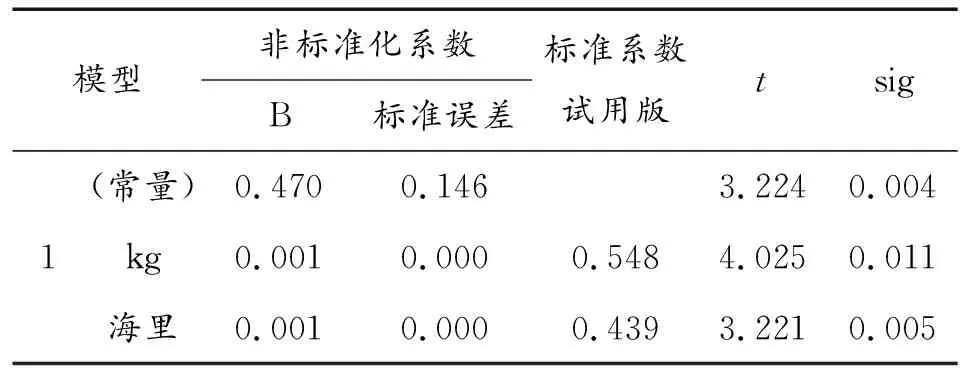
表9 剔除x2后回归系数的显著性t检验结果

表10 剔除x2后残差分析结果

从表7～表10可以看出：剔除变量x2后，模型的拟合优度和DW值变化不大，拟合效果很好且变量无序列相关性；方差的F检验与原来模型结论相同，自变量与因变量之间线性关系显著；与原来的模型相比，变量x1和x3均通过了显著性t检验，因此模型更加合理，故最终的预测模型为

y=0.470+0.001x1+0.001x3

(2)

假如已知某型号导弹质量为984.5 kg，最大射程为80海里，则可以预测其成本约为

y=0.470+0.001×984.5+0.001×80=1.534 5(百万美元)

3 结论

利用SPSS软件对导弹成本进行回归分析，建立回归模型，通过对模型的一系列检验，剔除较弱关系的自变量，对模型进行修正后最终给出了导弹平均成本的预测模型，SPSS回归分析是导弹费用指标测定的一种有效方法。

[1] 于向军，王伟海.武器系统费用分析的发展现状及对策建议[J].军事经济研究，2012(1)：50-52.

[2] 杨志刚，王海涛.舰空导弹武器装备寿命周期费用分析[J].兵工自动化，2013(10)：4-7.

[3] 杨光霞.SPSS数据统计与分析[M].北京:清华大学出版社,2014:203-208.

[4] 文仲辉.战术导弹系统分析[M].北京:国防工业出版社,2000:274-275.

[5] 滕素珍.数理统计学[M].大连:大连理工出版社,2005:172-244.

[6] 冯国生.SPSS统计分析与应用[M].北京:机械工业出版社,2014:84-96.

[7] 汤泽姣，朱克喜.基于SPSS回归分析对中长期居民用电负荷预测 [J].贵州电力技术,2010,13(7):24-27.