机器人运动学的空间解析方法研究

陈 洪

(福建省三明市东辰机械制造有限责任公司，福建 三明 365500)

0 引言

机器人在各行各业中的应用越来越广，机器人逆运动学是机器人应用中的重要环节和主要方式，机器人的逆解问题又是机器人逆运动学的基础。逆解问题即已知机械臂末端的位置和姿态，求各个关节角，通常一种末端姿态对应多组关节角度。逆解问题的传统解法是采用坐标变换方法，即首先为每个连杆建立一个坐标系，然后建立操作臂逆运动学方程，再通过坐标逆变换，经过人工观察挑选可以求解的方程，最后对该方程进行求解[1]。如果机器人在狭窄空间中作业时则需要先计算出关节的角度再确定机器人的整体形态[2]。本文提出的空间解析方法采用与坐标逆变换法相反的次序来求解运动学问题，即根据机器人连杆的相对运动关系，在笛卡尔空间建立一个关于关节点坐标的数学模型，求解得到关节点的坐标，然后再根据机器人的结构特点计算出关节变量，可以优先确定机器人的整体位形。

1 空间解析方法

空间解析方法是以各个关节点的坐标为目标建立数学模型。

1.1 位置分析

关节点的选取原则是：关节轴线方向与连杆方向一致的关节不设为关节点，连接相邻连杆在同一平面的关节设为一个关节点；如果前面连杆连接关节轴线方向与连杆方向一致的关节时，设为两个关节点，其他情况仍设为一个关节点。

在机器人机构中常用到的关节有转动关节和移动关节。转动关节如图1所示，Pi(xi,yi,zi)为关节端点的位置，Zi为关节轴线，关节点Pi+1绕Zi转动，Pi+1的位置可以由空间圆环方程表示，即：

(1)

关节轴线Zi可由其前面的关节点及结构形式表示，即：

(2)

其中：γi为Zi与Zi+1的结构夹角。

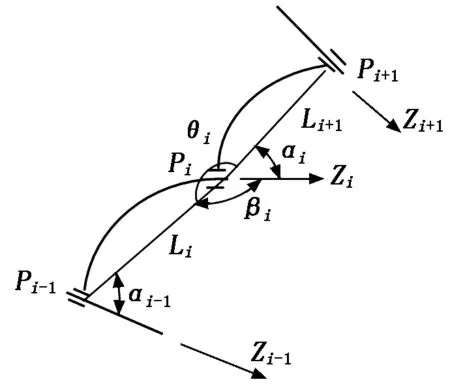
图1 转动关节

移动关节如图2所示，关节点位置可以由空间参数方程表示：

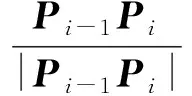
(3)

式(3)中移动方向Zi可由其前面的关节点及结构形式表示，如式(2)所示。

通过上面的分析，可以对任意一个机器人系统在笛卡尔空间建立数学模型，求解出关节点的坐标位置后，各个关节变量可以用矢量积方法求出转动关节的转角θi和移动关节的移动量Li:

(PiPi+1×Pi+1Pi+2)·(Pi-2Pi-1×Pi-1Pi)=|PiPi+1×Pi+1Pi+2|·|Pi-2Pi-1×Pi-1Pi|·cosθi.

(4)

Li=|Pi-1Pi|.

(5)

对于转动或移动方向，可以通过验证关节点的坐标值来确定。转动关节和移动关节结构确定后，γi、αi、βi、αi-1都是已知量。

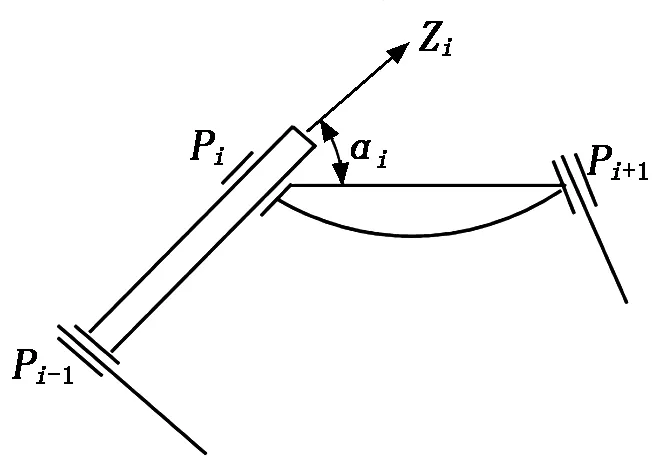
图2 移动关节

1.2 速度分析

对建立的数学模型通过求导可得到机器人关节位置的速度模型：

(6)

首、末关节点的速度已知，整理后写成矩阵形式为：

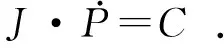
(7)

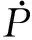
由式(7)得到关节点速度为：

(8)

得到关节点的速度后，可利用相邻关节点之间的相对速度得出关节变量速度：

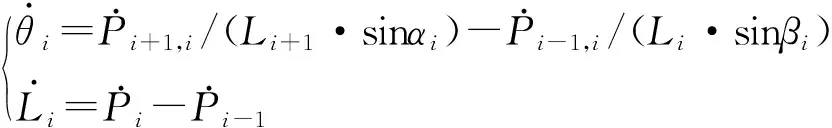
(9)

2 应用实例

以PUMA560机器人为例，根据机器人的结构，确定各个连杆的端点p0～p4和手抓中心点p2。建立的PUMA560机器人关节坐标系及结构参数如图3所示。其中关节4、5、6构成腕关节，即3个关节的旋转轴交于一点。端点p1相对于基坐标系不变，即p0(0,0,0)、p1(0,0,660.4)，未知端点为p2、p3、p4，其他参数为d2=149.09 mm，d4=433.07 mm，d6=56.25 mm，a2=431.8 mm，a3=20.32 mm。

已知手爪的位姿为：

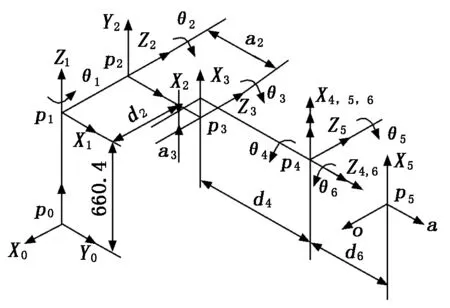
图3 PUMA560机器人的结构参数

根据手爪的位姿，可以得到p4点坐标值为(300,340,200)，通过上面的运动位置分析，可得到p2、p3点的坐标值，再根据结构特点求出对应的关节角，如表1所示。

表1 p2、p3点的坐标值及关节角度

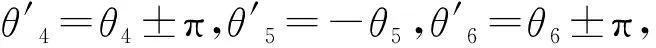
3 结语

通过上面的实例，证明了此方法对机器人求逆解是可行的。该方法通过引入关节点位置为目标，易于分析机器人系统的整体位置及其运动趋势，为机器人在操作空间中的非碰撞轨迹规划提供了一种新思路，此方法具有一定的实用性，可以应用到其他机器人系统中。

参考文献：

[1] 蔡自兴,谢斌.机器人学[M].北京：清华大学出版社,2015.

[2] 权龙哲.狭闭空间内苗盘物流化搬运机器人运动规划与试验[J].农业机械学报,2016,47(1):51-59.