一种新的大型变桨轴承寿命计算方法*

李润林，杨明川，段博志，邹荔兵，贺小兵，张 伟

(1.青海东方华路新能源投资有限公司，青海 西宁 810000；2.明阳智慧能源集团股份公司，广东 中山 528437)

0 引言

兆瓦级以上大型风力发电机组通常选用双排四点接触球轴承[1-2]，由于变桨轴承的工程算法在计算时无法考虑轴承套圈的变形对滚动体载荷和轴承寿命的影响，因此计算结果偏向于保守[3]。对于变桨轴承的有限元计算，以往的研究要么采用半实体模型的有限元方法 ，要么采用简化滚动体的有限元方法。采用简化滚动体有限元方法在计算变形时较为合适，但是在计算寿命和应力时会有一定的误差。采用半实体的有限元模型计算不同的载荷时需要找到不同的对称面[4]，否则在同一对称面内计算会导致滚子的受力位置不正确，且有限元计算方法无法直接计算出一批轴承的90%可以达到的寿命，这对于结果的实际应用是一个缺陷。因此本文提出一种结合工程方法和有限元方法的新的计算大型变桨轴承寿命的方法。首先建立变桨轴承的全实体有限元模型，并验证建立模型的准确性；再将变桨轴承的载荷施加到全实体有限元模型中进行求解，得到轴承每个滚动体承受的载荷；最后再将每个滚动体承受的载荷代入到结合ISO16281标准的工程算法中进行计算，从而得到变桨轴承的寿命。

1 大型变桨轴承有限元模型

本文以某MW级变桨轴承为例，论述如何建立变桨轴承的有限元模型。采用半实体的有限元模型需要在载荷的对称面上施加对称约束，计算不同的载荷就需要找到不同的对称面，否则在同一对称面内计算会导致滚子的受力位置不正确，而且对称面定义准确与否也是影响计算结果的重要因素，采用简化模型会导致计算接触应力不准确[5]，因此本文采用全实体有限元模型来建模。

1.1 有限元模型的建立

首先采用SolidWorks建立变桨轴承的几何模型，然后将轴承的几何模型导入到专业的前处理软件Hypermesh中进行几何处理并划分网格，从而建立有限元模型，最后将有限元模型导入到经典ANSYS中进行静力学设置和求解。对于模型中一些小的特征，如圆孔、倒角，由于其对结果影响比较小，建立有限元模型时将其删除。

变桨轴承内、外圈和滚动体均采用20节点的六面体单元Solid186单元划分网格。在滚道的接触部位为了保证计算精度，将网格进行局部加密；对于非滚动的接触部位采用较粗的网格划分。轴承的弹性模量E=2.1×105MPa，泊松比μ=0.3，密度为7 850 kg/m3。建立的轴承有限元模型如图1所示。

图1 轴承的有限元模型

1.2 接触的建立

在同一个方位角2个滚动体跟滚道之间会形成8个接触对，而且接触部位随着载荷的变化会发生接触或者脱离，这是一种高度非线性的行为。在受载前无法确定滚子接触部位，当载荷发生变化时，接触的滚动体也会发生相应的变化，因此为了准确地模拟出这种接触关系，需要对每一个接触分别单独建立接触关系。由于轴承单排有93个滚子，因此总共要建立744个接触对，这就需要在ANSYS中通过APDL命令流的方式来建立，否则很容易出错。为了更好地保证计算的精度，对目标单元采用Target170单元、接触单元采用Contact174单元进行划分。在如图2所示的1～8沟道分别建立标准接触，用来模拟滚动体的传力过程。

1.3 边界条件及加载

变桨轴承工作时承受径向载荷、轴向载荷、倾覆力矩三者的共同作用，因此在计算时需要同时加载这3个载荷。在变桨轴承内圈中心建立一个加载点，对这个加载点施加径向载荷、轴向载荷和倾覆力矩，如图3所示。变桨轴承工作时，圈与轮毂通过螺栓的预紧力连接在一起，因此可以认为变桨轴承的外圈固定不动，对轴承外圈与轮毂连接部位施加全约束，由于此次建模忽略了保持架，为了模拟保持架对滚动体的支撑作用，在滚动体和保持架配合处约束其圆周方向的自由度。

2 有限元模型验证

通过对工程算法计算的赫兹接触应力与本文有限元方法计算的赫兹接触应力进行对比可以验证本文有限元计算方法的准确性。

当变桨轴承承受纯轴向载荷900 kN时，用工程算法计算得到的赫兹接触应力为1 429 MPa,用本文的有限元法计算得到的赫兹接触应力为1 394 MPa(如图4所示)，误差为2.4%。

当变桨轴承承受纯径向载荷500 kN时，用工程算法计算得到的赫兹接触应力为882 MPa,用本文的有限元法计算得到的赫兹接触应力为847 MPa(如图5所示)，误差为3.9%。

图2 滚道接触部位示意 图3 变桨轴承加载面

当变桨轴承承受倾覆力矩5 500 kNm时，用工程算法计算得到的赫兹接触应力为1 929 MPa, 用本文的有限元法计算得到的赫兹接触应力为1 848 MPa(如图6所示)，误差为4%。

从以上对比中可以看出，采用有限元算法和工程算法计算误差不大。有限元算法由于考虑了轴承内、外圈的变形，因此滚子受到的接触应力比工程算法小，两者之间的最大误差在5%以内。因此本文采用的这种计算方法准确度得到了验证，可以采用此方法进行后续的分析。

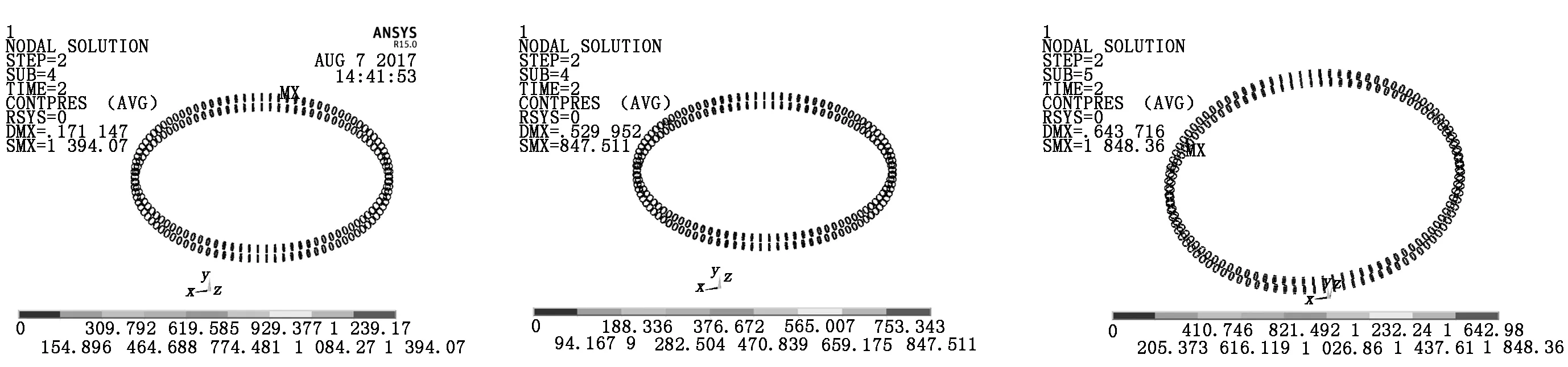
图4 轴向载荷下赫兹接触应力 图5 径向载荷下赫兹接触应力 图6 倾覆力矩下赫兹接触应力

3 大型变桨轴承寿命计算

3.1 滚道载荷的提取

在有限元分析中轴承是通过滚动体和内、外圈的接触面进行载荷传递，因此提取滚道上的载荷时只需要提取接触面上的载荷就可以满足要求。在ANSYS中通过结果的后处理可以直接提取单个接触面的X、Y、Z三个方向的力，对其进行合成就可以得到单个接触面的合力，对所有滚道采用APDL命令流的方式提取就可以得到所有滚道的载荷分布。

3.2 滚道寿命计算

轴承滚道内的载荷分布大小直接影响轴承的疲劳寿命[6]。当得到上一步计算的载荷后就可以开始计算轴承的寿命分布。结合ISO16281标准的轴承寿命计算方法，本文的计算过程如下：

(1) 求当量滚动体负荷。如图2所示，沟道1和沟道6形成接触对1，沟道2和沟道5形成接触对2，沟道3和沟道8形成接触对3，沟道4和沟道7形成接触对4，则接触对编号n=1,2,3,4。旋转套圈对应的接触位置的当量滚动体负荷Qevn计算公式为：

(1)

其中：Ψ为滚子方位角；QnΨ为从有限元模型中提取出来的滚动体上的载荷分布；Z为滚子个数。

静止套圈对应的接触位置的当量滚动体负荷Qeun计算公式为：

(2)

(2) 求内、外滚道的基本额定滚动体负荷Qci和Qce：

(3)

(4)

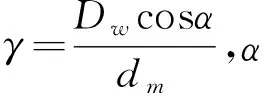
(3) 计算相对负荷旋转套圈滚道的额定寿命L10evn：

(5)

(4) 计算相对负荷静止套圈滚道的额定寿命L10eun：

(6)

(5) 每个接触对的额定寿命Ln计算公式为：

(7)

(6) 由式(7)可计算出每个接触对的额定寿命，即L1、L2、L3、L4，则轴承总的寿命计算公式为：

L10=min[L1,L2,L3,L4].

(8)

此寿命评估方法是以承受载荷最大的一对滚道的寿命作为整个轴承的寿命，以往的寿命评估方法过于保守，导致风机的成本过高。此方法已在各大轴承厂商中得到广泛的应用，同时也在实际风场的运行中得到验证。

4 实例计算

本变桨轴承承受的轴向力为345.4 kN，径向力为475.1 kN，合弯矩M=7 218.7 kN·m。将此载荷加载到建立的有限元模型中进行计算，得到的滚动体承受的最大赫兹接触应力如图7所示，轴承内外圈的变形云图如图8所示。通过工程算法计算出滚动体承受的最大载荷为104 kN，滚动体载荷分布如图9所示，而在ANSYS中进行后处理可以提取变桨轴承每个滚道承受的载荷如图10所示。对比图9和图10可以看出：两者之间的受载趋势一样，但是每个滚动体承受的最大载荷不一样，这是由于轴承内外圈的变形改变了每个滚动体上承受载荷的分布规律，考虑套圈的变形以后，最大滚动体承受的载荷会分配到其他的滚动体上。

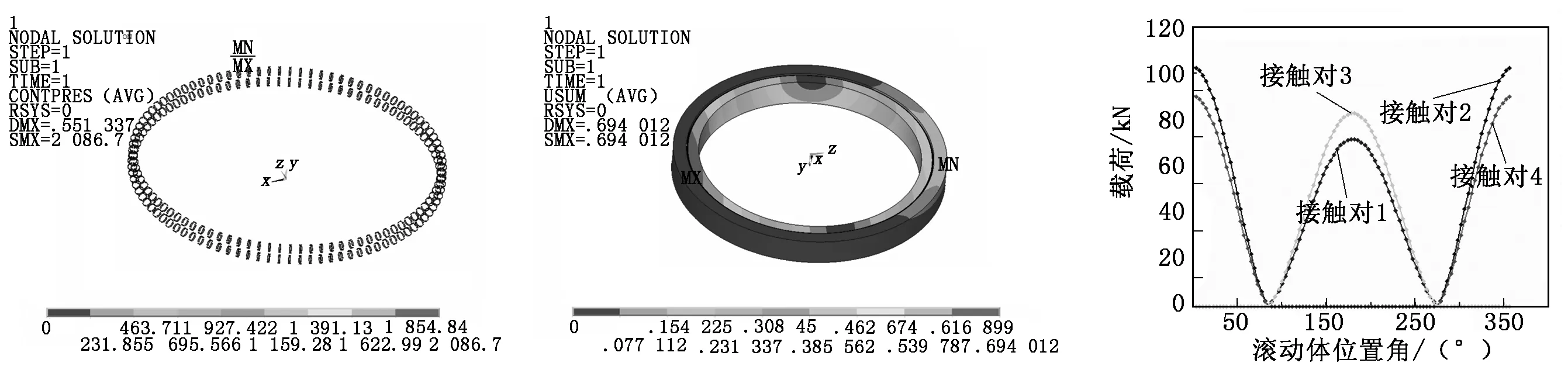
图7 滚动体赫兹接触应力图8 轴承内外圈变形云图 图9 工程算法得到的滚道载荷分布

图10 本文算法得到的滚道载荷分布

完全采用工程算法计算得到的滚子寿命为151 171转，采用本文的计算方法计算得到的滚子寿命为200 404转。由此可以看出：采用有限元方法计算出的轴承寿命更高。这是由于相比工程算法，在有限元算法中更多的滚动体分担载荷，降低了每个滚动体承受的载荷，考虑套圈的柔性更加符合实际的工程应用。

5 结论

变桨轴承滚动体载荷的分布大小决定着轴承寿命的多少，通过本文的方法可以准确计算出每个滚动体承受的载荷。由于本方法考虑了套圈和滚道的变形会导致更多的滚动体承受载荷，因此本方法比工程算法更加符合实际。本方法建立的模型可以求解任意载荷下轴承的受力和赫兹接触应力，省略了重复建模的麻烦，而且可以根据有限元模型提取出来的载荷直接计算轴承的寿命，从而把有限元方法和工程算法很好地结合起来，为轴承实际应用提供了新的方法，为轴承的研发提供了依据，为设计的改进提供了支撑，还可以用于轴承的刚度校核。

参考文献：

[1] 陈龙，杜宏武，武建柯.风力发电机用轴承简述[J].轴承，2008(12):45-50.

[2] 芮晓明，柳亦兵，马志勇.风力发电机组设计[M].北京：机械工业出版社，2010.

[3] 邓四二,贾群义,王燕霜.滚动轴承设计原理[M].北京：中国标准出版社,2008.

[4] 李云峰，刘彩霞，陈红涛.双排四点接触球转盘轴承的有限元分析[J].哈尔滨轴承，2015(2)：3-6.

[5] 郑辉，苪晓明，黄浙.风电机组变桨轴承变形研究与有限元分析[J].中国电力，2017,50(3):143-146.