基于改进AHP-灰色关联度法高速公路改扩建方案优选研究

安平和，苏兴矩，吴 强

(1.长安大学 公路学院，陕西 西安 710064;2.福建厦蓉高速公路漳龙段扩建工程有限公司，福建 厦门 364000)

随着经济的发展，高速公路的交通压力越来越大[1-2].中国早期建设的高速公路所能容纳的交通量较低，影响了高速公路“安全、经济、快速”的运输作用，亟待对老路进行加宽改造[3-6].赵梅龙，陈振伟等[7]采用AHP法进行了山区高速公路方案比选，但对于造价等已定量的评价指标(如造价等)依旧采用9度评价法将其评价指标得分转换为“权重”来进行比较，这是将已量化指标模糊化.火明彩[8]将灰色关联度与TOPSIS法相结合进行铁路选线比较，此方法适合于3种及以上备选方案.当只有两种方案时，只能得出2种方案孰优孰劣，但无法得出优劣程度.刘秀英，赵明登等[9]将AHP法与灰色关联度法首次进行结合，但依然将AHP法用于求备选方案的评价指标得分，没有解决指标主观评价过多的问题.本文用AHP法求出指标层的权重，将灰色关联度法直接用在求比选方案评价指标值上，减少了方案指标比选的主观性.

1 改进AHP-灰色关联度法

采用AHP-灰色关联度法进行多目标方案优选，步骤如下：

(1)建立方案比选层次模型

一般实际方案比选问题可分为3个层级[10]，即目标层(最终需要选定的方案)、准则层(各评价指标，可能为多层)和方案层，同一层级的因素对上层因素有影响，同时又支配下层因素.

(2)计算准则层指标权重

将准则层内同层指标进行成对比较来确定其权重，比较采用5人以上奇数数量专家打分来决策，将专家所打出的分数的平均数按下式建立比较矩阵[11]，如：对于目标层A建立比较矩阵A=(bij)n×n，其中bij为准则层内指标Bi相比于Bj的重要程度，采用9度评价法[12]，当bij的值为1、5、9时，因素i比因素j极端次要、一样重要、极端重要，当bij的值为1～9中其他数时，重要程度线性内插.

然后计算准则层权重W=(w1，w2，…，wn)，其中

(1)

(3)构建决策矩阵

多指标评价问题的方案集合为M=(M1,M2,M3,...,Mm),评价指标集合(如造价、工程难易程度)为N=(N1,N2,N3,...,Nn)[13],方案Mi对应指标Ni的评价值记为xij，则形成决策矩阵X为

(2)

(4)决策标准化矩阵

由于各评价值的数量级和量纲不同，故需要消除数量级和量纲之间的差异，这就需要对上面的决策矩阵进行无量纲化处理，构建标准化矩阵C=(cij)m×n，处理过程可按下式进行：

对于效益型指标(越大越优型指标)

(3)

对于成本型指标(越小越优型指标)：

(4)

组成标准化矩阵

(5)

选取参考序列c0={c0kk=1,2,...,n}，其中c0为每个评价指标最理想值[11].

(5)确定灰色关联系数

设Δi(k)=c0k-cik，则灰色关联系数为

(6)

其中，ρ为分辨系数，其主要目的是减少由于绝对差过大而失真的影响，通常ρ的取值范围为 0～1，本文取 0.5[14-15].所得到的灰色关联系数矩阵为：

(7)

(6)计算各方案优劣排名

各方案总得分为该方案所对应的各评价指标的灰色关联度乘以各指标对应的权重值，然后求和.

(8)

2 工程概况

厦蓉线扩容工程起于漳州天宝枢纽互通，终于龙长高速公路上杭蛟洋下道湖枢纽互通，全长124km.项目改扩建采用老路扩建、新建复线等方案.

其中排口至京源口段扩建工程考虑到龙门枢纽互通、龙岩西互通、考塘滑坡、京源口采空区、赣龙铁路、赣龙铁路扩能工程等路线制约因素影响对排口至京源口路段路线方案进行深化，共布设K线、E线等2个方案，并进行方案综合比选，如图2所示.

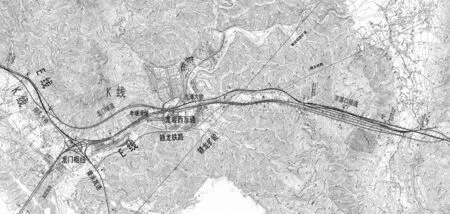
图1 排头至京源口段路线方案(K、E方案)比较示意图Fig.1 Comparison diagram of route scheme (K, E) from Paikou to Jingyuankou

(1)K线方案(K120+100～K133+045)

K线起于排头隧道出口(ZK120+100)，而后路线右线设排头特大桥(1 237 m)穿排头村，设赤水大桥上跨莆永高速.此后路线采用新建双向复线的方式沿莆永高速西侧布设，绕过龙门枢纽互通后，设龙门隧道(1 323 m)后抵龙潭村，而后K线上行线跨龙岩西互通匝道和龙长路主线后沿原龙长线北侧布线，下穿赣龙铁路扩能和赣龙铁路后与原龙长线连接，利用原龙长线作为扩容后厦蓉线上行线.K线下行线自龙潭村设龙潭特大桥上跨龙岩西互通，而后下行线上跨赣龙铁路扩能隧道和赣龙铁路隧道后新建京源口隧道并设置京源口特大桥跨现有龙长线后抵何家陂.K线沿线地层岩性主要为侏罗系象牙群粉砂岩，构造较发育，未发现对线路影响较大的滑坡、泥石流、崩塌、地裂等不良地质作用，工程地质条件较好.

(2)E线方案(K120+100～K132+950)

E线方案起于排头村(EZK120+100)，起点与排头隧道出口相接，路线对莆永高速进行双侧拼宽，利用原龙门枢纽互通后路线继续沿龙长高速进行拓宽，在龙岩西互通处新建下行线并利用原龙长线作为上行线.上行线(利用原龙长高速)下穿赣龙铁路和赣龙铁路扩能工程后经赖坑村穿京源口隧道，而后设置京源口特大桥抵何家坡.新建的下行线自龙岩西互通往西，设置龙潭特大桥经龙潭村，而后路线上跨赣龙铁路扩能隧道和赣龙铁路隧道后新建京源口隧道和京源口特大桥跨现有龙长线后抵何家坡.同时需对现有龙门枢纽互通及龙岩西互通进行改造.E线沿线地层岩性主要为侏罗系象牙群粉砂岩，不利条件是龙长高速考塘村附近存在古滑坡一处.

3 基于AHP-灰色关联度法方案优选

(1)建立方案比选层次模型

针对本段路线选择，方案集内共有2种方案，指标层则分为2层，第1层内分为“经济，技术，环境，社会”这4个大方面.在每一个大的评价指标下再细致划分，详细划分内容如下.

图2 方案比选层次模型Fig.2 Scheme selection hierarchy model

(2)计算准则层指标权重

按照层次分析法(AHP)中9度评价法进行评价，求出第1、第2指标层的权重向量，见表1-表5.

表1 评价指标权重Tab.1 Evaluation index weight

权重向量WA=(0.296,0.248,0.179,0.278)

表2 经济评价指标权重Tab.2 Economical evaluation index weight

权重向量WB1=(0.392,0.318,0.289)

表3 技术评价指标权重Tab.3 Technical evaluation index weight

权重向量WB2=(0.283,0.241,0.223,0.252)

表4 环境评价指标权重Tab.4 Environmental evaluation index weight

权重向量WB3=(0.319,0.334,0.347)

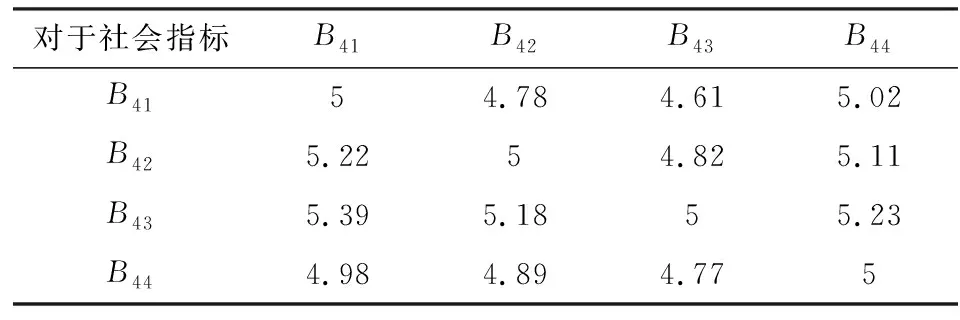
表5 社会评价指标权重Tab.5 Social evaluation index weight

权重向量WB4=(0.243,0.252,0.26,0.246)

统一准则层权重向量：将准则层第二层的权重向量与其对应的准则层第一次的权重向量相乘.

W=(b11，b12，b13，b21，b22，b23，b24，b31，b32，b33，b41，b42，b43，b44)

W=(0.116,0.094,0.085,0.073,0.059,0.055,0.062,0.057,0.059,0.062,0.067,0.070,0.072,0.068)

(3)量化方案评价值

在各评价指标值中，由于在线路比选时无法对其进行直接量化处理.通过模糊数学将这些定性指标转化为定量指标.本文对定性指标值采用模糊数学方法中的5级划分法进行赋值，即优、良、中、差、劣 5 个等级，相应的量化值分别为0.9,0.7,0.5,0.3,0.1.采用专家打分所计算的均值，各比选方案评价指标值见表6.

表6 比选方案评价指标值Tab.6 Evaluation index value of comparison scheme

(4)根据方案评价值建立决策矩阵

此时便已完成AHP法对权重的处理，接下来针对各评价指标值进行灰色关联度处理，由式(2)得出决策矩阵如下

(5)决策标准化矩阵

通过式(3)-式(5)将上面的矩阵计算得到决策标准化矩阵如下

(6)灰色关联系数矩阵

通过式(6)、式(7)将上面的标准化矩阵计算得到灰色关联系数矩阵

(7)2种方案总得分

通过式(8)整理求得用AHP-灰色关联度法得到的2种方案的总得分

P1=0.884，P2=0.792

结合上述方法得出的评分，K线方案赤水至龙潭段采用主线标准，通行能力较强，且对龙门枢纽及龙长高速干扰小，路线避开了考塘古滑坡，降低了施工风险.因此在初步设计阶段将K线方案作为该段路线的推荐贯通方案.

4 结束语

(1)层次分析法(AHP)中有较多的模糊数，若仅将AHP用于复杂方案比选中则容易造成结果偏向主观，而灰色关联度法在复杂方案比选中则不容易确定准则层的指标权重.本文将两种方法有机结合起来，即可以有效求得准则层中各评价指标的权重，也可以客观的求得备选方案中各评价指标值与最佳指标值的灰色关联度，以求得最佳方案.

(2)采用本文所提出的改进AHP-层次分析法进行方案优选，可以有效兼顾改扩建项目中成本、质量、工程进度、环境、土地征收、新结构对久结构影响、交通组织疏导等因素.在实际使用与操作上本方法简洁、有效，具有一定工程推广价值.

[1]蒋春阳. 高速公路改扩建工程方案评价指标体系研究[J]. 交通工程,2012(19):83-85.

[2]张丰焰, 周伟, 王元庆,等. 高速公路改扩建工程交通组织设计探讨[J].公路，2006(1):109-113.

[3]岳军委. 高速公路改扩建工程设计方法探讨 [J]. 中外公路，2015,35(6)：343-346.

[4]王晓，杨少伟. 高速公路改扩建工程交通组织方案优化设计[J]. 西南大学学报(自然科学版),2011(9): 146-151.

[5]韦勇球,赵利苹,袁春建，等. 高速公路改扩建交通组织仿真[J]. 长安大学学报(自然科学版)，2012(4)：38-43.

[6]马晓宁,王选仓,张涛. 高速公路改扩建条件评价体系研究[J]. 公路交通科技，2016(4)：52-58.

[7]赵梅龙，陈振伟. 基于层次分析法的山区高速公路路线方案比选研究[J]. 公路交通科技，2009(7):94-97.

[8]火明彩. 基于灰色关联改进的TOPSIS法在铁路线路方案综合评价中的应用 [D]. 兰州：兰州交通大学，2015.

[9]刘秀英，赵明登. 一种基于AHP-GRAP的山区高速公路路线方案优选方法[J].武汉大学学报(工学版)，2012(3)：356-360.

[10]赵保卿，李娜. 基于层次分析法的内部审计外包内容决策研究[J]. 审计与经济研究，2013(1):37-45.

[11]郭廷泰，韩晓虎，安平和，等. 基于FAHP法钢箱梁斜拉桥主梁施工方案比选[J]. 沈阳大学学报(自然科学版)，2016(3)：237-243.

[12]张霖波,冯长林,刘志强. 公路路线方案比选的模糊综合评价法[J]. 武汉理工大学学报(信息与管理工程版)，2009(2):347-350.

[13]李秀红. 基于灰色关联度的多目标决策模型与应用[J]. 山东大学学报(理学版)，2007 (12)：33-36,41.

[14]武新宇,范祥莉,程春田,等. 基于灰色关联度与理想点法的梯级水电站多目标优化调度方法[J]. 水利学报，2012(4)：422-428.

[15]韩晓，何明，李金林，等. 基于灰色关联度的科研项目风险评价方法[J]. 北京理工大学学报，2002 (6):778-781.