简解一类“恒成立”高考题
甘志国
(北京丰台二中 100071)
定理(1)若函数f(x)在x=a处可导,且x∈[a,b)时f(x)≤(≥)f(a)恒成立,则f′(a)≤(≥)0.
(2)若函数f(x)在x=b处可导,且x∈(a,b]时f(x)≤(≥)f(b)恒成立,则f′(b)≥(≤)0.
初步感知若f(x)≤f(a)(a≤x≤b),所以函数f(x)在x=a处右侧附近的图象是减函数.又函数f(x)在x=a处可导,所以f′(a)≤0.
同理,可得其他结论也成立.
严格证明若f(x)≤f(a)(a≤x≤b),由函数f(x)在x=a处可导及导数的定义,得
同理,可证得其他结论也成立.
例1 (1)(2006年高考全国卷Ⅱ)设函数f(x)=(x+1)ln(x+1).若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
(2)(2014年高考陕西卷)设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.若f(x)≥ag(x)恒成立,求实数a的取值范围.
解(1)设g(x)=f(x)-ax(x≥0),得g(x)≥g(0)(x≥0).
由定理(1)得g′(0)≥0,即a≤1.
由导数易证f(x)≥x≥ax(x≥0),所以所求实数a的取值范围是(-∞,1].
(2)可得题设即“(x+1)ln(x+1)≥ax(x≥0)恒成立”.由(1)知,所求答案也为(-∞,1].
例2 (2007年高考全国卷Ⅰ)设函数f(x)=ex-e-x,若对所有的x≥0,都有f(x)≥ax,求实数a的取值范围.
解同上可求得答案为(-∞,2].
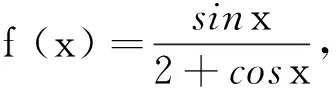


当x≥π且sinx≤0时,欲证成立.


例4 (2010年高考新课标全国)设函数f(x)=x(ex-1)-ax2,若当x≥0时,都有f(x)≥0,求a的取值范围.
解题设即f(x)≥0(x>0),也即ex-1-ax>0(x>0),还即ex-1-ax>0(x≥0).
用以上方法可求得答案为(-∞,1].
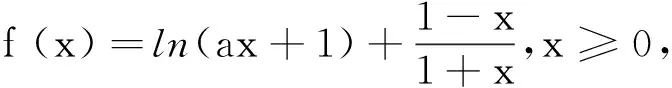
解设g(x)=f(x)-f(0)(x≥0),得题设即g(x)≥g(0)(x≥0).由定理(1)得g′(0)≥0,即a≥2.
当a=2且x≥0时,还可证g(x)≥g(0)(x≥0),即证(1+z)ln(2x+1)-2x≥0(x≥0).
设h(x)=(1+x)ln(2x+1)-2x(x≥0),得(2x+1)h′(x)=(2x+1)ln(2x+1)-2x(x≥0).
设t(x)=(2x+1)ln(2x+1)-2x(x≥0),得t′(x)=2ln(2x+1)≥0(x≥0),所以t(x)是增函数,得t(x)≥t(0)(x≥0),h′(x)≥0(x≥0),即h(x)是增函数,所以h(x)≥h(0)=0(x≥0),得欲证成立.所以当a≥2时,g(x)≥g(0)(x≥0).得所求a的取值范围是[2,+∞).
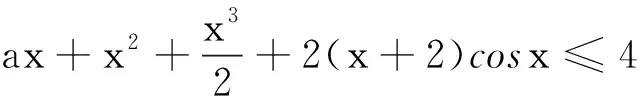

当a≤-3且0≤x≤1时,还可得:
得所求实数a的取值范围是(-∞,-2].
例7 (2017年高考全国)设函数f(x)=(1-x2)ex.
(1)讨论f(x)的单调性;
(2)当x≥0时,f(x)≤ax+1,求a的取值范围.
解(1)略.(2)设g(x)=ex(x2-1)+ax+1(x≥0),可得g′(x)=ex(x2+2x-1)+a(x≥0).
可得题设即g(x)≥g(0)(x≥0)恒成立,由定理1可得g′(0)=a-1≥0,a≥1.
设h(x)=ex(x-1)+1(x≥0),可得h′(x)=xex≥0(x≥0),h(x)是增函数,得h(x)≥h(0)=0(x≥0).
所以当a≥1时,g(x)≥ex(x-1)(x+1)+1(x+1)≥0(x≥0).
综上所述,可得所求a的取值范围是[1,+∞).
参考文献:
[1]刘绍学.普通高中课程标准试验教科书·数学选修2 -3(必修A版)[M].北京:人民教育出版社,2007.

