对2014年高考湖北卷理科第9题的探究

刘彦永

(东北师范大学附属中学 130021)

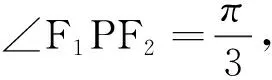
一、试题分析

本题属于传统题，考查了椭圆和双曲线的定义和性质、正弦定理和余弦定理等知识点.以圆锥曲线为载体，考查了数形结合思想、等价转化能力和函数方程及不等式思想.

二、解法探究

本题解法很多，不同的解法体现不同的思维层次和思考角度，这里要求考生要有一种勇于探索、敢于实践的精神.

记|PF1|=m>0，|PF2|=n>0，|F1F2|=2c，椭圆和双曲线的离心率分别为e1和e2.不妨设m>n，则

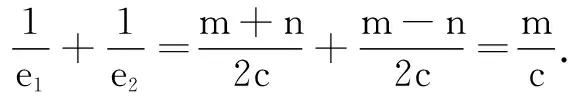
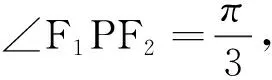
思路2 在△F1PF2中由余弦定理得|F1F2|2=

|PF1|2+|PF2|2-2|PF1|·|PF2|cos∠F1PF2,即(2c)2=m2+n2-2mncos60°=m2+n2-mn.

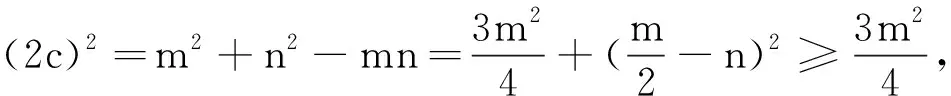
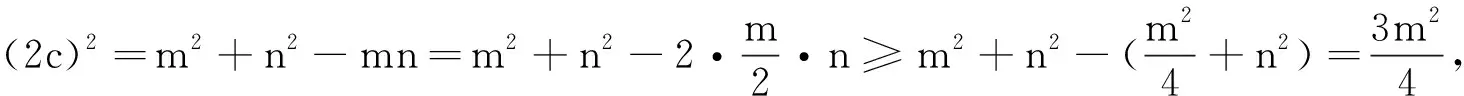
思路3 在△F1PF2中,由余弦定理得：

|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos∠F1PF2=(|PF1|+|PF2|)2-3|PF1|·|PF2|，

①

|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos∠F1PF2=(|PF1|-|PF2|)2+|PF1|·|PF2|。

②

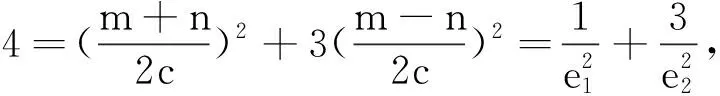
注此结论也可由如下两种方法得到.

(1)利用椭圆和双曲线的焦点三角形面积公式

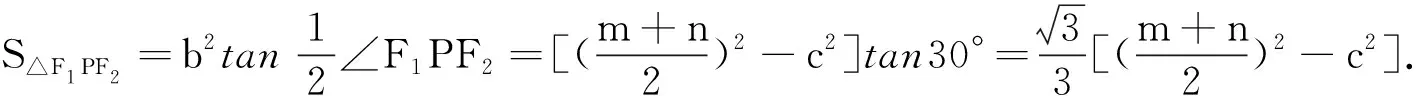
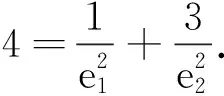
(2)利用待定系数法

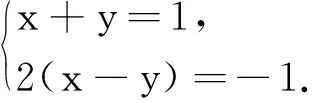
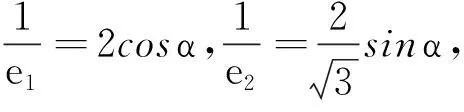
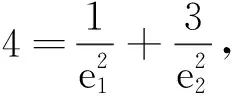
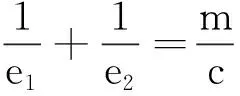
参考文献：

[1]人民教育出版社,课程教材研究所数学课程教材研究开发中心.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.