数学归纳法的应用

樊庆林

(广东省韶关市田家炳中学 512000)

高中数学体系是对初中数学体系的进一步发展和完善，是学生由具体运算向形式运算过渡的重要时期，旨在提升学生的逻辑思维能力和利用数学知识解决实际问题的能力.在我们高中数学学习和解题中，数学归纳法是一种很常见的方法，其通过对简单数值代入计算结果的总结，推导出通用的计算公式，是对数学规律性问题解决的一种有效工具.在多年的高中数学实践教学中，笔者对数学归纳法的应用有一些了解，因此笔者对数学归纳法做出以下简要分析，对于实践教学中发现数学归纳法运用的不足之处，还要不断加以改进和完善.

一、数学归纳法的简单介绍

数学归纳法是数学中很重要的分析解题方法，本质上是通过对简单数值的计算推广到一般的演绎规则，从小规模成立的假设推导出较大规模情形成立的一种方法，以这种类比的思想对数学知识进行一种逻辑上推断证明的方法.对一般的数学归纳法有以下基本的步骤：

(1)当n=1时，这个命题是正确的.

(2)然后我们假设当n=k时，这个命题还是正确的，进而推断当n=k+1时，这个命题也是正确的，从而推断出命题在任意数值代入计算后结论恒成立.

二、数学归纳法的应用

1.数学归纳法在几何问题中的应用

高中几何问题向来是比较难的问题，在解题中需要学生由较强的空间想象能力和思维推导能力.在几何方面无论是计算问题还是证明问题都使得很多同学在解答的时候容易思维混乱、逻辑不清晰，很容易就把自己绕进去得不出正确答案.根据笔者多年课堂上的教学经验，做以下举例对此作出分析.

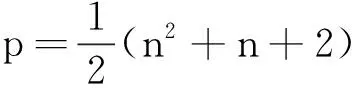
对此问题下面我们根据数学归纳法进行证明.

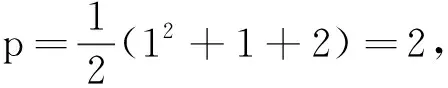
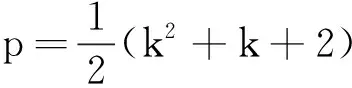
2.数学归纳法在排列组合中的应用

排列组合是我们高中数学比较重要的一块内容，其学习目的是可以让学生拥有对一些问题整体把握的能力，即以“上帝”的视角解决状态空间的问题.但学生在排列组合的相关知识学习中有很大难度，并且教师在讲授的时候一般需要很长时间，为有效提高教学效率，我根据排列组合知识具有很强规律性的性质特点将数学归纳法灵活应用于教学中，促进学生对排列数公式、组合数公式、自然数n的阶乘公式，二项式定理等重要公式的理解和掌握.

3.数学归纳法在解不等式的应用

其实，在我们的高考数学复习的时候，会遇到各种题目类型，数学归纳法的解题作为一个专题都不为过.一般情况下，数学中不等式证明题的时候往往要用到放大或缩小的办法，有了放大和缩小一般很轻易就能得到答案.而关于正整数n的不等式，常可考虑用数学归纳法来证明.

4.数学归纳法在解决整除性问题中的应用

通过对整除性问题的学习可以让学生对数学数字进行更灵活的把握，对其产生更敏锐认知，而具体数值的整除问题中学生可以通过公式计算出结果，但高中数学更加注重形算能力的培养，要求学生能对非具体计算做出准确运算,下面将数学归纳法在整除性问题的解决应用中作出分析.

例2 设n是自然数，求证32n+2+26n+1能被11整除.

证明(1)当n=0时，32+21=11，能被11整除，命题成立.

(2)假设n=k(k≥0,k∈N)时，命题成立，即

11|32k+2+26k+1.

那么当n=k+1时32( k + 1)+2+ 26( k + 1)+1==9×32k+2+64×26k+1=9(32k+2+26k+1)+55×26k+1.

由假设知11|9(32k+2+26k+1),

又显然有11|(55×26k+1),从而知11|(32(k+1)+2+26(k+1)+1),即当n=k+1时命题也成立.因此对任意自然数n，命题都成立.

三、思考与展望

现在数学归纳法在很多类型的题目中都有应用，其不仅能帮助学生拓展解题思路优化学习方法，还能培养学生的发散思维能力，因此在教学中我们也很注重这种解题方法.总之，数学归纳法的确是一种很重要的解题方法，在历年高考真题中我们就能发现它的广泛应用，这部分内容不仅是我们教学的一个重点也是难点，我们也在不断地探索中对其进行优化和改善，争取实现教学水平的不断提高.

参考文献：

[1]乌仁.浅谈数学归纳法的两个步骤及其应用[J].赤峰学院学报，2007(6).

[2]张黎民.数学归纳法的应用与技巧[J].青海师范大学民族师范学院学报，2001(1).