多种方法解一道高考向量平行问题
苏保明
(云南省红河州蒙自市蒙自一中新校区 661100)
在平面向量中有一类关于两个向量平行(或共线)的问题,常常出现在高考真题中,其题目简单朴实,解题思路却灵活多样,求解过程妙趣横生,能更好地考查学生综合应用数学知识解决具体问题的能力,本文列举一道2016年的高考题介绍一题多解.
题目(2016年高考新课标Ⅱ卷文科数学)已知向量a=(m,4),b=(3,-2)且a∥b,则m=________.
这是一道以向量知识为背景的选择题,虽然试题内容朴实、形式平和,但解题方法灵活巧妙.如果我们略加思考,进行追本溯源,那么此高考题的根源来于“普通高中课程标准实验教科书数学必修4(人教版)”中的三个例(习)题:
(1)P98例6:已知a=(4,2),b=(6,y),且a∥b,求y.
(2)P101习题2.3A组5:n为何值时,a=(2,3)与b=(x,-6)共线?
(3)P118复习参考题A组8:n为何值时,向量a=(n,1)与b=(4,n)共线且方向相同?
经过笔者的认真思考和研究,给出上述高考题的几种解法.
方法一:利用向量平行的坐标公式
思路点拨利用向量平行的坐标公式:若a=(x1,y1),b=(x2,y2)(b≠0),则a∥b的充要条件是x1y2-x2y1=0.
解法1 因为a=(m,4),b=(3,-2) 且a∥b,
所以(-2)×m-3×4=0,所以m=-6.故填:-6.
评注利用向量平行的坐标公式解决向量平行问题,是最基本的常规解法,属于通性通法.此法通俗易懂,务必熟练掌握.
方法二:利用向量共线定理
思路点拨利用向量共线定理:向量a与b(b≠0)共线,当且仅当有唯一实数λ,使a=λb.
解法2 因为a∥b,且b≠0,
所以当且仅当存在实数λ,使a=λb.

故填:-6.
评注向量共线定理是解决一切向量共线问题的最有效的方法,对于较为复杂的问题也不失为一种好方法,只有掌握其本质,才能运用自如.
方法三:利用直线的斜率
思路点拨如果同一平面内的三点共线,并且任意两点所在直线的斜率存在,那么任意两点所在直线的斜率相等.
解法3 设a和b的始点都是原点O(0,0),则a和b的终点分别是A(m,4),B(3,-2).
因为a∥b,且有公共始点O,所以直线OA与直线OB重合,
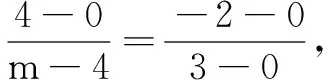
评注把向量平行问题转化为向量所在直线平行(或共线)问题,利用斜率相等解决向量平行问题,不失为一种灵活的解题方法.
方法四:利用点与直线的位置关系
思路点拨如果同一平面内的三点共线,那么任意两点所在直线经过第三点.
解法4 设a和b的始点都是原点O(0,0),则a和b的终点分别是A(m,4),B(3,-2).
因为a与b共线,且有公共始点O,所以点O、A、B三点共线.
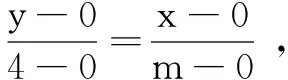
因为点B(3,-2)在直线OA上,

解得m=-6.故填:-6.
评注借用三点共线的特殊情形“任意两点所在直线经过第三点”这一结论,巧妙地与向量平行“牵手”求出m的值,从而进一步证实了向量平行问题与直线平行(或共线)问题的内在关系和紧密联系.
方法五:利用点到直线的距离
思路点拨如果同一平面内的三点共线,那么任意一点到另外两点所在直线的距离等于0.
解法5 设a和b的始点都是原点O(0,0),则a和b的终点分别是A(m,4),B(3,-2),
因为a与b共线,且有公共始点O,所以点O、A、B三点共线,
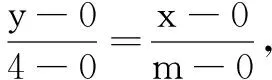
所以点B到直线OA的距离为
所以|12+2m|=0,解得m=-6.故填:-6.
评注借助三点共线的巧妙方法“任意一点到另外两点所在直线的距离等于0”,巧妙地与向量平行“联手” 求出m的值,此法需要同学们在平时的解题过程中加以分析、思考和归纳总结,解题时才能运用自如.
方法六:利用两直线重合的内在关系
思路点拨如果同一平面内的三点共线,那么任意两点所在直线的未知数的系数分别对应相等,且常数项对应相等.
解法6 设a和b的始点都是原点O(0,0),则a和b的终点分别是A(m,4),B(3,-2)
因为a与b共线,且有公共始点O,所以点O、A、B三点共线,
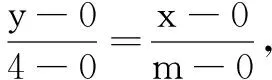
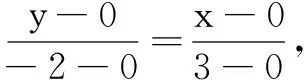
因为直线OA与直线OB重合,所以未知数x与y的系数分别相等,
所以-m=6,即m=-6.故填:-6.
评注借助两直线平行的内在关系“未知数x与y的系数分别相等,常数项对应相等”这一关系,巧妙地与向量平行“联姻” 求出m的值,此法灵活性较强,需要熟练掌握,才能巧妙运用.
参考文献:
[1]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.普通高中课程标准实验教科书(必修)数学4(A版)[M].北京:人民教育出版社,2014.

