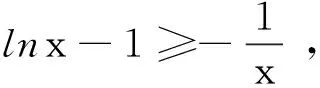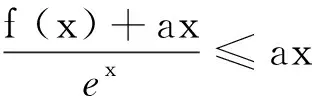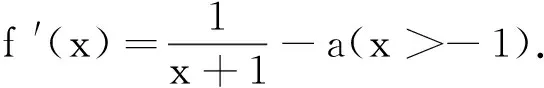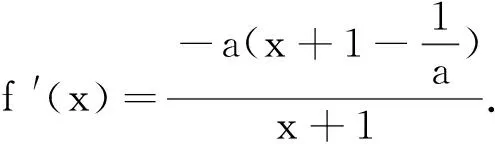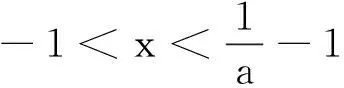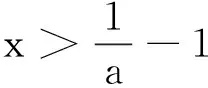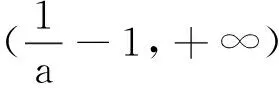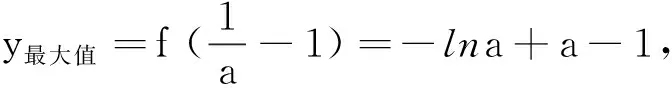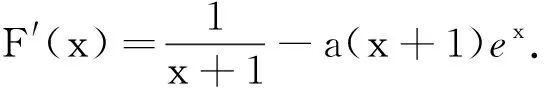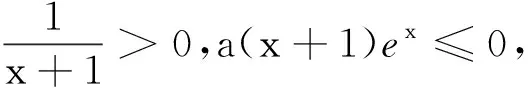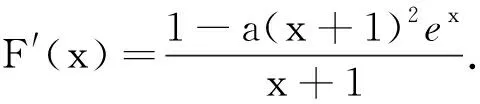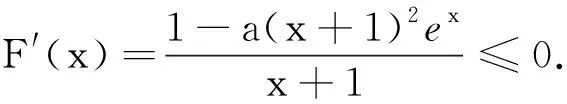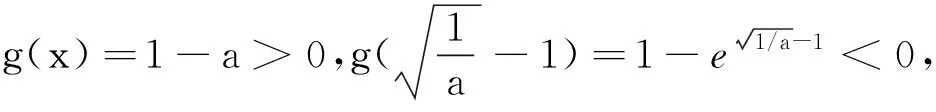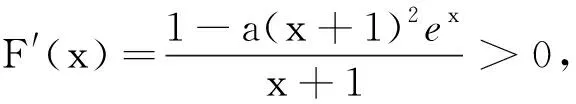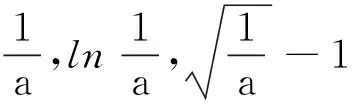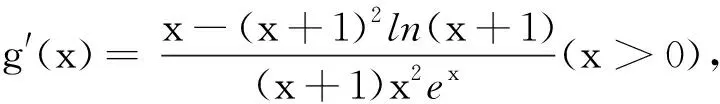例谈函数与导数中的分类讨论策略

卢云辉

(福建省厦门市松柏中学 361012)

我国著名数学家陈景润先生在《谈怎样学习数学》中提到,要做高质量的数学题目,要善于独立开展解题活动,对待问题的观点是要从正面、反面各个角度多想想,要善于找到它们之间的联系,总结出规律性的东西.本文对函数与导数问题中的分类讨论策略进行整理与归纳,便于读者参考与借鉴.

分类讨论实质是一种“化整为零，各个击破，再积零为整”的解题策略.解题步骤大致为:①确定分类标准,正确进行分类;②分类进行讨论,获取分类成果;③综合得出结论.

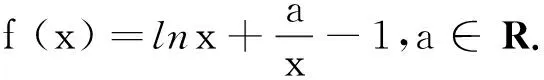
(1)若函数f(x)的最小值为0,求a的值;

(2)证明:.ex+(lnx-1)sinx>0.

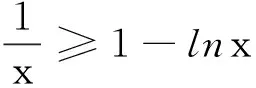
(2)当x>0时,ex>0,而(lnx-1),sinx有正有负.讨论sinx的正负分为0

点评当某一项正负值不能确定时可以采用分类讨论策略.如本题中当x>0时,ex>0而(lnx-1),sinx,有正有负,讨论sinx的正负分为0

例2 (2017年厦门市高二年第二学期质检理)已知函数f(x)=ln(x+1)-ax,a∈R.

(1) 讨论f(x) 的极值;

(其中e为自然对数的底数)

①当a≤0时，f′(x)>0，f(x)在(-1,+∞)上单调递增，无极值.

综上可得，当a≤0时，f(x)无极值；当a>0时,

f(x)有极大值-lna+a-1，无极小值.

记F(x)=ln(x+1)-axex(x≥0)，

只需F(x)max≤0.

所以F(x)在[0,+∞)上单调递减，故当x≥0时，F(x)≤F(0)=0，符合题意.

当0

所以g′(x)=-a(x+1)(x+3)ex<0，g(x) 在[0,+∞)上单调递减.

当0g(x0)=0，

分类讨论不仅是一种典型的逻辑方法,而且也是一种非常重要的数学思想,这是因为数学自身的概念、定理、公式、法则、性质等有不少都是分类规定或研究的.而数学解题作为一个思维过程,其最大的特点在于它是一个渐进的、曲折的过程.在解复杂问题过程中,我们需要套路,但又不能拘泥于套路.否则,套路可能遮蔽我们的眼睛,这就是数学解题的辩证法.

参考文献：

[1]刘文杰.高中数学复习课模式的探究:《函数与导数的应用》课堂教学设计案例[J].课程教育研究,2013(08).