基于冗余信息的STL模型快速切片算法*
钱 乘 李 震 江本赤
(安徽工程大学,安徽 芜湖 241000)
3D打印技术(3D Printing)理论上可以打印出任何模型,被认为第三次工业革命的代表性技术,其广泛运应于机械制造、医学领域、房屋建筑、汽车行业、电子行业等[1]。对大多数3D打印系统而言,理论模型首先被构建,根据用户对精度的需求设定参数将模型转换为STL文件,然后对STL模型进行切片处理。切片处理是3D打印系统中重要的一步,切片轮廓是生成刀具路径与逐层沉积的基础。STL模型将实体模型表面细分三角形来获得,丢失了其原有模型的拓扑信息。STL模型每个三角形面片的顶点至少被记录4次,从而带来额外的计算存储器占用和时间消耗;当物体表面的所需近似精度增加时,生成的STL文件的大小被大幅度增加,等等。这些造成了对STL模型切片算法效率较低。STL文件虽然存在数据冗余且无拓扑关系的缺陷,但是由于具有生成简单性、输出的广泛性、易于切片处理等优势,对STL模型切片算法的研究仍然是研究的主流[2]。
目前,研究人员已提出了多种对STL模型切片算法。定层厚切片是目前普遍使用的切片算法,主要有3种即基于面片拓扑关系的分层切片算法,基于模型几何特征的分类算法以及基于几何连续性的切片算法[3]。Zhang等人[4]利用三角形之间的拓扑关系进行切片的优化;王彦云等人[5]通过建立点表与面表快速实现拓扑信息重建。上述方法可以提高切片效率,但是拓扑关系的构建需要花费时间较长且占用内存大。Chakraborty等人[6]提出了三角形的精简排序,提高算法效率,王春香等人[7]提出了快速精简算法,直接提取只与切片面相交的三角形面片,提高分层效率,但是排序界限非常模糊,不能够避免三角形面片与分层平面位置无关的无效判断,且需要对杂乱无章的交线段进行排序;王素等人[8]提出了STL模型的分层邻接排序快速切片算法,朱君等人[9]建立STL模型的分层面新相交三角形面片表文件,提取模型的活性拓扑结构的方式,加快分层速度,但是在动态面片组合中,增减三角形操作,拓扑关系构建仍然耗时。对于自适应算法而言,Hayasi[10]、Sikder[11]等专家学者进行了深入的研究,自适应切片方法切片速度较慢,但是精度比较高。
考虑到对STL模型切片过程中存在的冗余信息,本文提出了一种基于冗余信息的STL模型快速切片算法。在分析STL模型信息的基础上,对于第i层切线平面,建立只与其相交的三角形集合,减少切平面与三角形相交判断次数;分析了STL三角形面片与切平面的位置情况,求出集合中各三角形与切平面的交点信息并记录交点存储形式,将坐标值重复的交点视为冗余信息并分析拓扑关系可能存在的两种情况,根据交点的冗余信息通过逐点识别与剔除以建立三角形之间的拓扑关系;依据拓扑关系获得有序点列依次连接,得到二维封闭轮廓。通过两个典型模型对该切片算法进行检验,表明该算法对STL模型进行切片处理有较好的效果。
1 STL模型的特点
1.1 STL模型的获取
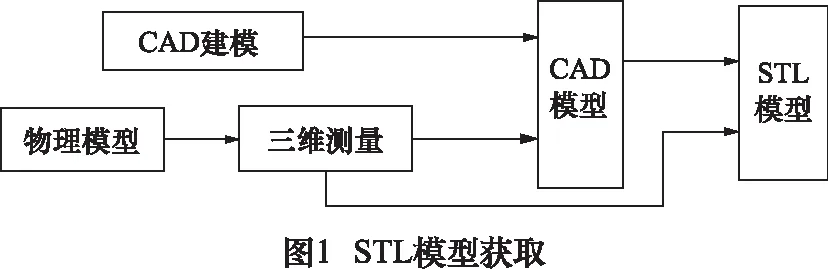
目前通常利用两种方法来生成三维模型即正向设计技术与逆向设计技术。前者利用三维CAD工具建立模型,例如:AutoCAD、UG、SolidWorks等等,利用计算机生成、处理、存储、输出三维空间模型。CAD物理模型确定了表面的方向性、形体内部材料的物理性能等参数、其几何和拓扑信息最为完善的模型[12]。后者即三维测量技术建立模型,其大致可以分为4个阶段:首先利用三坐标测量机(CMM)或者激光扫描仪来获取零件原形表面点的三维坐标(点云数据);其次对点云数据进行预处理,去除不可用的数据;然后从测量数据中提取零件原型的几何特征;最后进行零件CAD模型的重建[13]。
一般的CAD系统可直接转换成STL格式;也可以直接对点云模型进行三角网格重构,目前比较流行的方法Delaunay三角剖分,其对应关系如图1所示。
1.2 STL文件信息存储特点
STL(STereoLithographic)是由3D SYSTEM公司在1988年制定的一个接口协议[3]。STL文件由多个三角形面片定义组成,每个三角形面片的定义包括三角形3个顶点的坐标以及法向量。由于STL格式生成简单性、输出的广泛性、易于切片处理等优势,已然成为3D打印行业默认的标准文件格式。STL文件虽然简单易懂,仅仅记录了坐标信息和法向量信息,但是几何体之间的拓扑信息并没有表达,三角面片记录杂乱无章。
STL存在两种格式:文本(ASCII)格式与二进制(BINARY)。ASCII格式记录了每个字符和数字,具有可读性,直观性,方便进一步对数据进行处理。二进制STL格式更紧凑,其大小约为ASCII格式的STL文件大小的1/6,文件尺寸小、易于传输、对于数据处理更有效。STL文件文本与二进制结构分别如表1所示:

文本格式结构二进制格式结构solid filename //文件名称 UINT8[80] // 文件头facet normalnxnynz // 法向量坐标UINT32 // 三角面片数量outer loopforeachtriangle // 定义一个三角面片vertex x1y1z1 // 第一个顶点坐标REAL32[3] // 法向量矢量vertexx2y2z2 // 第二个顶点坐标REAL32[3] // 第一个顶点坐标vertexx3y3z3 // 第三个顶点坐标REAL32[3] // 第二个顶点坐标endloopREAL32[3] // 第二个顶点坐标endfacet //完成一个三角面片定义UINT16 // 文件属性… // 循环定义三角面片… // 循环定义三角面片endsolid// 文件定义结束end // 文件定义结束
2 基于冗余信息的STL模型切片算法
对于第i层切平面,建立只与该层切平面相交的三角形集合;分析了STL三角形面片与当前切平面的位置情况,求出集合中各三角形与切平面的交点信息;分析了拓扑关系一般与特殊的两种情况;利用冗余信息重建拓扑关系;然后依据拓扑关系得到有序点列,依次连接;最后得到二维封闭轮廓。
2.1 相交三角形集合的建立
在进行分层处理的过程中(z轴方向为分层方向),建立只与当前切平面相交的三角形集合,减少切平面与三角形的相交判断次数,提高整体切片效率。
2.1.1 预处理
在进行数据操作时,为减少数据的处理量,忽略法向量信息。法向量可由STL记录的3个顶点坐标获得,可以把法向量坐标看作冗余数据进行处理。对ASCII文件进行读入时法向量坐标应进行删除;并根据每个三角形三个顶点z坐标值升序排序。预处理操作步骤如下:
Step1:根据ASCII文件记录特点,1、5、9、…、4(n-1)+1行记录法向量坐标,将其对应的行数删除(n为三角形面片数)。
Step2:按照每个三角形3个顶点的z坐标进行升序排列。
Step3:将得到的排列后的顶点数据排成一行每行代表1个三角形,即:[(x1,y1,zmin)(x2,y2,zmid)(x3,y3,zmax)]。
Step4:将所得到的数据依据zmax以行为单位进行升序排列。
2.1.2 集合的建立
经过分析,与切平面zi无关的三角形有图2所示3种情况,三角形T1、T2、T3分别为每种情况的示例。根据2.1.1节中三角形顶点的记录方式,其删除条件分别为:zmax
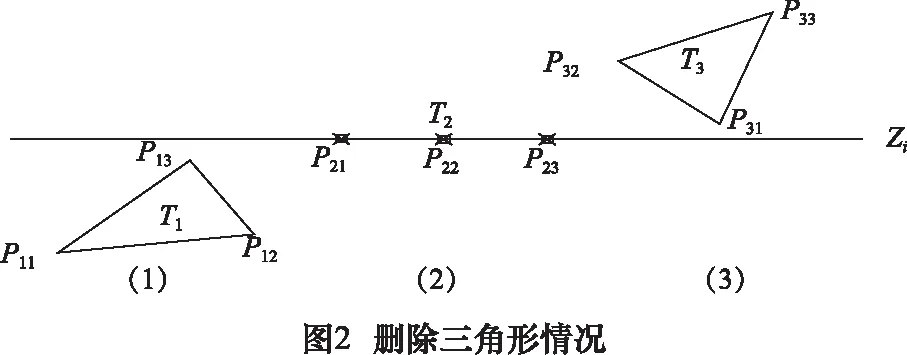
删除上述3种无关三角形,建立相交三角形集合步骤如下:
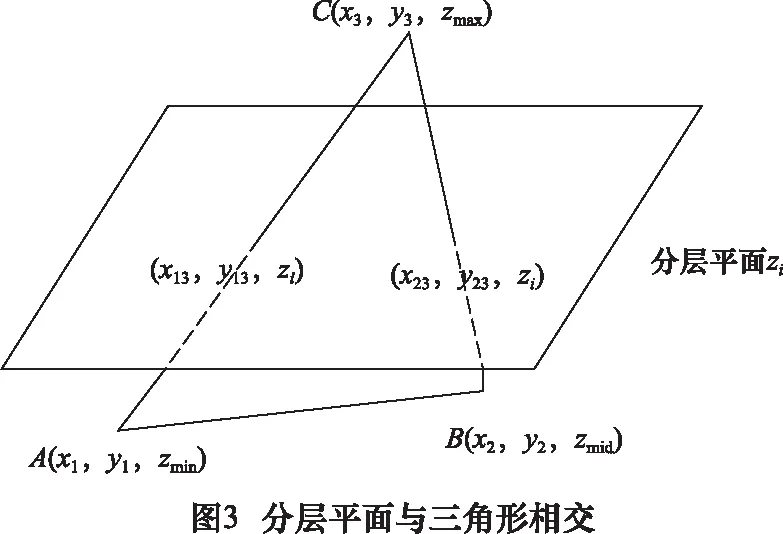
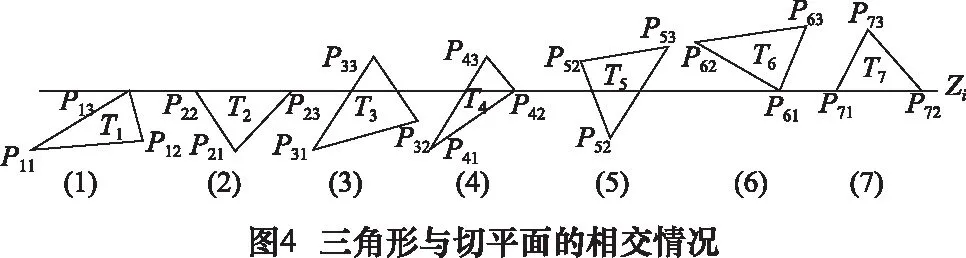
Step1:升序排序后的三角形顶点坐标zmax与切平面高度zi进行比较,判断zmax Step2:从三角形顶点数组中删除前p行向量与删除数组相同坐标的向量。 Step3:将得到的数组依照zmin以行为单位进行降序排列。 Step4:判断zmin>zi, 记录下最终行数q。 Step5:从排序后的数组中删除前q行向量。 经上述操作即得到只与当前切平面相交的三角形集合。 2.2.1 交点计算公式 分层切片是用一系列与XOY平面相平行的平面去截取STL模型。截面轮廓为分层平面与STL模型相交三角形所得交点依次连接起来的多边形。如图3所示,ΔABC为STL模型中任意三角形,分层平面高z=zi。 根据AC的直线方程可得到: (1) 可得: (2) 同理可得: (3) 2.2.2 三角形与切平面相交的情况分析 为简化相交判断条件,对相交三角形的z向坐标与分层高度zi进行差值处理,即:[(x1,y1,zmin-zi)(x2,y2,zmid-zi)(x3,y3,zmax-zi)],然后运用差值处理后的z向坐标与0进行比较,从而判断处于那种相交情况,应用2.2.1节中的交点计算公式计算交点。交点的记录对zi坐标进行忽略,仅仅记录交点x,y坐标,即:[(x13,y13)(x23,x23)],在绘制轮廓时对交点坐标进行循环赋zi值。经过分析集合中各三角形与切平面共有7种相交情况如图4所示。 三角形T1、T2、T3、…、T7分别为每种情况的示例,根据2.1.1节中三角形顶点的记录方式,判断三角形与切平面的相交处于何种情况的条件以及交点的记录方式依次为: (1)zmax-zi=0且zmid-zi<0,交点坐标记录:[(x3,y3)(x3,y3)]。 (2)zmax-zi=0且zmid-zi=0,交点记录:[(x2,y2)(x3,y3)]。 (3)(zmax-zi)×(zmid-zi)<0且(zmax-zi)×(zmin-zi)<0,交点记录:[(x13,y13)(x23,y23)]。 (4)(zmax-zi)×(zmin-zi)<0且zmid-zi=0,交点记录:[(x13,y13)(x2,y2)]。 (5)(zmax-zi)×(zmin-zi)<0且(zmid-zi)×(zmin-zi)<0。交点记录:[(x13,y13)(x12,y12)]。 (6)zmin-zi=0 且zmid-zi>0,交点记录:[(x1,y1)(x1,y1)]。 (7)zmin-zi=0 且zmid-zi=0,交点记录:[(x1,y1)(x2,y2)]。 对于获取的交点坐标,(1)与(6)、(2)与(7)、(3)与(5)、(4)分别存入独立的临时数组,以方便对影响拓扑关系的交点的处理。 根据STL模型连续三角形面片与切平面的相交情况,依据交点数组冗余信息重建的拓扑关系可以总体分为图5所示两种情况。图5a所示的一般拓扑关系根据重建之后的拓扑关系,获得的有序点列不会造成轮廓不封闭的现象。图5b所示的特殊拓扑关系在进行拓扑重建时将会受到三角形T2、T5、T7、T3或T6的影响,从而造成轮廓不封闭现象。可将影响拓扑关系重建的三角形分为两种情况即:两个顶点与切平面相交与三角形一个顶点与切平面相交。前者应对交点坐标进行去重操作,后者根据与相邻三角形的交点坐标重复的特征进行删除操作。两种情况余留下的交点坐标即为不影响拓扑关系重建的交点坐标。 2.3.1 交点坐标去重 将两个顶点与切平面相交的情况,视为情况1,进行去重操作。具体步骤如下: Step1:将此临时数组交点坐标以x进行升序排序,若x坐标值相同则以y坐标值进行升序排序,即:[(xmin,y1)(xmax,y2)]。 Step2:将数组的第一行坐标赋值给一个变量如变量a,并存入另一临时数组,并将此行坐标从临时数组中删除。 Step3:以变量a进行搜索该数组,若在临时数组中搜索到与之相同的坐标信息便将此行坐标从临时数组中删除。 Step4:判断临时数组是否为空,若数组为空搜索结束,变量a坐标所存入的另一临时数组代替原临时数据,变为情况1的交点数组,若不为空,重复上述Step2、Step3步骤。 2.3.2 交点坐标删除 三角形一个顶点与切平面相交的情况,视为情况2,根据相邻交点坐标重复进行删除操作。具体步骤如下: Step1:将此数组的具有相同坐标的行进行删除并保留一个,得到不重复交点数据组成的数组。 Step2:将得到的数组每一行的第一个交点坐标,与2.2.2节情况(4)的交点存入的临时数组和上述情况1的交点数组的交点坐标,进行比较。 Step3:若存在相同,记录下该行在此数组中的行数。 Step4:将此数组中被记录下的行数进行对应删除。 由于STL模型丢失了原物理模型之间的拓扑关系,三角形的记录杂乱无章,需要对其重建三角形之间的拓扑关系。由于STL模型三角形之间存在共边原则,切片过程中存在的交点冗余信息,基于此信息利用逐点识别与剔除的思想重建拓扑关系。如图6所示,三角形面片T1、T2根据STL文件规则共用一条边,T1与T2交点记录形式分别为[ab]、[cd],其中由于b与c坐标值相等,若以b坐标搜索整个交点数组进行三角形拓扑关系的构建,那么c坐标便为b坐标的重复交点,视为冗余信息。具体步骤如下: Step1:将交点数组的第一行赋值给一个变量如d,并存入有序数组并将此行坐标从整个交点数组中删除。 Step2:应用变量d的第二点坐标,进行整个交点数组的搜索,记录此时交点数组行数k1。 Step3:搜索到与第二点坐标相同的坐标,并将此行坐标以d第二点为第一点进行重新排列,并将排列后的此行坐标赋值给d与有序数组,并从交点数组中删除该行,记录下删除后的交点数组行数k2,k1=k1-1。 Step4:判断k1=k2是否成立,若相等则说明有序点列未形成一个封闭的截面轮廓,重复Step2、Step3;不相等说明在交点数组中己不存在该d的冗余信息,有序点列己形成一个封闭的截面轮廓。 Step5:判断交点数组是否为空,若为空,说明当前切片层内的其余封闭轮廓完全获得结束循环;不为空,说明该切片层内存在其余的封闭轮廓,重复上述Step1、Step2、Step3、Step4,直至为空。 拓扑关系重建完成后,需要从中获取有序点列依次进行连接,形成封闭的截面轮廓。对应关系如图7所示。三角形面片T1、T2、T3、…、Tk根据上述重建的拓扑关系可得到每个三角形交点有序排列,如:[ab]、[bc]、[cd]、…、[ja]。从中可以看出上述有序点列重复,需要获取单个有序坐标,即:[a]、[b]、[c]、…、[j]、[a],依次进行连接,形成封闭多边形。 具体步骤如下: Step1:初始坐标点插入有序数组最后一行,形成新的有序数组。获取有序数组的第一个交点坐标(有序数组的第一列与第二列元素,获得依次连接的交点坐标)。 Step2:对获取后的交点依次赋值zi,成为完整的三维坐标。 Step3:依次进行连接,得到二维截面轮廓。 为了检验上述算法的可行性与可靠性,给出了图8所示两个实例进行验证。图9与图10分别为奖杯与饰品的模型切片效果图,图9a与图10a分别为STL切片模型,图9b与图10b分别为其中某层切片轮廓。可见,该算法对STL模型的切片处理有较好的效果。 (1)建立只与当前切平面相交三角形的集合,可减少切平面与三角形相交判断次数,从而提高了切片效率。 (2)分析了特殊拓扑关系的存在情况,对于影响拓扑关系的两种情况的交点,依据各自特点进行删除操作,保证有序点列形成封闭截面轮廓,不受无关点列的影响。 (3)基于逐点识别与剔除思想的拓扑关系重建,有效减少了遍历交点数组的次数,提高了切片效率。 [1]李晓丽, 马健雄,李萍,等.打印技术及应用趋势[J].自动化仪表, 2014, 35(1):1-5. [2]韩霞, 杨恩源.快速成型技术与应用[M].北京:机械工业出版社, 2012. [3]黄丽.基于STL模型分层算法研究与软件实现[D].泰安:山东农业大学,2016. [4] Zhengyan Zhang, Sanjay Joshi. An improved slicing algorithm with efficient contour construction using STL files[J]. Int J Adv Manuf Technol, 2015, 80(5):1347-1362. [5]王彦云, 陈鸿, 谢明师,等.基于哈希表的STL格式文件拓扑重建的算法[J].现代制造工程, 2015(12):61-64. [6] Chakraborty D, ChoudhuryAR. A semi-analytic approach for direct slicing of free form surfaces for layered manufacturing[J]. Rapid Prototyping Journal, 2008, 13(4):256-264. [7]王春香, 郝志博.快速成型中基于MATLAB软件的STL模型的分层优化[J].机床与液压, 2014, 42(21):113-117. [8]王素,刘恒,朱心雄.模型的分层邻接排序快速切片算法[J].计算机辅助设计与图形学学报, 2011, 23(4):600-605. [9]朱君,郭戈,颜永年.快速成形制造中基于模型连续性的快速分层算法研究[J].中国机械工程, 2000, 11(5):549-554. [10] Hayasi MT, Asiabanpour B.A new adaptive slicing approach for the fully dense freeform fabrication (FDFF) process[J].J Intell Manuf, 2013, 24(4):683-694. [11] S Sikder,A Barari, HA Kishawy. Global adaptive slicing of NURBS based sculptured surface for minimum texture error in rapid prototyping[J]. Rapid Prototyping Journal, 2015, 21(6):649-661. [12]曹丽娜, 田晓霞.三维CAD技术在机械设计中的应用研究[J].装备制造技术, 2014, (6):97-99. [13]张倩.逆向工程在产品创新设计中的实践应用研究[D].太原:太原理工大学,2014.2.2 相交三角形交点计算
2.3 拓扑关系分析
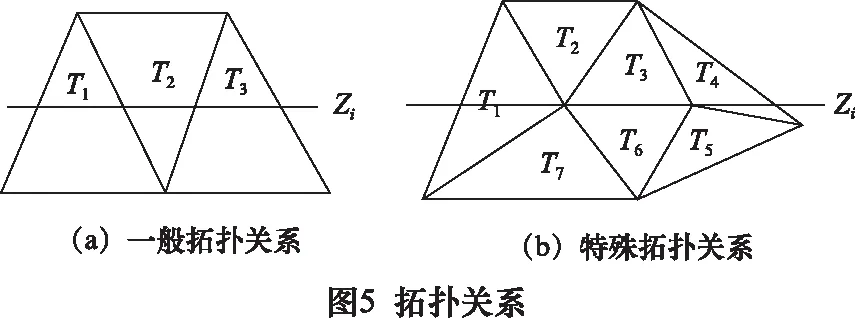
2.4 拓扑关系的重建
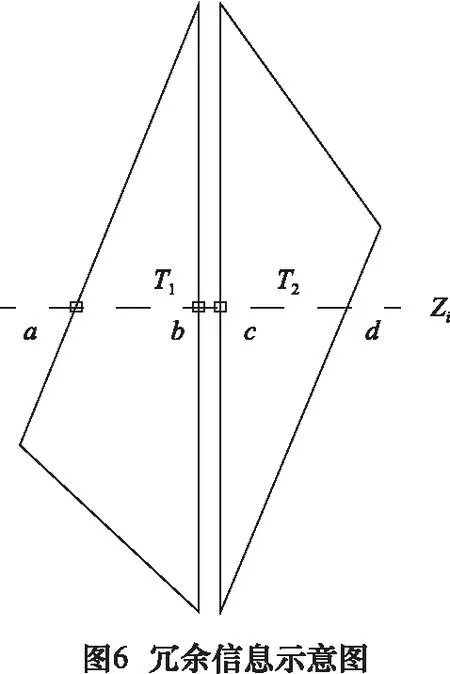
2.5 有序交点的获取与连接
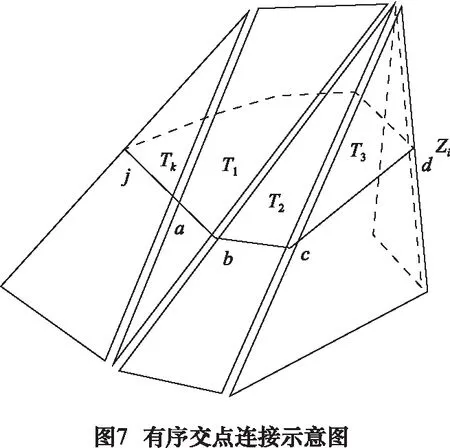
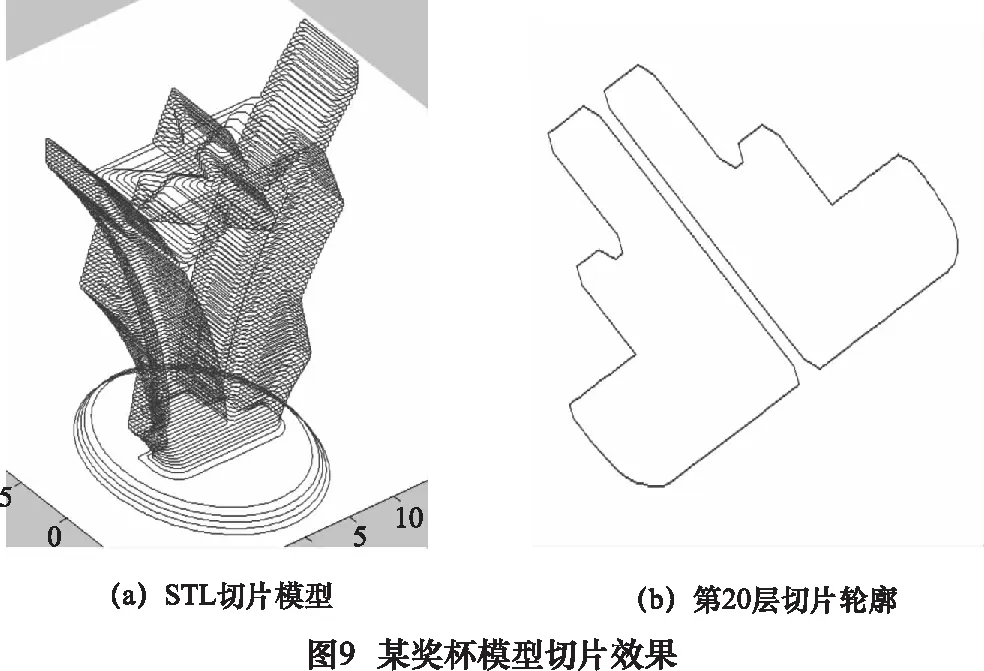
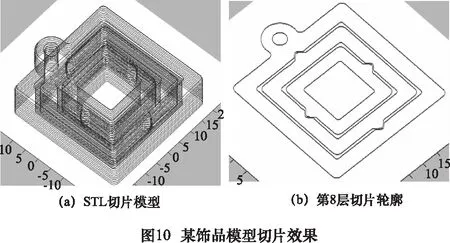
3 实例验证
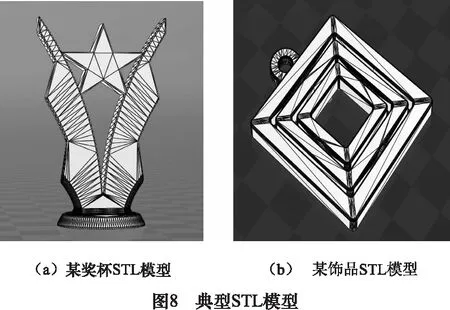
4 结语

