基于最大相关最小冗余联合互信息的多标签特征选择算法

张俐，王枞

（1. 北京邮电大学软件学院，北京 100876；2. 北京邮电大学可信分布式计算与服务教育部重点实验室，北京 100876）

1 引言

近年来，大数据、云计算和人工智能等技术的迅速发展，给人类社会生产和生活带来了前所未有的变化，在这之中就产生了大量的数据[1]。这些数据逐渐呈现出复杂化与高维化的趋势，同时，这些高维数据存在着大量的冗余性和无关性的特征。而这些特征增加了机器学习算法的复杂度和运行时间，同时降低了模型预测的准确性，由此带来了“维数灾难”的问题[2]。特征选择就是通过选取具有代表性的特征子集，用选择好的特征子集代替全集进行学习模型的构建与训练。简单说，特征选择可以通过降低特征维数，提升学习模型的训练速度从而达到比较好的训练效果。它通常的做法是通过挖掘特征与目标对象的相关性以及特征间冗余性的关系寻找最佳的特征子集对象。显然，特征选择算法已经成为大数据、云计算、人工智能背景下企业商务活动和经济决策的重要研究方向，从而引起了国内外众多学者的关注[3～6]。目前，常见的降维方法主要分为2类：特征提取和特征选择。特征提取方法主要是将已经存在的特征集转换为一种新的低维特征空间，新的特征集合是以线性或非线性的方式创建的，它代表的方法有线性判别分析[7]（LDA, linear discriminate analysis）、独立成分分析（ICA, independent component analysis）和主成分分析[8]（PCA,principal component analysis）；而特征选择方法是从原始特征集合中选择出一些最有效的特征以降低数据集维度的过程。目前，特征选择技术大量被应用到数据挖掘、机器学习、图像处理和自然语言处理等方面。特征选择算法主要分为2类：一种是依赖分类器模式（wrapper方法[9]和embedded方法），另一种是不依赖分类器模式（filter方法）。wrapper方法是把各种特征子集当作测试对象，然后通过某个分类器的分类准确率作为该组特征子集性能度量指标，最后根据测试的结果得到最优的特征子集。它的主要问题为：一是计算量非常巨大；二是它采用了穷举的方式去搜索所有可能的特征组合，方法笨拙且不利于推广；三是对某个分类器过分依赖，容易出现“过拟合”现象。embedded方法集成在学习训练过程中，较wrapper方法计算简单而且出现“过拟合”较少，但是寻找适应当前样本的函数模型非常困难。filter方法依据特征与标签的相关性进行特征排序。filter方法主要优点有3个：一是在特征降维方面高效和扩展性强；二是它独立于某个具体的分类器；三是信息论理论广泛应用在filter方法中，使 filter方法拥有比较扎实的理论基础。例如，文献[10～17]提出的互信息、交互信息、条件互信息和联合互信息等。

本文将依赖于信息论的基本理论知识，提出一种新的基于非线性的特征选择方法——JMMC。该算法的目的就是要克服当前 filter方法的某些局限性，例如，对某些特征的高估往往会导致其相关性和冗余性无法识别等问题。同时，本文算法借用前向搜索方法和最大最小的特征选择原则，得到更好的特征子集，它能更高效地处理高维数据集。在UCI中的9个公开数据集中进行实验，结果显示本文所提JMMC方法能够有效地降低数据维度，并且也能够提高不同分类器的分类准确度。

2 相关工作

filter方法[18～24]是当前特征选择的一个研究热点。因此，本节将详细介绍最近几年基于 filter方法的特征选择算法。

互信息法[6,14]主要依赖特征与目标对象的互信息值大小来排列特征的次序。当然在其中可能存在若干个冗余特征。因此，它对于高维特征集合就显得力不从心。

Kwak等[18]提出了统一信息分布下的互信息特征选择（MIFS-U, mutual information feature selection under uniform information distribution）方法去改进MIFS方法，该方法依然采用特征与目标对象去衡量互信息的值，只不过它采用的是基于贪婪性的方法去搜索最有用的特征。

文献[19,20]提出了MIFS方法的改进版本——归一化互信息的特征选择方法（NMIFS），它用标准化的互信息取代了原来的互信息，这种做法的优点可以避免互信息值在多值时取0的可能。

文献[21]提出了联合互信息的特征选择方法（JMI, joint mutual information），他们认为在联合互信息中所选特征子集中特征累加和值最大就是候选特征，那么由这些候选特征构成的特征子集就是最优子集。

Peng等[22]提出了最小冗余最大相关特征搜索（minimal redundancy and maximal relevance）算法以及标准mRMR[23]。它们都使用基于互信息值对特征与类标签集C的相关性以及与所得特征子集S的冗余性进行打分，并将得分最高的特征加入S中。mRMR算法的优点是它将对特征子集的评价转化为对单个特征的评价，同时将当前特征子集中特征间的平均相关性来表示候选特征与当前特征子集之间的冗余性。

文献[15]提出了 FCBF（fast correlation basd filter solution），这是基于系统不确定性原理的特征选择方法。它通过候选特征与类别相关性来进行特征排除，然后采用一个近似马尔可夫毯原理对所得特征子集中冗余特征进行删减。

文献[24]提出了多标签的特征选择算法，它主要通过多标签的方式去寻找重要的特征，从而构成特征子集。

综上所述，目前，绝大多数特征选择算法关注的重点依然是特征与标签之间的相关性和特征之间的冗余性。当然，上面介绍的特征选择方法都有它们各自的局限性。例如，MIFS-U就是当所选特征在增加的时候，特征子集的数目也在增加，同时特征间的冗余性也同样在增加；mRMR和 NMIFS在每次计算中仅涉及2个特征间的冗余性度量，这很容易造成某些特征重要性被过分夸大。

3 最大联合互信息算法分析与研究

3.1 熵、条件熵、互信息和交互信息

定义1 熵[25]是香农在1948年提出的，它主要用来解决信息量化度量的问题。设随机变量Y= {y1,… ,yn}，p(yi)为yi的先验概率，那么H(Y)的熵就可以表示为

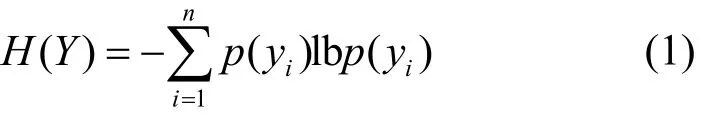
从式(1)可知，Y不确定性越大，H(Y)也就越大，那么所需要的信息量也就越大。

定义2 设随机变量X= {x1,… ,xn}，p(xi)为xi的先验概率，Y={y1,… ,ym}，p(yj)为yj的先验概率，那么随机变量X和随机变量Y的联合可以熵表示为

定义3 设随机变量X= {x1,… ,xn}，p(xi)为xi的先验概率，Y={y1,… ,ym}，p(yj)为yj的先验概率，那么随机变量Y下随机变量X的条件熵可以表示为

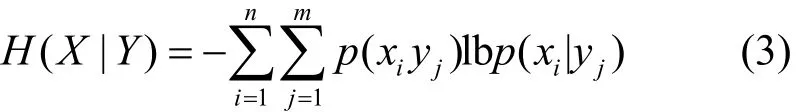
定义 4 条件熵与联合熵之间的关系如式(4)所示。

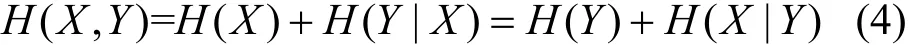
定义 5 互信息[6]是信息论里的一种信息度量工具，它表示一个随机变量X中包含的关于另一个随机变量Y的信息量。设变量X和变量Y，联合概率密度函数是p(xy)，它们边缘概率密度函数分别是p(x)、p(y)，那么它们的互信息I(X;Y)可以表示为

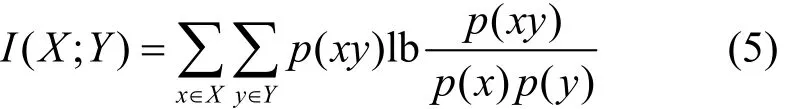
同理，根据式(1)～式(5)，互信息与熵、条件熵和联合熵之间的关系可以表示为

定义6 条件互信息。设有3个随机变量分别是X、Y、C，它们的联合概率密度函数分别是p(XYC)、p(X|C)和p(Y|C)以及条件概率密度函数p(XY|C)，假设随机变量C是已知的，那么随机变量X和随机变量Y关于随机变量C的条件互信息I(X;Y|C)可以表示为

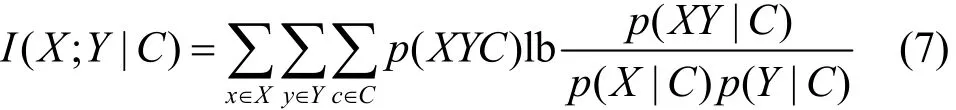
依据互信息和熵的定义，联合互信息可以表示为

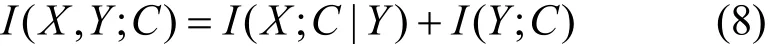
定义7 交互信息[26]是指在任何特征子集中不存在，但是它却被所有特征所共享的信息。通常，交互信息I(X;Y;C)与联合互信息、互信息之间的关系可以表示为

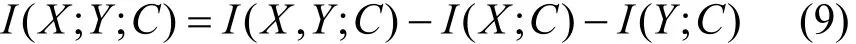
通常来说，交互信息值可以是正、负或 0。当随机变量X、Y组合在一起共同提交的信息不包含它们各自提交的信息时，交互信息表示为正，而最大交互信息是指随机变量X、Y组合在一起所获得的最大信息值；当随机变量X、Y各自提交信息包括某些相同的一些信息时，交互信息表示为负；当随机引入某个随机变量时，并不影响随机变量X（或Y）和C之间的关系时，交互信息表示为0。

3.2 特征的相关性、冗余性和交互信息

特征相关性的分析是描述特征重要性的关键方法之一。在信息论中，特征的相关性根据其特点可以分为相关、冗余、无关和交互。John等[27]将特征分为3类：强相关、弱相关和无关特征。而在一个最优特征集合中通常应该包括所有的强相关特征和一部分弱相关特征，不包括无关特征等。由于弱相关特征的组成相当复杂，如何从这些特征中进一步筛选出冗余特征，对特征选择算法性能提升至关重要。文献[18～24]提出了许多特征选择算法中都存在着选择了一些冗余和不相关的特征。

因此，下面将结合信息论中互信息、条件互信息和交换信息的概念，给出判断特征相关性的标准。

定义8 假设数据样本集D= (T,F,C)，n表示样本的数量，样本空间维数为m，T= {t1,… ,tn}表示样 本 集 合 ，C= {c1,… ,ck}表 示 标 签 集 合 ，F= {f1,… ,fm}表示特征集合。fi∈F,fj∈F，其中fi≠fj。S⊂F表示S是F的子集，S′=F−S表示S′是F的子集。

定义 9 特征相关性。在S已知的情况下，当fi∉S、fj∉S时，如果存在I(fi,C;S) ＞I(fj,C;S)，就表示fi与目标标签C的相关性大于fj与目标标签C的相关性。那么，可以进一步推导出，如果fi与fj存在依赖关系，并且fi∉S，S=fj∪S，就可以说明特征fi与目标标签C的相关性会因为fj的加入而提高，即I(fi,C;S) ＞I(fi,C)。

定义10 特征冗余性。在S已知的情况下，如果fi与fj存在依赖关系，fj是冗余特征，并且fi∉S，S=fj∪S，那么就可以说明特征fi与目标标签C的相关性会因为fj的加入而减少，即I(fi,C;S)＜I(fi,C)。同时，也可以进一步表示为I(F;C)≤I(S;C) +I(S′;C)。

定义11 特征无关性。在S已知的情况下，如果fi与fj之间是无关的，即表示fi与fj相互独立，那么就可以说明特征fi与目标标签C的相关性不会因为fj的加入而提高，即I(fi,C;S) =I(fi,C)。

定义12 特征间交互信息。设fi∈S′，fj∈S，根据式(9)，如果I(F;C)≥I(S;C) +I(S′;C)，就表示在F集合中的任何一个特征的缺失都会导致降低对目标标签C的预测能力。同时，交互信息值还可以进一步表示为当不同的特征fj加入S时，特征fi与目标标签S的相关性的值就可以表示为I(fi,C;fj)，那么加入的特征的最小值就可以表示为

3.3 算法推导

从3.2节可以知道，特征之间、特征与目标标签C之间的相关性完全可以通过I(S′,C;S)与I(S′;C)、I(S′;S)之间的大小差值进行确定。因此，I(S′,C;S)与I(S′;C)、I(S′;S)之间的关系决定了该特征是否是相关特征、冗余特征和无关特征。

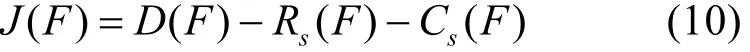
根据文献[3]和文献[11]，给出特征评价准则为其中，D(F)表示特征F与标签C的相关性；Rs(F)表示特征F与所选择集合S中的特征之间的冗余性；Cs(F)表示特征F与所选择集合S中的特征之间的交互信息。

再根据式(8)～式(10)以及文献[21]就可以推导出最终所要的结果

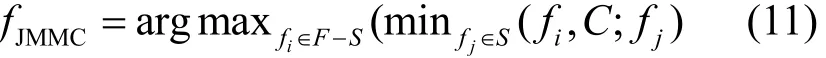
将式(11)右边计算式展开，设fi、fj为特征，C为标签，fi∈F−S，fj∈S，ijf≠f，根据交互信息规则[24]又有

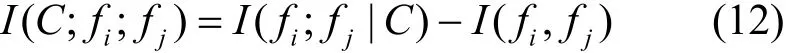
结合式(4)～式(12)，有

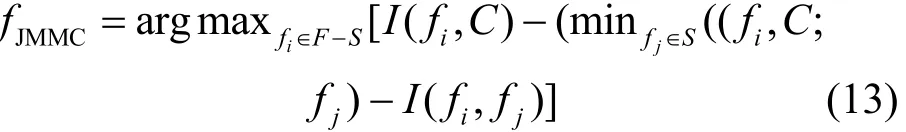
在实际中，I(fi;fj|C)求解非常困难，因此本文结合文献[11,28～30]给出一种近似求解方法。

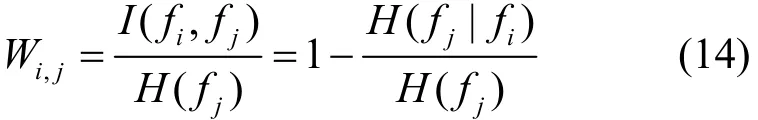
令当C给定时，Wi,j会因为C的存在而不发生任何变化。因此，可以得出

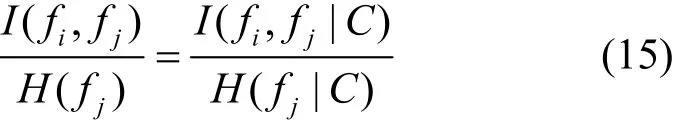
最后综合式(13)～式(15)可以得出

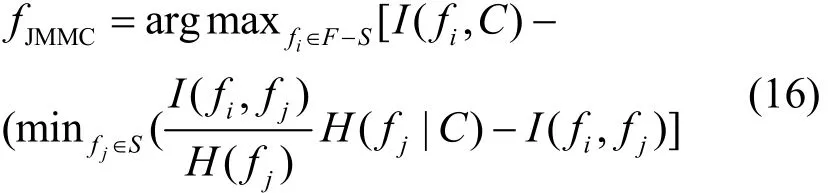
3.4 算法描述

通过上面的分析可以知道，在进行特征选择时，除了要充分考虑特征相关性、冗余性外，还要考虑特征间与标签之间的交互信息，而在第 2节所分析的特征排序算法中，有些算法只是考虑了特征与标签之间的相关性；有些算法在考虑特征与标签之间的相关性以及特征与特征之间的冗余性的同时，却往往忽略了特征之间还有交互信息的存在[31～36]。因此，本文提出了最大联合互信息算法（JMMC），充分考虑了特征与标签之间的相关性，更进一步考虑了某些重要特征对标签乃至整个数据集产生的影响，并且也兼顾考虑了特征与特征之间交互信息，同时也借用了最大相关最小冗余的思想。下面，给出JMMC特征选择算法伪代码实现，具体如算法1所示。

算法1 JMMC特征选择

输入 原始数据集D；原始特征集F；类标签集合C

输出 期望所选的特征排序集S

1) 初始化

2)S←φ;

3) 计算最大互信息

4) for each ∀fi∈Fdo

5) 计算每一个特征的互信息I(fi;C)，并存入relevant_mi_set集合中

6)fmax=max_sort(relevant_mi_set)

7)F←Ffmax;S←fmax

8) 使用贪婪搜索方法寻找下一个特征

9) repeat untilF集合不为空：

10) 选择下一个特征方法：

11) 根据式(16)进行计算

12)F←Ffmax

13)S←S∪fmax

14) 当F集合为空时，跳出循环

15) 输出所要的排序集合S

步骤1)～步骤2)，初始化最优特征集S；步骤3)～步骤7)，选择和标签类别相关性最大的特征变量，存入S集合中；步骤8)～步骤14)，使用前向贪婪性搜索方法并结合式(16)，得到与标签最大相关且与其他特征两两之间最小冗余的特征fmax并加入S中，循环结束的标志是F特征集合为空。步骤15)，算法就得到了最优集S。

4 实验研究

本节将对JMMC算法进行有效性验证，主要从以下 2个方面证明其有效性：1) 看 JMMC算法是否具有特征降维效果，并能同时提高模型的准确度；2) 与其他特征选择方法相比较，JMMC算法是否能有更好的降维效果。本文实验的研究框架具体如图1所示。

4.1 特征选择方法

JMMC算法在设计之初，就充分考虑了特征与标签的相关性以及特征之间的冗余性和交互信息，目的是有效地识别在特征集合中是否有冗余特征和无关特征的存在。为了解决上面实验考虑的问题，本文选择4类具有代表性的特征选择方法作为 JMMC算法的比较对象，它们分别是FullSet、IG、ReliefF和 FCBF。

1) FullSet方法就是原始特征集合，选择它的目的就是要研究JMMC算法做的特征选择是否真的有效，即是否具有特征降维效果，并同时提高模型的准确度。

2) IG全称为信息增益（information gain）[6,14]，是一种经典的特征排序算法，它主要研究候选特征与标签的相关性，也就是说候选特征与分类标签越相关，它们之间的信息增益越大，该特征越重要。最后，根据特征与标签的相关性大小顺序，进行特征排序并输出。因此，IG特征算法是特征选择领域中检验所提算法有效性时最常见的基准算法之一。

3) ReliefF算法[11]是一种经典的基于特征距离的排序算法。它从样本中的类内距离和类间距离来衡量特征之间的差异。一般认为好的特征应该属于同一类并且是该样本的最近的邻居，而属于不同标签的样本应该在该特征上取值尽可能不同。在本文中，ReliefF算法中近邻数和设置为 5。

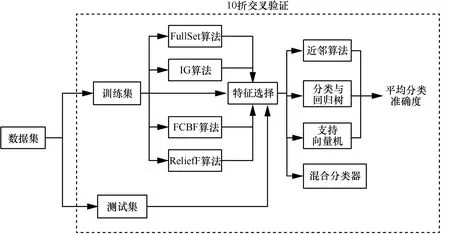
图1 研究框架

4) FCBF算法在第2节已有介绍，在此不再赘述。

4.2 分类模型

本文的实验环境是lenovo-ThinkPad笔记本，处理器是 Intel(R)-Core(TM) i7-4500UCPU@1.80 GHz,2.4 GHz，内存是8 GB，Windows 7 64位操作系统，pycharm和 Anaconda2-(64-bit)开发环境，python的运行环境版本是2.7.12。同时，本文采用几种频率高的分类器模型，具体如下所示。

1) 近邻（KNN,k-nearest neighbor）算法，指当一个样本在特征空间中有k个最相邻的样本，而这些样本中的大多数属于某一个类别，那么该样本也属于这个类别。KNN近邻分类器是最为经典的分类器算法。KNN的近邻数设置为3。

2) 分类与回归树（C4.5, classification and regression tree）算法通过entropy或基尼系数来选择特征进行分叉。最终将具有p维特征的n个样本分到c个类别中去。在本文中，C4.5采用基尼系数进行特征分叉。

3) 支持向量机（SVM, support vector machine），指通过升维把低维样本向高维空间做映射，使原本在低维样本空间中非线性可分的问题转化为在特征空间中线性可分的问题。SVM分类器的参数都使用sklearn包的默认参数设置。

4) 混合分类器，就是将3KNN、C4.5和SVM进行混合来看它们整体的分类结果，在这里，3KNN、C4.5和SVM中的权重均取。

4.3 实验数据集

本文选择的实验数据全部来自国际通用的UCI机器学习的数据集，它们分别是 heart、dermatology、movement_libra、wdbc、arrhythmia、musk、mfeat-kar、mushroom、kr-vs-kp这 9个数据集，详细内容如表1所示。样本数据分类数为2～15个，样本数为270～8 124个，样本的特征数为14～279维。为了保证数据更有说服性，整个实验过程采用 10折交叉验证[37]对实验数据集进行测试和评价，最后，通过对10次实验求均值得到最后的实验结果。

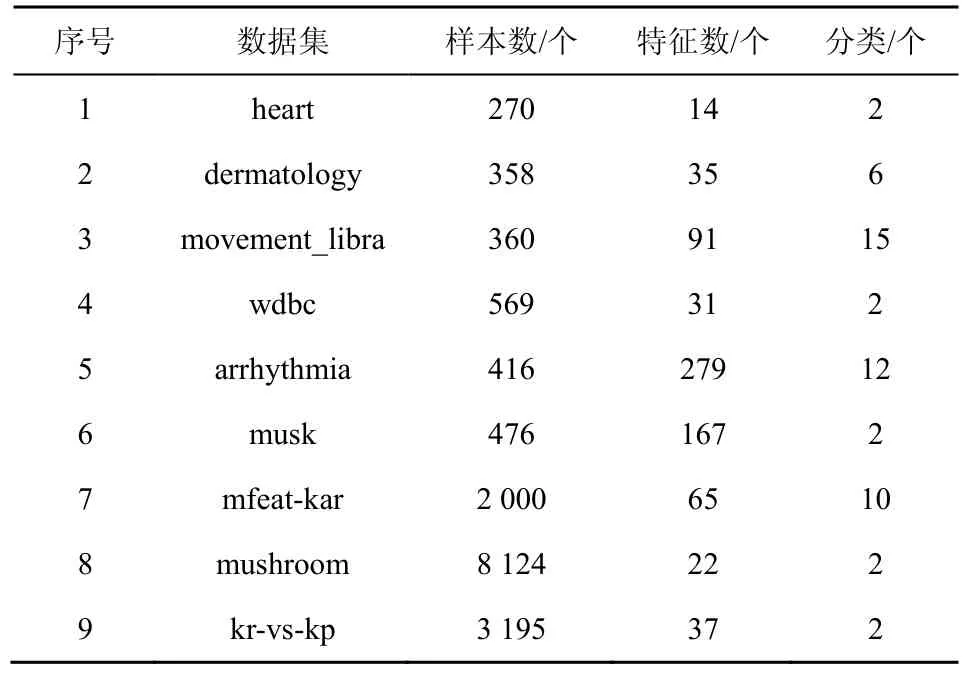
表1 实验中的UCI数据集

4.4 实验结果分析

本文均采用Accuracy预测特征算法的优劣。同时，为了进一步说明不同算法在不同分类器和数据集的优劣，本文使用 Win/Draw/Loss来统计并分析算法两两之间的差异。Win表示算法A好于B，Draw表示算法A等于B，Loss表示算法A差于B。

4.5 小样本低维数据集的分析

在小样本数据集合中，平均样本数为390个，平均特征数为 42.75。表 2～表 4给出了所选择 4种数据集上不同分类器（3KNN、C4.5和SVM）采用 10折交叉验证法所获得的平均分类准确率和特征数。表5给出了所选择4种数据集上混合分类器（由3KNN、C4.5和SVM组成）采用10折交叉验证法所获得的平均分类准确率和特征数。图2～图5给出了这4种数据集合的显示混合分类器效果，其中，横坐标表示依次递増的所选特征子集数目，纵坐标表示平均分类率准确率。根据表 2～表 5以及图 2～图 5所示的实验结果，JMMC算法使用3KNN分类器在heart数据集、dermatology数据集、movement_libra数据集和wdbc数据集上比FullSet要高出4.074%、0.833%、0.666%和1.391%；并且，JMMC算法使用C4.5分类器在 heart数据集、dermatology数据集、movement_libra数据集和 wdbc数据集上比FullSet要高出1.852%、0.833%、0.666%和1.391%；JMMC算法使用 SVM 分类器在 heart数据集、dermatology数据集、movement_libra数据集和wdbc数据集上比FullSet要高出1.481%、0.294%、

0.889%和 5.596%；JMMC算法使用混合分类器在heart数据集、dermatology数据集、movement_libra数据集和wdbc数据集上比FullSet要高出10.745%、1.23%、0.889%和6.625%。通过对以上4种数据集在不同分类器以及它们的混合分类器来看，JMMC算法均起到了降低数据冗余度、提高分类准确度的效果，同时，从表2～表5可以看出，由于分类器从弱变强，分类的效果也会变好，并且所需要的平均特征数也会相应减少。现在，再来对比JMMC算法和其他特征排序算法，从表2～表5可以看出，JMMC算法在绝大多数情况下均优于其他所选择的特征排序算法，具体描述可以从表6看出。

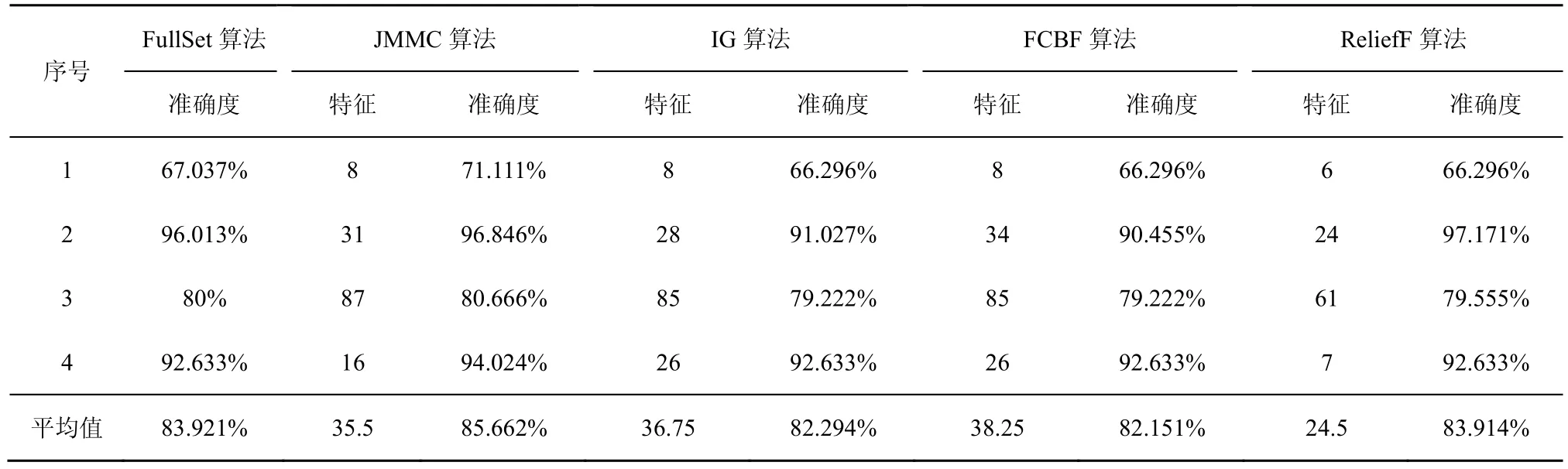
表2 基于3KNN分类器的所选特征集平均准确率

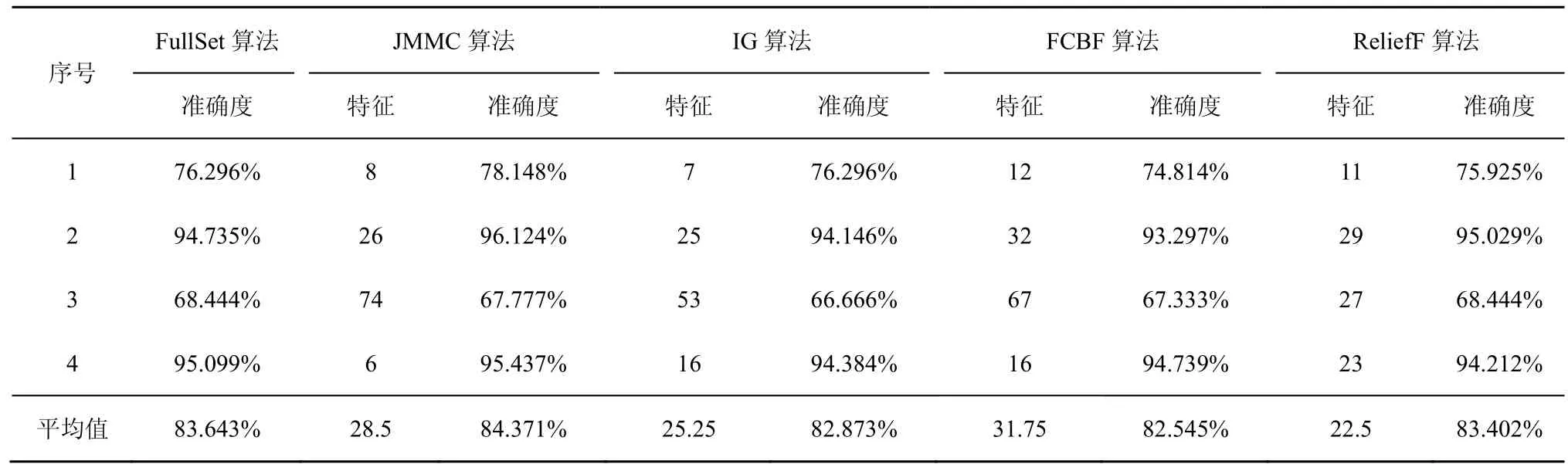
表3 基于C4.5分类器的所选特征集平均准确率

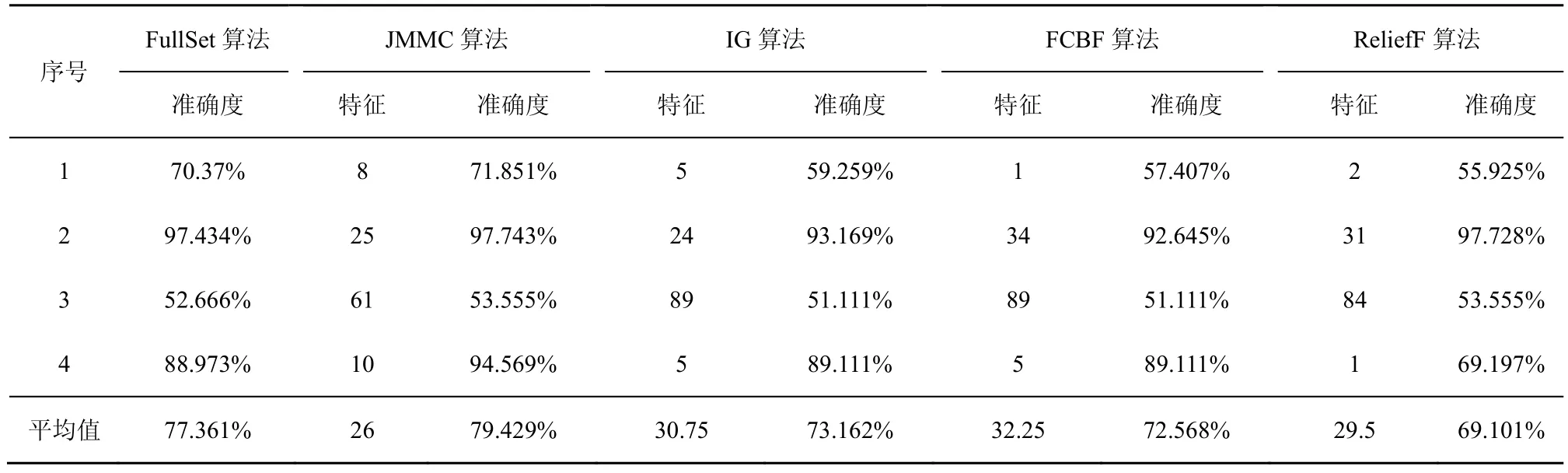
表4 基于SVM分类器的所选特征集平均准确率

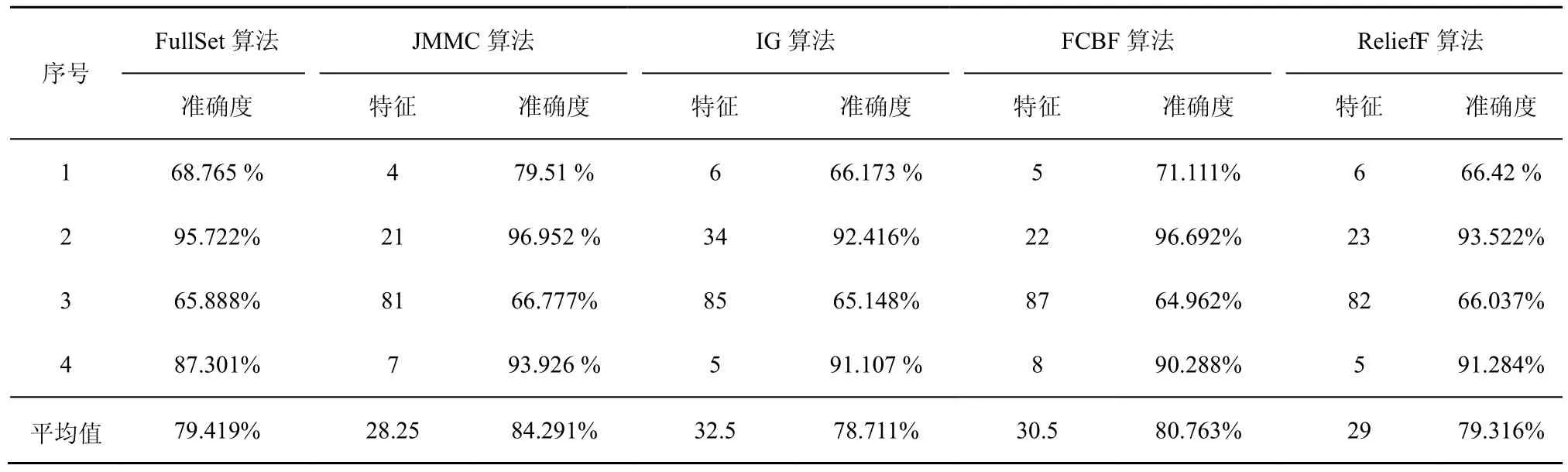
表5 基于混合分类器和不同算法的平均准确率

综上可得，在小样本集中，JMMC算法在特征的选择上由于更多地考虑了特征间冗余性与交互信息，所以说分类的准确率更好一些。

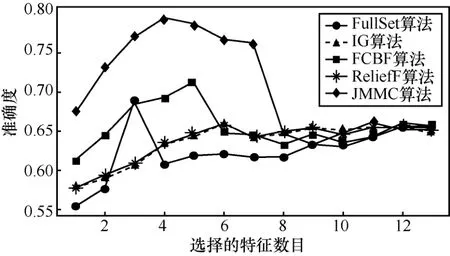
图2 heart数据集不同算法的平均正确率

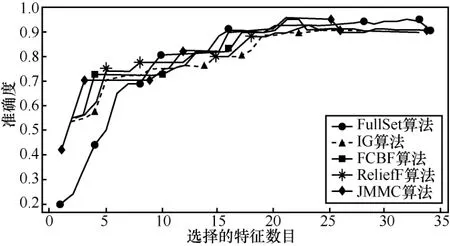
图3 dermatology数据集不同算法的平均正确率

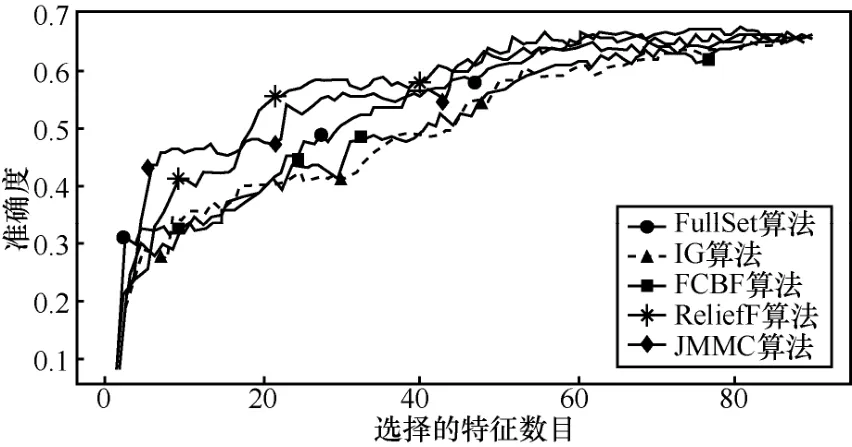
图4 movement_libra数据集不同算法的平均正确率

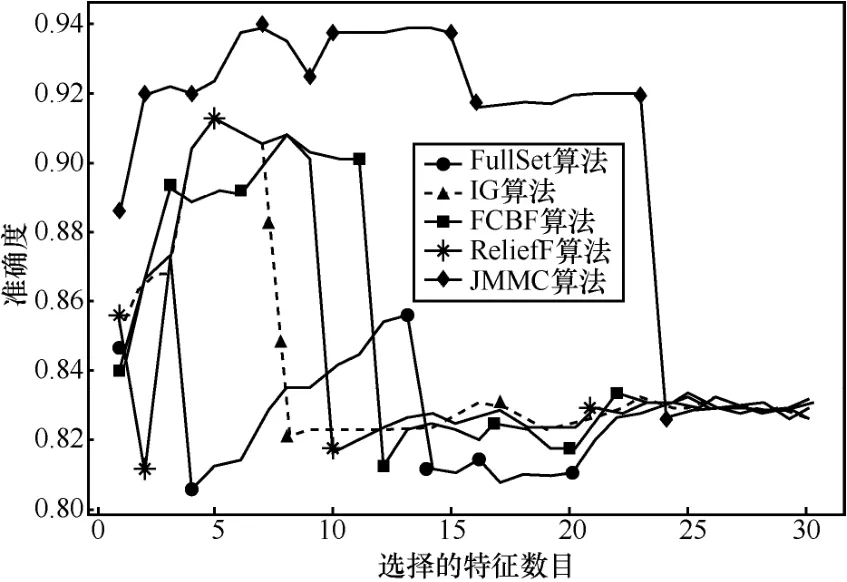
图5 wdbc数据集不同算法的平均正确率

4.6 大样本高维数据集的分析

在大样本数据集合中，平均样本数是2 843个，平均特征数为114。表7～表9给出了所选择5种数据集上不同分类器（3KNN、C4.5和SVM）采用 10折交叉验证法所获得的平均分类准确率和特征数。表10给出了所选择5种数据集上混合分类器（由3KNN、C4.5和SVM组成）采用10折交叉验证法所获得的平均分类准确率和特征数。图6～图10给出了这5种数据集合的显示混合分类器效果，其中横坐标表示依次递増的所选特征子集数目，纵坐标表示平均分类率准确率。根据表7～表10以及图6～图10所示的实验结果，JMMC算法使用 3KNN分类器在 arrhythmia数据集、musk数据集、mfeat-kar数据集、mushroom数据集和kr-vs-kp数据集上比FullSet要高出0.933%、1.549%、0、0和 3.538%；并且，JMMC算法使用C4.5分类器在arrhythmia数据集、musk数据集、mushroom数据集和kr-vs-kp数据集上比FullSet要高出5.456%、0.195%、0和0；JMMC算法使用SVM分类器在arrhythmia数据集、musk数据集、mfeat-kar数据集、mushroom数据集和 kr-vs-kp数据集上比FullSet要高出2.066%、2.789%、0、1.476%和 0；JMMC算法使用混合分类器在arrhythmia数据集、musk数据集、mfeat-kar数据集、mushroom数据集和 kr-vs-kp数据集上比FullSet要高出1.082%、0.286%、0.133%、0.607%和 1.18%。从以上的数据分析可以看出，JMMC算法只是在使用C4.5分类器时在mfeat-kar数据集上略低于FullSet，其他均优于或等同于FullSet。同时，通过对以上5种数据集在不同分类器以及它们的混合分类器来看，JMMC算法起到了降低数据冗余度、提高分类准确度的效果，同时，从表 8～表 10可以看出，由于分类器从弱变强，分类的效果也会变好，并且，所需要的平均特征数也会相应减少，其中在基于 SVM 的分类器表现得尤为明显，特征数平均只需要32.4个。现在，再来对比JMMC算法和其他特征排序算法，从表7～表9可以看出，JMMC算法大部分均优于其他所选择的特征排序算法，可能由于分类器的原因造成在个别数据集上和不同分类器上存在JMMC算法略低于其他特征排序算法，这些具体情况都可以从表11看出。现在，可以得出在大样本集中，JMMC算法在特征的选择上由于充分地考虑了特征间冗余性与交互信息，分类准确率相比其他算法要更好一些。

表6 JMMC算法与其他基于特征排序算法的Win/Draw/Loss分析

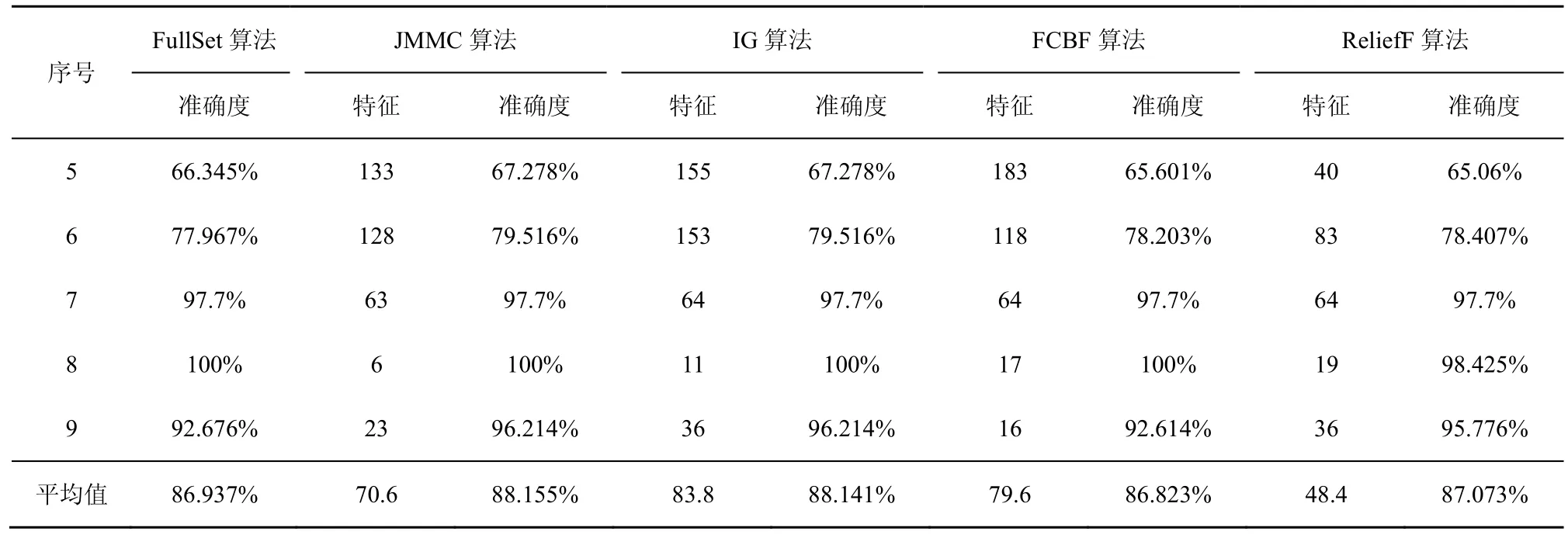
表7 基于3KNN分类器的所选特征集平均准确率

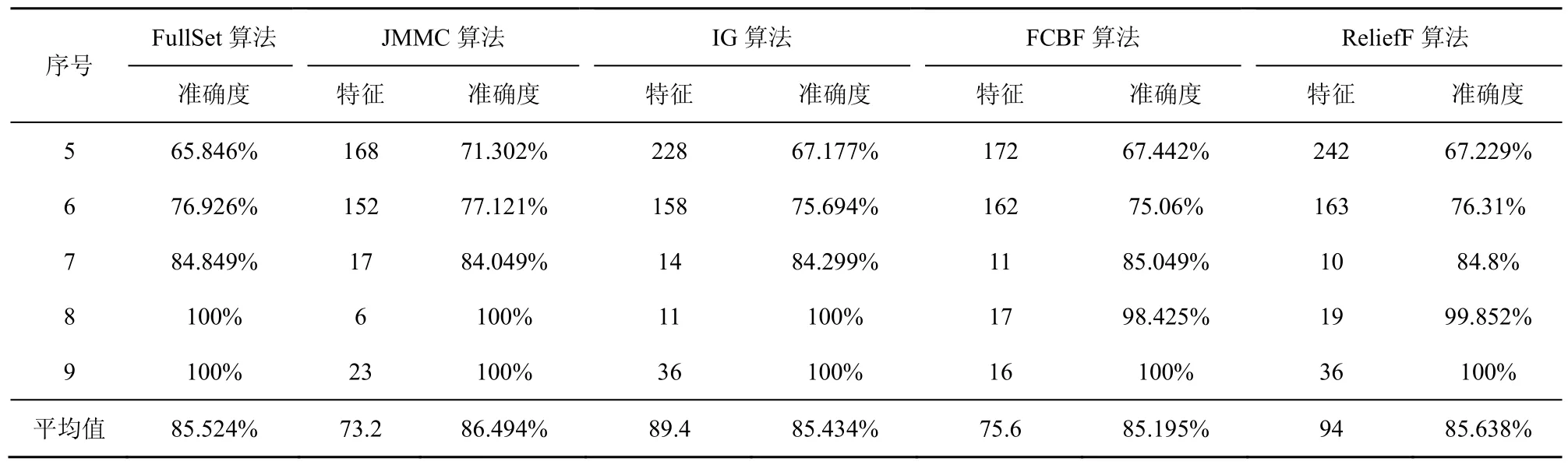
表8 基于C4.5分类器的所选特征集平均准确率

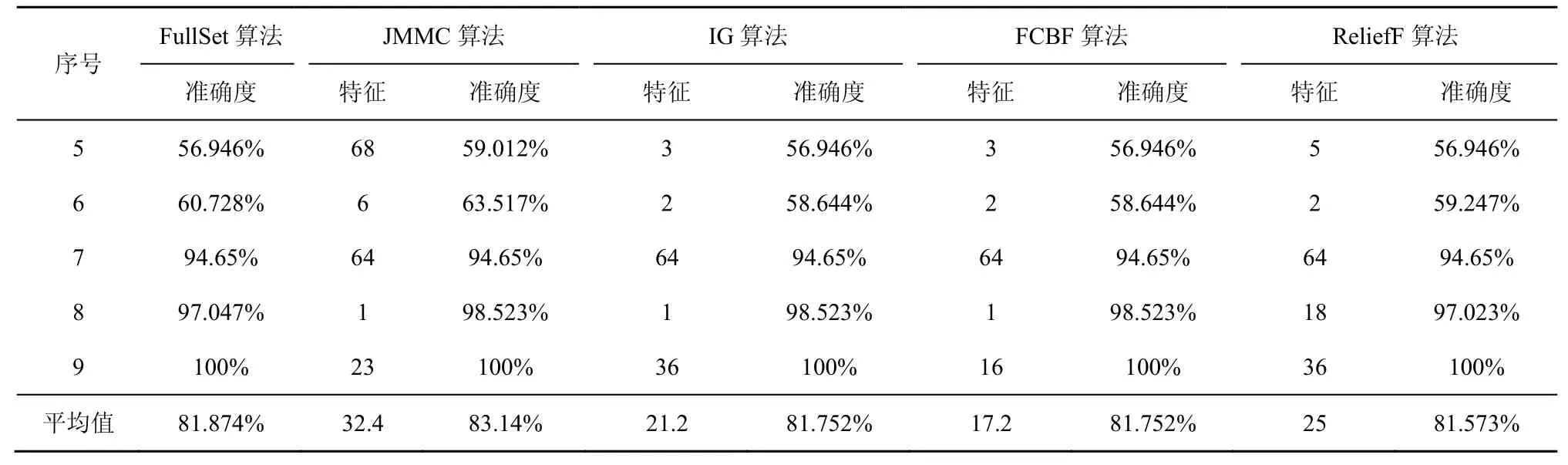
表9 基于SVM分类器的所选特征集平均准确率

表10 基于不同分类器和不同算法的平均准确率

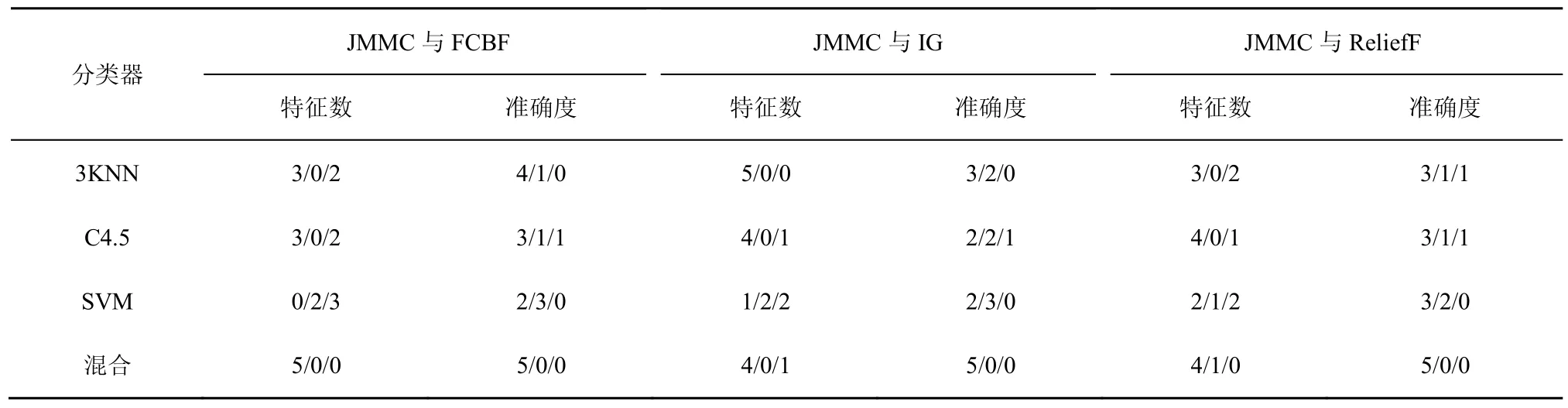
表11 JMMC算法与其他基于特征排序算法的Win/Draw/Loss分析

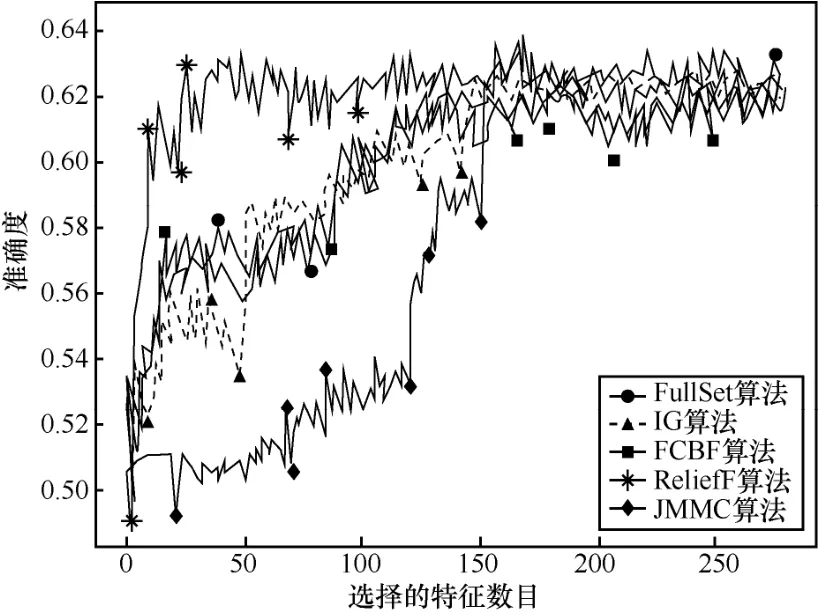
图6 arrhythmia数据集不同算法的正确率

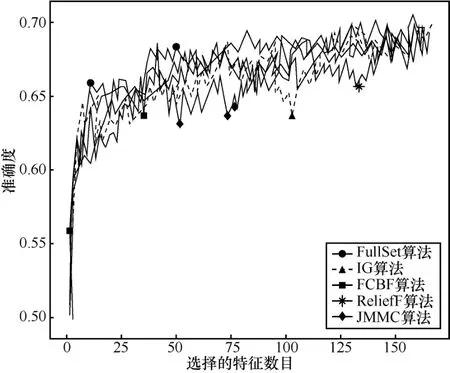
图7 musk数据集不同算法的平均正确率

图8 mfeat-kar数据集不同算法的平均正确率

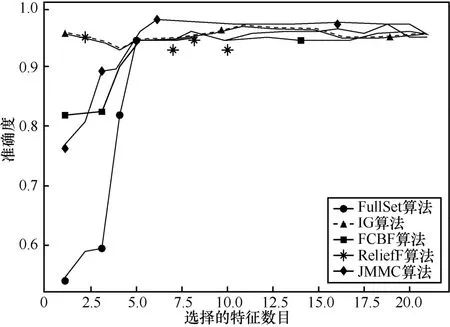
图9 mushroom数据集不同算法的平均正确率

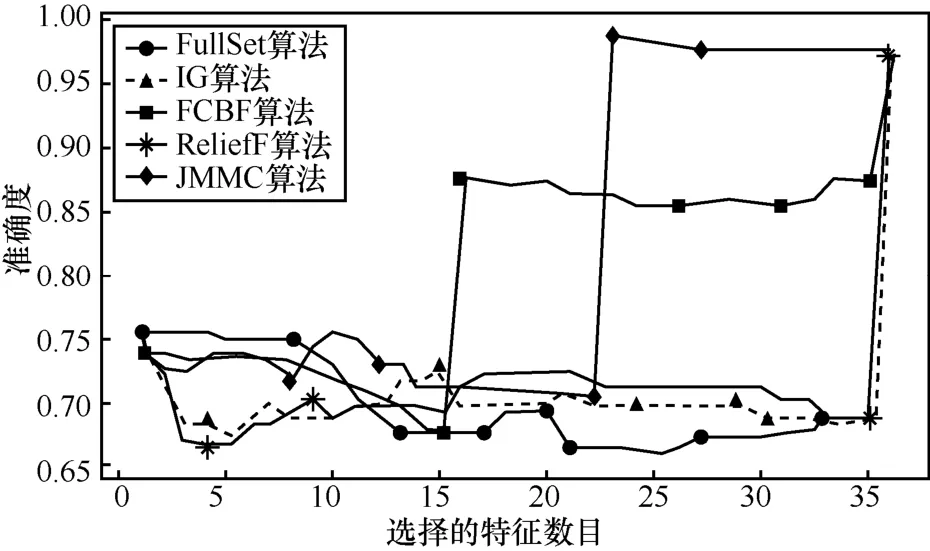
图10 kr-vs-kp数据集不同算法的平均正确率

5 结束语

特征选择算法主要是尽可能寻找较小的特征子集，从而获得较高分类预测准确率。本文通过引入条件互信息和交互信息，并依赖最大最小原则建立新的特征排序算法（JMMC算法）。它不仅考虑特征的相关性、冗余性和无关性，也充分考虑了特征间与目标标签之间的交互信息。首先，依据信息论理论，重新定义了相关性、冗余性、无关性和交互信息。其次，给出了 JMMC算法的推导和实现过程。在UCI公开的9个样本集和4种不同的分类器（3KNN、C4.5、SVM和混合分类器）中，JMMC算法在绝大多数情况下，平均分类准确率均优于其他特征排序算法。

综上可知，JMMC算法不仅能有效识别出相关特征、冗余特征和无关特征，而且也能识别出特征间产生交互信息的那些特征。因此，JMMC算法可以有效地提高分类的准确度，并且降低特征的维数。下一步的工作将是对交互信息、条件互信息等理论进行更进一步的研究，以便能提出更加有效的特征排序算法来优化选择出的特征子集并进一步提高它们分类的准确率。

[1] GEORGE G, HAAS M R, PENTLAND A. Big data and management[J]. Academy of Management Journal,2014,57(2)∶321-326.

[2] XIE J Y, XIE W X. Several selection algorithms based on the discernibility of a feature subset and support vector machines[J].Chinese Journal of Computers, 2014,37(8)∶1704-1718.

[3] BROWN G, POCOCK A, ZHAO M J, et al. Conditional likelihood maximisation-a unifying framework for information theoretic feature selection[J].Journal of Machine Learning Research, 2012,13∶27-66.

[4] CHENG H G, QIN Z, FENG C, et al. Conditional mutual information based feature selection analysing for synergy and redundancy[J].Electronics and Telecommunications Research Institute, 2011(33)∶210-218.

[5] CHANDRASHEKAR G, SAHIN F .A survey on feature selection methods[J].Computers and Electrical Engineering, 2014(40)∶16-28.

[6] ZHANG Z H, LI S N, LI Z G, et al. Multi-label feature selection algorithm based on information entropy[J].Journal of Computer Research and Development, 2013,50(6)∶1177-1184.

[7] YU H, YANG J.A direct LDA algorithm for high-dimensional data with application to face recognition[J].Pattern Recognition, 2001(34)∶2067-2070.

[8] BAJWA I S, NAWEED M S, ASIF M N, et al. Feature based image classification by using principal component analysis[J].ICGST International Journal on Graphics Vision and Image Processing, 2009(9)∶ 11-17.

[9] MALDONADO S, WEBER R. A wrapper method for feature selection using support vector machine[J].Information Science, 2009, 179(13)∶2208-2217.

[10] PENG C. DistributedK-Means clustering algorithm based on Fisher discriminant ratio[J].Journal of Jiangsu University, 2014, 35(4)∶422-427.

[11] ZHANG Y S, YANG A, XIONG C, et al. Feature selection using data envelopment analysis[J].Knowledge-Based Systems,2014(64)∶70-80.

[12] YU L, LIU H. Feature selection for high-dimensional data∶ a fast correlation-based filter solution[C]//The 20th International Conferences on machine learning. 2003∶ 856-863.

[13] HUANG D, CHOW T W S. Effective feature selection scheme using mutual information[J]. Neurocomputing,2005 (63)∶325-343.

[14] LIU H W, SUN J G, LIU L, et al. Feature selection with dynamic mutual information[J]. IEEE Transactions on Neural Networks, 2009,20(2)∶ 189-201.

[15] DUAN H X, ZHANG Q Y, ZHANG M.FCBF algorithm based on normalized mutual information for feature selection[J].Journal Huazhong University of Science & Technology(Natural Science Edition), 2017,45(1)∶52-56.

[16] SUN G L, SONG Z C, LIU J L, et al. Feature selection method based on maximum information coefficient and approximate markov blanket[J]. Acta Automatica Sinica, 2017,43(5)∶795-805.

[17] VERGARA J R, ESTEVEZ P.A review of feature selection methods based on mutual information[J].Neural Computing and Applications,2014,24(1)∶175-186.

[18] KWAK N, CHOI C H. Input feature selection for classification problems[J]. IEEE Transactions on Neural Networks, 2002(13)∶143-159.

[19] ESTÉVEZ P A, TESMER M, PEREZ C A, et al. Normalized mutual information feature selection[J].IEEE Transaction on Neural Networks,2009(20)∶189-201.

[20] HOQUE N, BHATTACHARYYA D K, KALITA J K.MIFS-ND∶a mutual information-based feature selection method[J]. Expert Systems with Applications,2014,41(14)∶6371-6385.

[21] HOWARD H Y, JOHN M. Feature selection based on joint mutual information[C]//Advances in Intelligent Data Analysis (AIDA), Computational Intelligence Methods and Applications (CIMA), International Computer Science Conventions Rochester New York. 1999∶ 1-8.

[22] PENG H, LONG F, DING C, Feature selection based on mutual in-formation∶ criteria of max-dependency, max-relevance, and min- redundancy[C]//IEEE Transaction on Pattern Analysis & Machine Intelligence. 2005, 27 (8)∶ 1226-1238

[23] VINH L T, THANG N D, LEE Y K. An improved maximum relevance and minimum redundancy feature selection algorithm based on normalized mutual information[C]//Tenth International Symposium on Applications and the Internet. 2010∶ 395-398.

[24] LEE J, KIM D W. Mutual information-based multi-label feature selection using interaction information[J].Expert Systems with Applications,2015(42)∶ 2013-2025.

[25] COVER T, THOMAS J.Elements of theory[M]. New York∶ John Wiley & Sons, 2002.

[26] JAKULIN A. Attribute interactions in machine learning (Master thesis)[M]//Lecture Notes in Computer Science. 2003.

[27] JOHN G H, KOHAVI R, PFLEGER K. Irrelevant features and the subset selection problem[C]//The Eleventh International Conference on Machine Learning, 1994∶ 121-129.

[28] BENNASAR M, HICKS Y, SETCHI R. Feature selection using Joint mutual information maximisation[J]. Expert System Application,2015(42)∶ 8520-8532.

[29] ZHANG Y S, ZHANG Z G. Feature subset selection with cumulate conditional mutual information minimization[J]. Expert Systems with Applications, 2012,39(5)∶6078-6088.

[30] YU L, LIU H. Efficient feature selection via analysis of relevance and redundancy[J]. Journal of Machine Learning Research, 2004, 5(12)∶1205-1224.

[31] TAPIA E, BULACIO P, ANGELONE L F. Sparse and stable gene selection with consensus SVM-RFE[J]. Pattern Recognition Letters,2012,33(2)∶164-172.

[32] UNLER A, MURAT A, CHINNAM R B. mr2PSO∶ a maximum relevance minimum redundancy feature selection method based on swarm intelligence for support vector machine classification[J]. Information Sciences, 2011(20)∶ 4625-4641.

[33] CHE J X, YANG Y L LI L, et al. Maximum relevance minimum common redundancy feature selection for nonlinear data[J]. Information Sciences, 2017(5)∶68-89.

[34] CHAKRABORTY R, PAL N R. Feature selection using a neural framework with controlled redundancy[J].IEEE Transactions on Neural Networks and Learning Systems, 2015,26 (1) ∶35-50.

[35] AKADI A E, OUARDIGHI A, ABOURAJDINE D.A powerful feature selection approach based on mutual information[J]. International Journal of Computer Science and Network Security, 2008(8)∶116-211.

[36] FLEURET F. Fast binary feature selection with conditional mutual information[J]. Journal of Machine Learning Research, 2004(5)∶1531-1555.

[37] NIU X T. Support vector extracted algorithm based on KNN and 10 fold cross-validation method[J].Journal of Huazhong Normal University, 2014,48(3)∶335-338.