快速移不变稀疏分类算法在线识别汽油机故障

张晓焱，刘 永

ZHANG Xiaoyan1，2,LIU Yong1

1.南京理工大学 计算机科学与工程学院，南京 210094

2.南京交通职业技术学院，南京 211188

1.School of Computer Science and Engineering,Nanjing University of Science and Technology,Nanjing 210094,China

2.Nanjing Vocational Institute of Transport Technology,Nanjing 211188,China

故障诊断技术对汽油发动机的动力性、经济性、排放、工作寿命以及行车安全都有着非常重要的意义。虽然OBD（车载自诊断系统）能够对电控系统器件的异常进行检测和诊断，但是对于一些微小的机械故障却难以给出及时准确的诊断结果。鉴于汽油发动机复杂的非线性时变特性，难以通过建立精确模型的方式来识别故障。目前，直接通过对发动机电控系统产生的工况数据流进行分析的方法得到了越来越广泛的应用[1-2]。常见方法有基于时域趋势和频谱分析的信号处理法，基于支持向量机、神经网络、聚类和隐马尔科夫的模式识别法等。近年来，稀疏编码技术的逐渐兴起为数据分析提供了新的渠道。Wright等基于稀疏理论提出了稀疏分类算法（Sparse Representations Classification，SRC），并在故障识别领域取得了很好的效果[3-7]。由于数据流是时间序列，具有一次读取、持续处理、存储有限的特点，一般在滑动时间窗内对其进行分析。但是发动机故障发生的时机是不确定的，造成故障在时间窗内的位置也是不确定的。这说明同一故障模式样本的稀疏编码也需要考虑其位置信息。

Smith[8]在《自然》杂志上发表了移不变稀疏编码算法（Shift Invariant Sparse Coding，SISC）。该算法通过字典原子在时间窗范围的平移来匹配信号样本提高了稀疏编码的准确率，并具有出色的自适应性和鲁棒性等优点，有效解决了数据流的稀疏表示问题[9-10]。然而，字典原子的平移操作会降低整个编码模型的学习和解码效率，增加了发动机在线故障识别系统的计算复杂度，这对其运行实时性和计算资源成本构成了压力。Tang H等[11]采用基于梯度优化的字典学习算法，在改善学习效率的同时也牺牲了一定的精度。

本文在已有SRC和SISC理论的基础上，提出了一种快速移不变稀疏分类算法（Fast Sparse Representations Classification，FSRC）。该算法通过特征标记法和拉格朗日对偶法对移不变稀疏编码问题进行快速求解，在保证精度的前提下提高了模型的学习速度和实时性能。通过使用FSRC算法对汽油发动机中几种机械故障进行在线识别，来验证其实际的运行性能。

1 基础理论

1.1 SRC算法

SRC直接使用训练样本集S={sm×1}来构造冗余的分类字典 Dm×n=[D1,D2,…,DC],m≪n，其中C为类别数，Di是由第i个类别的样本构成的子字典。基于样本只能由所属同类子字典中的原子进行线性表出的假设，分类问题可以通过以下步骤来实现：

（1）对于测试样本t，求解式（1）的优化问题以获得其在分类字典D上的稀疏编码：

其中，s为样本t的稀疏表示系数向量，β为惩罚因子。

（2）用向量s在字典D上重构样本t，并根据最小重构误差进行分类：

其中，si是S中对应第i个分类的非零系数。

1.2 SISC算法

SISC是SRC算法在时域上的扩展。样本tm×1可以按式（3）进行表示：

其中，Tl是让字典 Dm×n中的原子di偏移l的平移操作，l∈[-L,L]，si,l是与产生偏移l的原子di相对应的稀疏表示系数，μ是服从高斯分布的误差。也就是说，SISC算法通过让字典原子在整个信号范围内进行平移来提高模型对数据流信号的匹配效果。

针对样本集T={tk}k=1,2,…,K的移不变稀疏编码求解问题可表达为：

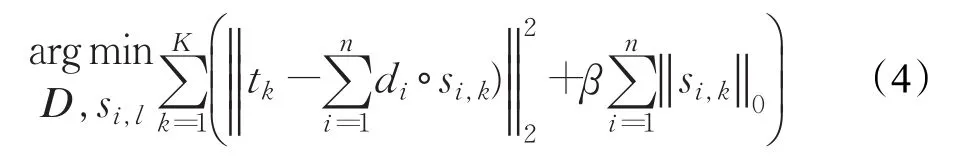
其中，si,k为信号tk在原子di上的稀疏表示系数，∘为卷积运算符。由于式（4）是非凸优化问题，所以一般通过反复迭代法分别对D和si,l进行求解。即先固定si,l后求解D，再固定D后求解si,l，重复这个过程直到满足停止条件。

2 快速稀疏系数求解算法

2.1 算法原理

稀疏表示系数s的求解是在固定字典D的前提下进行的，也就是将式（4）转换为：

鉴于卷积在时频域上的计算特性，可将式（5）变换到频域中进行求解[12]：

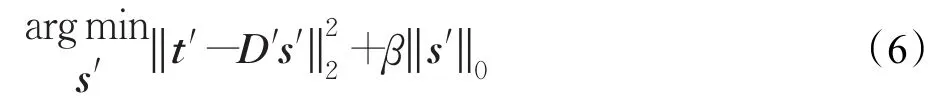
式（6）的常见解法主要有基追踪法（BP）、正交匹配法（OMP）[13]等贪婪迭代法。为了进一步提高效率，本文基于特征标记法[14]进行求解。该算法通过对稀疏表示系数向量中的元素进行标记，有选择地迭代更新稀疏表示系数的子集，有效降低了整个求解过程的计算量，其具体步骤如下：

步骤1初始化s′和其对应的标记向量θ为零向量，活动集A=∅。

步骤2

步骤3设D′sub是D′中与活动集A中元素对应的原子组成的子字典，s′sub和θsub分别是s′和θ中与活动集A相对应的元素组成的子向量。采用凸二次规划算法对式（8）进行求解：

可得s′sub的更新结果为：

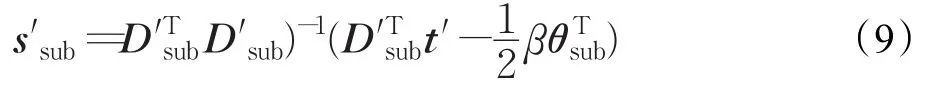
在s′sub更新前后的差值范围内搜索标记发生变化的元素，然后从活动集A中移除0元素并更新s′的特征标记θ =sign(s′)。

步骤4

步骤5对s′进行傅里叶逆变换获得稀疏系数s。

2.2 算法实时性能分析

OMP算法每次迭代都需要在所有原子上进行投影计算，其时间复杂度为O(kmn)（k为稀疏度，m为测量次数，n为样本维度）[15]。BP算法把式（6）的L0范数问题转化为L1范数问题，一般可以找到全局最优解，但其计算复杂度要高于OMP[15]。FSRC的稀疏系数求解算法依据活动集对稀疏表示系数中的非零元素进行标记。通过对子集s′sub的迭代更新，完成s′的求解，其时间复杂度仅为O(km×lbn)。此外，该在线求解算法只需要在迭代算法所需空间的基础上再增加n个单元来存储活动集A，其空间复杂度为O(n)。这对于目前的车载处理器来说并不会构成负担。

3 快速字典学习算法

3.1 算法原理

在固定稀疏系数的情况下对字典进行学习，即对以下问题进行求解：

但直接求解式（10）的计算量较大，需要进行优化处理。为了计算方便，同样需要将其变换到频域进行求解。则式（10）所述问题可转换为：

其中，T′={t′k}，S={s′i,k}，D′={d′i}。 t′k、s′i,k和 d′i分别是tk、si,k和di的傅里叶变换，c为一常数。式（11）是一个典型的约束最小二乘优化问题，一般直接采用梯度下降法进行求解，但其求解速度要受到迭代次数的影响。为了提高求解速度，本文基于拉格朗日对偶法进行求解。

设式（11）的拉格朗日目标函数为：

其中，λj＞0为对偶变量。其拉格朗日对偶问题为：

其中，φ=diag(λ)。则 Du()λ的梯度为：

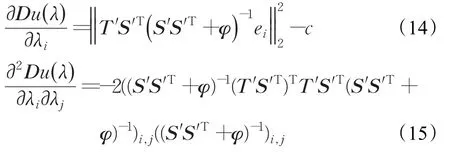
其中，ei∈Rn是第i个单位向量。可以采用共轭梯度法等直接对式（13）进行求解。

对Du(λ)最大化后，就可以得到最优字典D′为：

接着对D′进行傅里叶逆变换即可获得最优字典D。

3.2 算法性能分析

由式（12）和式（16）可知，字典 D′的学习过程实际上就是n个对偶变量λ的求解过程。也就是说，上述基于对偶求解的字典学习算法平均只需要优化n规模的数据量即可完成对m×n字典的优化。而传统基于梯度下降法的字典学习算法需要处理m×n规模的数据量。

4 故障识别算法

基于上述讨论，本文设计了一种能够对汽油发动机故障进行在线快速识别的算法（FSRC）。该算法基于SRC算法框架对发动机工况数据流的故障模式进行识别。考虑到故障发生时刻的不确定性，采用SISI算法对数据流进行移不变稀疏编码。通过字典原子与对应稀疏表示系数的卷积操作来提高编码效率。整个FSRC算法分为离线训练和在线识别两部分。其中离线部分的主要任务是学习分类字典，其中每个分类子字典由同类故障样本进行训练。在线部分的任务是在学习完成的字典上求取稀疏表达系数并完成分类，其结构如图1所示。

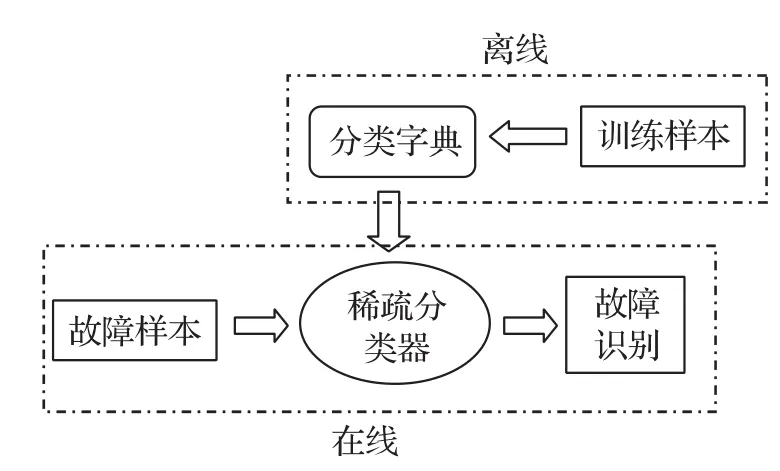
图1 FSRC算法结构示意图

FSRC算法的具体实现步骤如下：

（1）初始化分类字典以及算法参数；

（2）用第2章的算法求稀疏表示系数；

（3）用第3章的算法学习字典；

（4）反复运行步骤（2）～（4）直到满足停止条件；

（5）在学习获得的模型上对故障样本进行稀疏分类，实现故障类型的识别。

5 实验与讨论

5.1 实验环境

实验对象采用长安福特2013款嘉年华手动时尚型配备的1.5 L Duratec型发动机。数据流样本通过诊断仪（VCM）从OBD接口直接采集，如图2所示。

图2 样本采集方法示意图

采用人工设置方法来模拟五种故障，分别有真空管漏气（VLF）、一缸喷油器堵塞无法全开（ISF）、EGR阀漏气（ELF）、进气计量孔堵塞（MAFS）和节气门卡滞（TSF）。表1所示的是发动机处于正常状态和故障状态下所采集样本的数量。

表1 发动机数据流实验样本

所有数据流的采样频率为20 Hz，采样时间为35 s。每一组数据流样本包含发动机转速信号（rpm）、负荷量（load）、油门踏板位置信号（ap）、节气门位置信号（tp）、进气流量信号（maf）、点火提前角（adv）和短期燃油修正值（STFT），形成了一个7维向量。图3所示的是所采集的一组VLF故障的数据流样本。

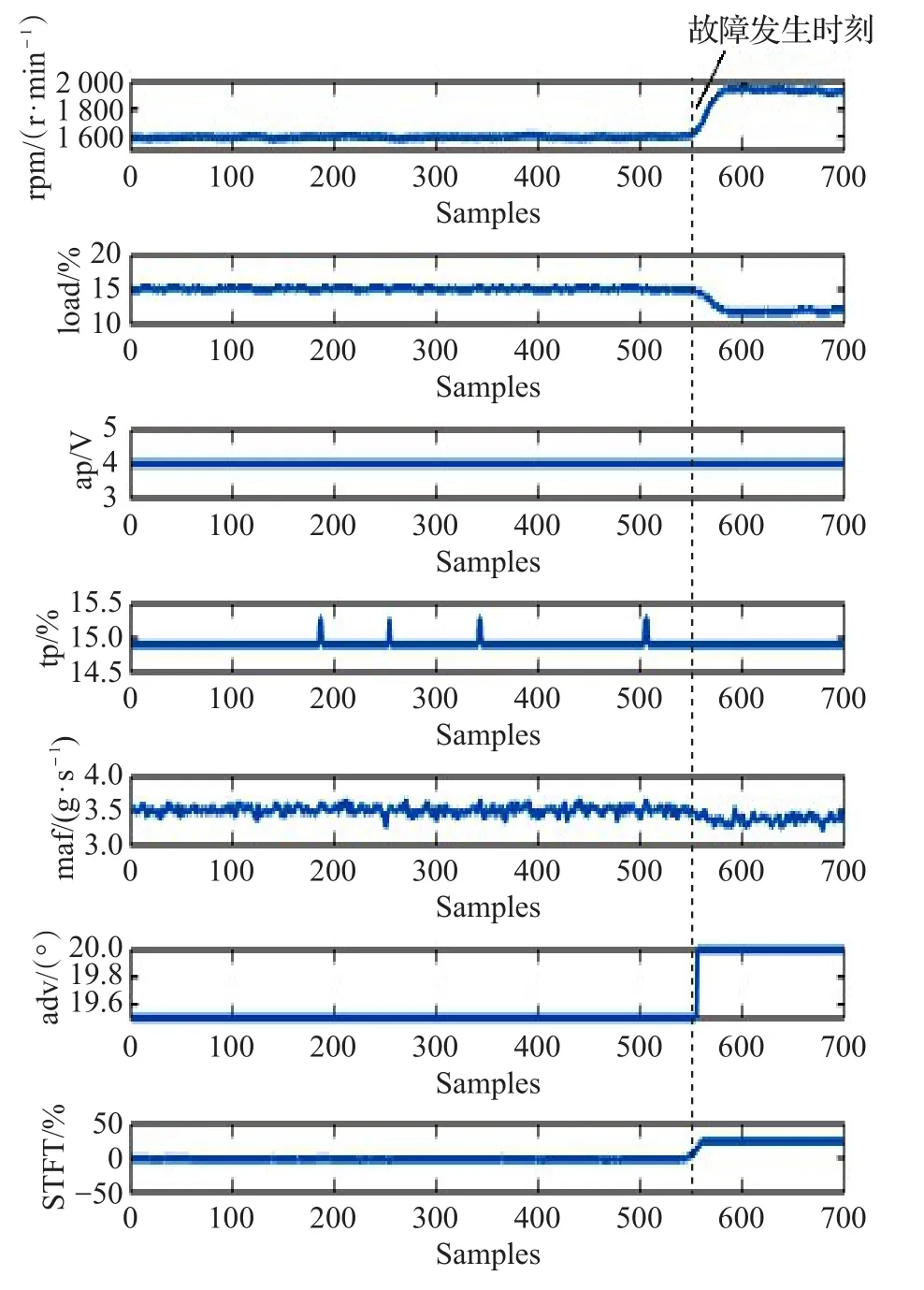
图3 VLF数据流样本

发动机的工作状态会受到负荷、外界环境、驾驶行为等因素的影响，所以其各个工况参数的变化幅度很大。此外，在采集相同故障类型的样本时，发动机工况参数也会发生变化。这意味着直接以原始数据流作为故障识别系统的输入样本难以获得理想的效果。因此有必要根据故障机理在原始样本基础上提取故障特征样本。本文中每个故障样本包含10个特征，包括rpm、tp和adv的能量；ap、maf、adv和STFT的均值；rpm和load的相关系数、rpm 和maf的相关系数、rpm 和tp的相关系数。上述特征都在滑动窗范围内求得，其模型如图4所示。

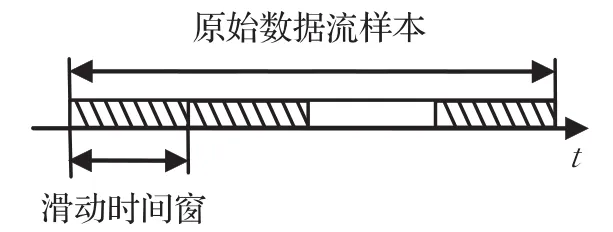
图4 滑动窗模型示意图

由于发动机发生故障后闭环系统会对故障进行修正，所以滑动窗的宽度不能太大，以免故障特征被掩盖。设每个滑动窗的宽度都为35个样本点，则字典原子的偏移范围为20。

5.2 实验结果与分析

对特征样本进行归一化后作为FSRC算法的输入样本。分类字典为10×120的矩阵，其中包含6个分类子字典 D1,D2,…,D6，分别对应无故障、VLF、ISF、ELF、MAFS和TSF共6种状态，每个子字典的规模相同，都为10×20。设惩罚因子β=0.1，终止条件为1E-5。

根据10折交叉验证法将所采集的全部1 080组样本按照9∶1的比例随机分成训练样本集和验证样本集两类。在其上共进行10次实验，以考察FSRC算法模型的识别效率和平均训练时间。同时和基于SISC的稀疏分类算法（SSRC）、基于OMP的稀疏分类算法（OSRC）以及梯度下降的稀疏分类算法（GSRC）进行比较。所有算法在Matlab2010b上运行，处理器为Intel i5 3210M，内存4 GB。

表2所示的是三种算法在各个时间窗内对样本数据流进行移不变稀疏分类求解的平均时间。

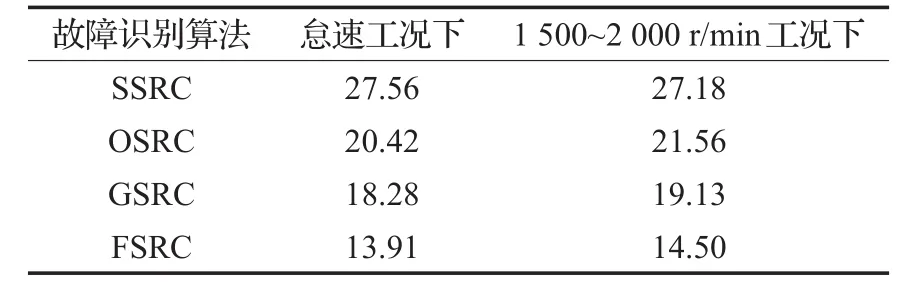
表2 各算法的平均在线分类时间 ms

可以看到，基于传统移不变稀疏分类的SSRC算法的时间复杂度最高，而FSRC算法的在线求解速度明显优于其他三种算法，这能够明显提高车载在线故障识别系统的运行效率。表3所示为各算法在相同样本上的平均训练时间。

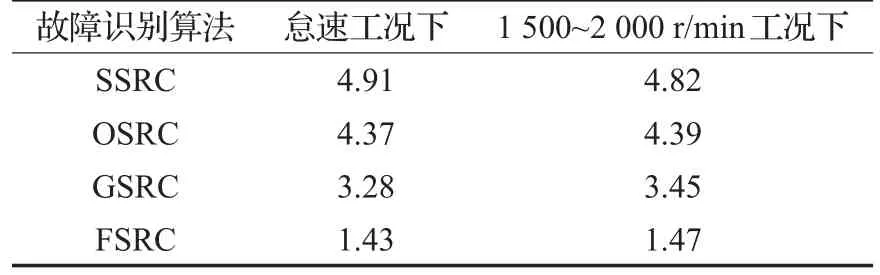
表3 各算法的平均训练时间s

由表3可知FSRC算法的训练速度是其他三种算法的2～3倍。图5所示的是一次故障识别过程中某个ISF故障特征样本在分类字典上的投影分布结果。

图5 稀疏表达系数在字典上的投影分布

从图5中可以看到，该样本在D3子字典上的稀疏投影系数值最大，说明其与该字典中原子的匹配度最好，这与事实是相符的。表4所示的是三种故障识别算法的平均识别精度。

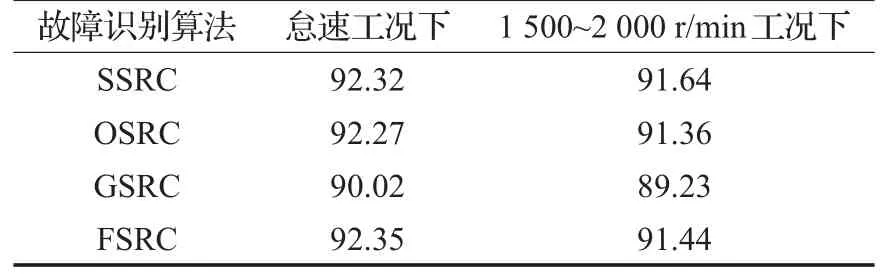
表4 各算法的平均识别精度 %

显然，FSRC的识别精度和其他三种算法相当。这表明FSRC没有因为学习效率的提高而牺牲故障识别的准确率。此外，注意到上述算法在怠速工况下的识别精度略高于1 500～2 000 r/min工况下，这是因为上述五种故障在怠速下的特征比发动机中速运行时要明显一些。

6 结束语

本文提出了一种基于快速移不变稀疏编码和稀疏分类的汽油发动机故障在线识别算法（FSRC）。该算法首先将移不变优化问题转换到频域上进行处理，接着分别通过特征标记法降低求解稀疏表示系数的计算量，拉格朗日对偶法代替传统的梯度下降法对字典进行快速优化。通过循环迭代逐渐逼近最优的稀疏系数和分类字典。将学习所得稀疏编码模型用于在线识别汽油发动机故障。对长安福特嘉年华1.5 L Duratec型发动机的五种常见机械故障进行在线识别的实验结果表明，FSRC算法在怠速和1 500～2 000 r/min工况下都取得了更快的在线稀疏求解速度，而且其在线识别精度没有受到任何影响，这表明其具有较好的应用前景。

参考文献：

[1]周东华，刘洋，何潇.闭环系统故障诊断技术综述[J].自动化学报，2013，39（11）：1933-1943.

[2]李哲洙，高培鑫，佟琨，等.基于HHT的液压管路裂纹故障诊断方法研究[J].计算机工程与应用，2016，52（20）：221-226.

[3]Wright J，Yang A Y，Ganesh A.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis&Machine Intelligence，2009，31（2）：210-227.

[4]Scholkopf B，Platt J，Hofmann T.Sparse representation for signal classification[C]//Conf on Advances in Neural Information Processing Systems，2006.

[5]Zhang Baochang，Perina A，Murino V，et al.Sparse representation classification with manifold constraints transfer[C]//The IEEE Conference on Computer Vision and Pattern Recognition（CVPR），2015：4557-4565.

[6]马小虎，谭延琪.基于鉴别稀疏保持嵌入的人脸识别算法[J].自动化学报，2014（1）.

[7]Plenge，Klein S，Niessen，et al.Multiple sparse representations classification[J].Plos One，2015，10（7）.

[8]Smith E C，Lewicki M S.Efficeient audiotory coding[J].Nature，2006，439（7079）：978-982.

[9]Liu H，Liu C，Huang Y.Adaptive feature extraction using sparse coding for machinery fault diagnosis[J].Machanical Systems and Signal Processing，2011，25（2）：558-574.

[10]Blumensath T，Davies M.Sparse and shift-invariant representations of music[J].IEEE Transactions on Audio，Speech and Language Processing，2006，14（1）：50-57.

[11]Tang H，Chen J，Dong G.Sparse representation based latent components analysis for machinery weak fault detection[J].Mechanical Systems and Signal Processing，2014，46（2）：373-388.

[12]Grosse R，Raina R，Kwong H.Shift-invariant sparse coding for audio classification[C]//Conference on Uncertainty in AI，2007：149-158.

[13]Needell D，Vershynin R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J].Foundations of Computational Mathematics，2007，9（3）：317-334.

[14]Lee H，Battle A，Raina R，et al.Efficient sparse coding algorithms[J].Advances in Neural Information Processing Systems，2006，19：801-808.

[15]孙林慧，杨震.语音压缩感知研究进展与展望[J].数据采集与处理，2015，30（2）：275-288.