改进量子粒子群算法的模糊神经网络水质评价

彭越兮，徐蔚鸿，2，陈沅涛，马宏华

PENG Yuexi1,XU Weihong1，2,CHEN Yuantao1,MAHonghua3

1.长沙理工大学 计算机与通信工程学院，长沙 410114

2.南京理工大学 计算机科学与工程学院，南京 210094

3.湖南省资兴市科学技术局，湖南 郴州 423400

1.School of Computer&Communication Engineering,Changsha University of Science and Technology,Changsha 410114,China

2.School of Computer Science&Engineering,Nanjing University of Science&Technology,Nanjing 210094,China

3.Zixing Muncipal Bureau of Science and Technology of Hunan Province,Chenzhou,Hunan 423400,China

1 引言

水质评价是通过对水体各项生物指标的检测和调查，根据不同的目的使用一定的方法对水体质量的优劣作出清晰的定量描述。评价的目的是为了获取水体的污染程度，并通过评价结果对水体划分水质等级，为水体的科学管理和污染防治提供依据。在过去的几十年中，在水质评价领域内已经有了许多研究工作[1-2]，水质评价的方法主要有指数评价法、模糊综合评价法、灰色评价法以及人工神经网络评价法等，评价的方法由线性转向非线性，主观性转向客观性，这反映了水质数据评价中参数的不确定性。人工神经网络（Artificial Neural Network，ANN）是一种处理复杂非线性问题的有效方法，近年来，随着ANN的蓬勃发展，许多研究者将其应用于日常的水质评价中[3-4]，并取得了不错的效果。但是，ANN评价法也存在一些缺点，比如计算时间长、收敛慢、容易陷入局部最小值等。因此，许多研究者开发了使用诸如粒子群（Particle Swarm Optimization，PSO）算法优化ANN，以此改变ANN模型的性能[5-8]。T-S模糊神经网络（Takagi-Sugeno Fuzzy Neural Network，TSFNN）是模糊逻辑与神经网络的有机结合，可以处理具有强非线性或高度不确定的复杂问题[9-10]。此外，根据许多复杂基准函数的模拟结果表明，量子粒子群算法（Quantum-behaved Particle Swarm Optimization，QPSO）具有比基本PSO更好的全局搜索能力[11]。本文在QPSO的基础上，针对基本QPSO算法不能自适应调整收缩扩张系数β的值，提出了一种自适应QPSO算法（Adaptive Quantum-behaved Particle Swarm Optimization，AQPSO），从而改进QPSO算法的性能。

利用PSO算法优化神经网络进行水文方面的研究已有了不少成果，Gao等人利用PSO优化BP神经网络进行水质的预测，提高了预测的精度[12]。Taormina通过利用新的多目标PSO算法来训练河流水体模型，改进了以往利用PSO算法的神经网络河流预测模型的泛化能力[13]。Cheng等人提出了利用QPSO-ANN模型来对水库日常流量进行评估，实验结果表明，该方法比基本ANN模型具有更好的评估精度[14]。因此，为了更为提高模糊神经网络的泛化能力和计算效率，本文采用混合方法，耦合模糊神经网络和AQPSO算法，提出利用AQPSO算法作为T-S模糊神经网络的训练算法以提高水质评价的效率。

2 量子粒子群算法及其改进

2.1 基本粒子群算法

粒子群算法是由Kennedy和Eberhart于1995年提出的一种新的进化算法。在PSO算法中，首先初始化一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子会通过跟踪个体最佳值Pi和全局最佳值Pg两个极值来不断更新自己的位置与速度。假设在一个D维的搜索空间中，种群由N个粒子构成，每个粒子代表D维中的一个位置，其中第i(i=1,2,…,N)个粒子所处的位置为Xi，其速度为Vi，粒子的个体最佳位置为Pi={pi1,pi2,…,piD}，种群的全局最佳位置表示为Pg={pg1,pg2,…,pgD}，粒子i的速度与位置更新公式表示为：

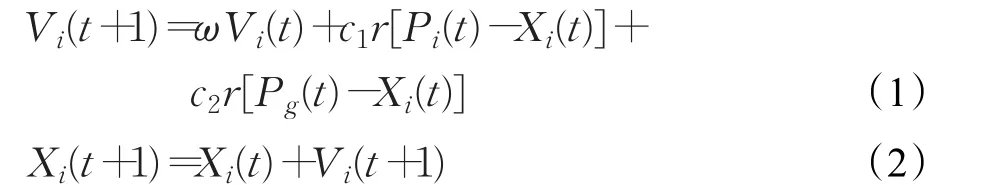
式中Vi(t),Xi(t)分别为粒子i在t时刻的速度与位置，c1，c2是学习因子，它们提供最优选择的功能。r为（0，1）之间的某一随机数。ω称为惯性权重。

2.2 量子粒子群算法

受到量子力学的启发，2004年，Sun从量子力学的角度上提出了量子粒子群算法。QPSO认为粒子拥有量子行为，不能根据不确定性原理同时确定位置矢量和速度矢量的精确值，因此，在QPSO中的粒子没有速度矢量，而是通过波函数ψ(x,t)来描述粒子的状态，并通过求解薛定谔方程得到粒子在空间中的某一点出现的概率密度函数，最后再利用蒙特卡洛随机模拟的方式得到粒子的位置方程：

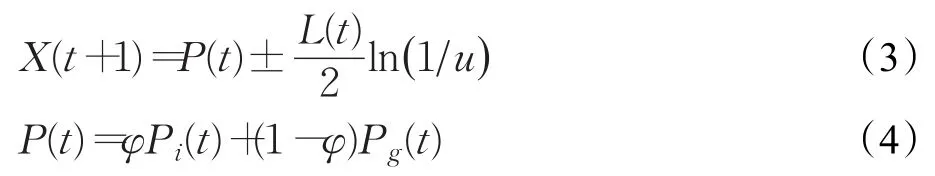
其中u和φ均是在[0，1]内变化的随机数，Pi(t)是粒子在迭代t次中的个体最佳位置，Pg(t)是t次迭代中整个群体的最佳位置。L的定义为：

其中，β为收缩扩张系数，N为粒子的总数目，D为粒子的维数，Pi是第i个粒子的个体最佳位置。最后得到的粒子位置方程为：

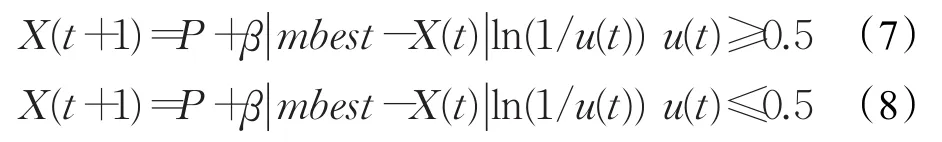
2.3 自适应量子粒子群算法

在QPSO算法中，算法无论是早熟收敛还是全局收敛，粒子群中的粒子都会出现聚集的现象，它们总是聚集在某一特定位置，或者某几个特定位置。因此，影响算法收敛性能的一个重要因素就是它们的聚集度。假设在一个极小值寻优的优化问题中，得出下式：

其中，avgPi(t)是所有粒子个体极值的平均值，Pg(t)是当前粒子的全局极值。可以得出，0＜g(t)≤1，当g(t)的值越大，粒子的聚集程度也会变大，而粒子的多样性则会越小，反之，聚集程度越小，则多样性越大。当g(t)=1时，粒子群中的所有粒子具有同一性，所有粒子将会聚集在一个点上。

收缩扩张系数β的选择对于QPSO算法非常重要，它对整个算法的全局和局部搜索能力、收敛速度与精度都有着一定的影响。β的值越大越有利于全局搜索，此时算法的收敛速度快，但不易得到精确的解，β的值越小越有利于局部搜索，可以得到精确的解，但是算法的收敛速度慢[15]。传统的QPSO中β的值一般按照下式取值：

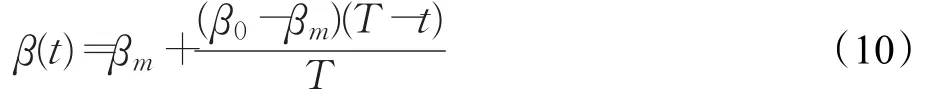
其中，β0和βm分别为收缩扩张系数的初值和终值。对于大多数的问题来说，β的值从搜索开始的1.0到终值0.5时，QPSO算法具有较优的性能。

在算法初期阶段，由于粒子的全局极值和粒子的历史个体极值差距比较大，此时需要较大速度全局搜索，以便于迅速接近全局极值，故此时收缩扩张系数的值应当处在较大的位置。而在算法进化后期，在粒子历史个体极值接近于全局极值后，则应减慢速度以加强算法的局部搜索能力，因此收缩扩张系数的值需适当减小，来提高算法的精确度。根据上述规律，本文提出了一种新的AQPSO算法，新算法将根据高斯曲线的规律和聚集度g(t)的变化，自适应调整收缩扩张系数β的值，新的β公式为：

从公式（8）、（10）可以看出，在算法迭代前期由于粒子聚集程度小，Pi和Pg的值差距会比较大，因此g(t)的值会比较小，β将处在一个较高的值。而到了迭代后期，粒子聚集度将变大，Pi和Pg的值差距会变得接近，g(t)的值会增大，所以β的值将会变小。

收缩扩张系数的变化情况如图1所示。

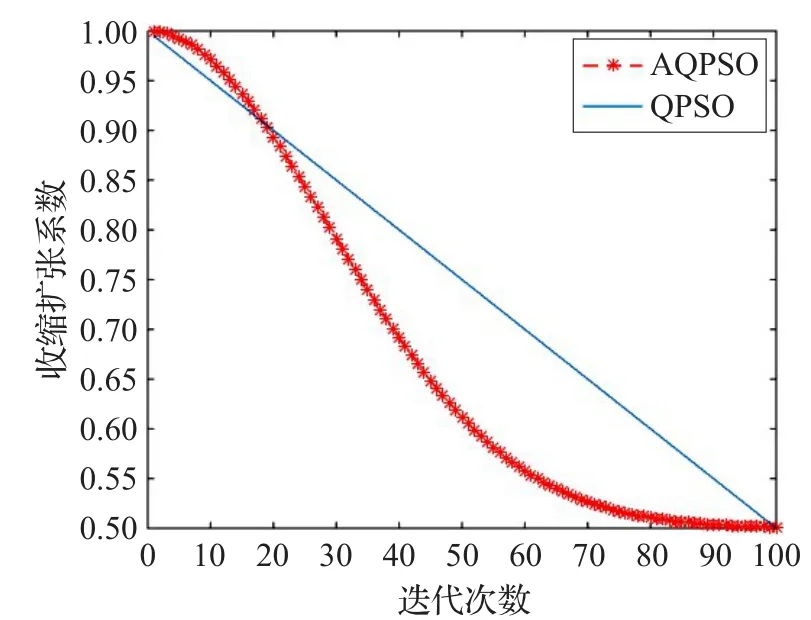
图1 收缩扩张系数的变化情况

3 基于AQPSO算法的T-S模糊神经网络模型

3.1 T-S模糊神经网络

T-S模糊神经网络是一种自适应能力很强的模糊系统，该神经网络不仅可以自动更新，而且还可以不断地自己修正模糊子集的隶属函数。用“if-then”规则形式来描述T-S神经网络的模糊推理如下：

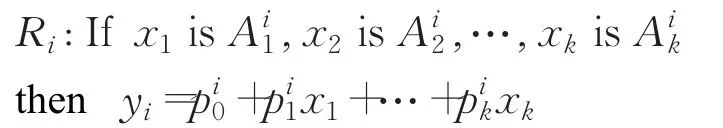
可以理解为在模糊规则Ri中，输入量（if部分）部分是模糊的，而输出部分（then部分）是根据模糊规则得到的确定值yi。可以看到，该模糊推理的输出结果是由输入的线性组合来表示的。其中和(j=1,2,…,k)分别是模糊系统中的模糊集和模糊系统参数，是第0个节点，它的输入值为x0=1，它将会提供输出部分中的常数项。

T-S模糊神经网络一般分为四层，第一层是输入层，将输入信息量x=[x1,x2,…,xk]T传输进入下一层，该层的节点数与输入参数的维数k相同。

第二层是模糊化层，该层的作用是计算各个输入分量属于各自语言变量值模糊集合的隶属度，隶属度函数一般采用高斯函数：

其中，是隶属函数的中心，是隶属函数的宽度。k是输入参数的维数，n是模糊子集数。

第三层是模糊规则计算层，该层将各隶属度进行模糊计算，计算出每条模糊规则的适应度，适应度计算采用连乘算子：

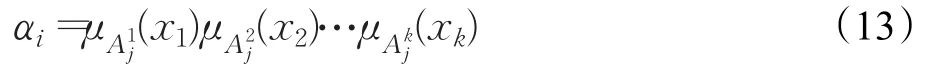
然后再对所有求得的适应度进行归一化计算：

最后一层是输出层，它会根据所计算的结果求出模糊神经网络模型的最终输出值：

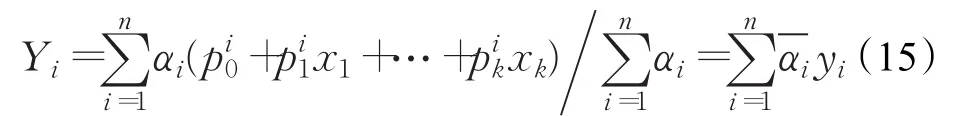
3.2 AQPSO-TSFNN的实现

为了获得更好的水质评价精度，本文尝试采用AQPSO算法对T-S模糊神经网络进行参数选择。在本文中，神经网络的输出层只有一个节点，为最后的水质评价值。如果输入层和隐层的节点数分别为n和m，则T-S模糊神经网络模型的结构为n-m-1。提出新模型的基本实现步骤描述如下：

（1）在 AQPSO算法中设置最大迭代次数T和种群粒子的数量N。将所有的数据分成训练集和测试集。在进行处理前，把所有的数据进行归一化，以确保评价结果的准确性。

（2）使用AQPSO算法对T-S模糊神经网络进行参数选择。将隶属函数的中心值和宽度，以及模糊神经网络的系数设置为AQPSO算法的初始位置。

（3）运行模型，并使用参数计算每个粒子的适应度。把这里的适应度设置为期望结果和输出结果之间的均方误差（Mean Square Error，MSE）。

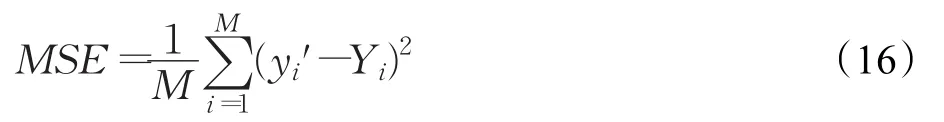
其中和Yi分别代表期望结果和输出结果，M是指所有样本的和。

（4）运行每个粒子的个体极值Pi和全局极值Pg。根据公式（5）和（10）分别计算平均粒子个体最佳值mbest和收缩扩张系数β。

（5）计算每个训练样本的输出值，直至达到最大迭代次数T或者最小训练误差。将训练后的T-S模糊神经网络参数应用于测试过程中。

4 基于AQPSO算法的T-S模糊神经网络的水质评价

4.1 水质评价标准

水质的评价是根据所采集的水的样本值通过一定数学模型计算所确定的水质等级，水质评价目的是为了能够判断出采样水质量的等级，并以此为依据来给水源提供保护。分析水体水质的指标有很多项，综合考虑水质监测数据的分析，主要选取以下六项指标作为评价参数：氨氮、溶解氧、化学需氧量、高猛酸盐指数、总磷和总氮，各项指标数值对应水质等级如表1所示。

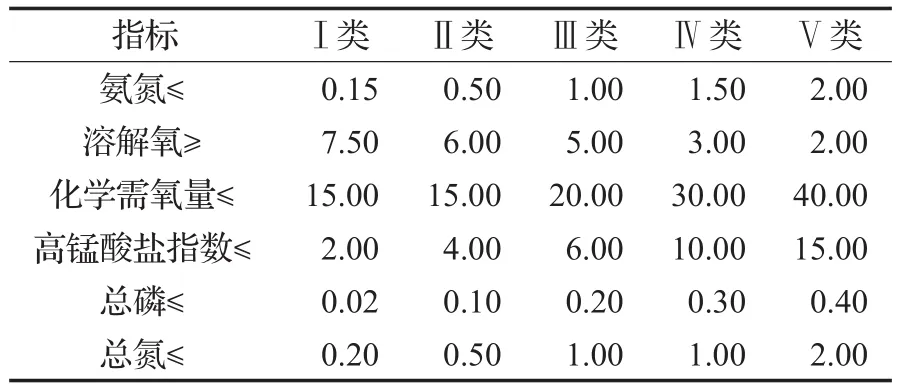
表1 地表水环境质量指标

模糊神经网络的输出结果所得的数值将规定在范围[0，5]内，可以根据得到的数值将其评判为水质中的某一类。表2为水质分类的评判标准。

表2 水质分类评判标准

4.2 实验数据及结果分析

本文的实验数据来源是湖南省资兴市东江湖流域2002年到2013年的环保水文数据，从2002—2007年的水文数据中选取400组数据来进行训练和测试，将其中350组数据作为神经网络模型的训练样本，另50组数据作为测试样本。在模型进行训练和测试之后，最后将东江湖流域的滁口、东坪、白廊3个水文监测站点2008—2013年6年共24组的数据通过模型来进行水质评价。表3是其中一个站点中的5组数据。

为了验证所提出的模型的有效性，对实验中所有的神经网络模型均使用相同的训练和测试样本，所有的神经网络结构均为6-12-1。设置粒子种群的规模N为40，最大迭代次数T为300次，最小训练误差条件设置为：当MSE到达10-4时，停止迭代。算法均在Matlab R2014b软件下实现结果。

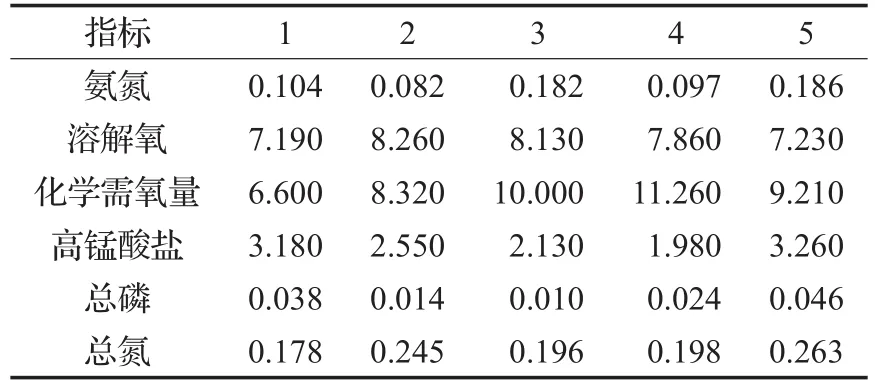
表3 数据样本

如表4和图2所示，AQPSO-TSFNN模型比其他四种神经网络模型的测试结果的MSE均要小，而且所用时间也要小于其他模型，通过训练和测试的实验可知，AQPSO-TSFNN模型的效率要大于其他四种神经网络模型。

表4 不同模型的测试结果

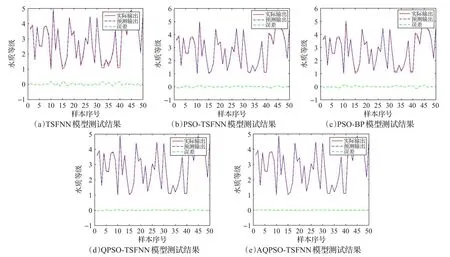
图2 样本测试结果

把滁口、东坪、白廊3个水文监测站点的24组数据通过训练和测试后的神经网络模型进行水质评价，结果如表5～9所示，可以看到，AQPSO-TSFNN的水质评价结果与实际检测的结果完全一致，而其他4个模型都出现了一定数量的评价误差。上述实验表明，对于水文站的水质评价，本文提出的AQPSO-TSFNN模型对比其他神经网络模型有着显著的改进，适合于做日常水质检测的工作。而且还可以得出结论，东江湖流域的水质在多年里保持在一个较高的水准，政府部门对于水质的保护措施做得十分得当，非常适合旅游或者水产养殖等项目开发。

5 结束语

水质的评价一直是水文工作站的一项重要检测项目，本文提出了一种新的AQPSO-TSFNN模型，该模型是基于新的自适应量子粒子群算法优化T-S模糊神经网络的参数的模型，并且将模型应用于日常的水质评价中，以帮助水文工作站点可以更为效率地进行日常的水

文数据分析。通过将新模型应用到东江湖流域的水文站点进行实验，结果表明，新的AQPSO-TSFNN比实验中其他神经网络模型的表现更具效率。因此，将新的AQPSO-TSFNN模型用于水文工作站中，可以帮助水文工作站更为效率地对当前水质进行评价，并作出处理手段。

表5TSFNN的评价结果

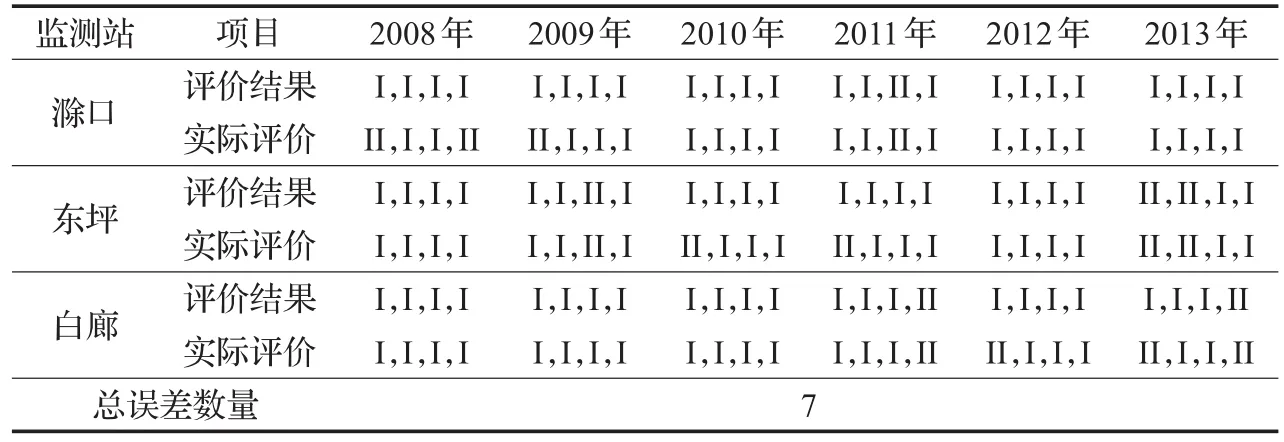
表6PSO-TSFNN的评价结果

表7 PSO-BP的评价结果

表8QPSO-TSFNN的评价结果

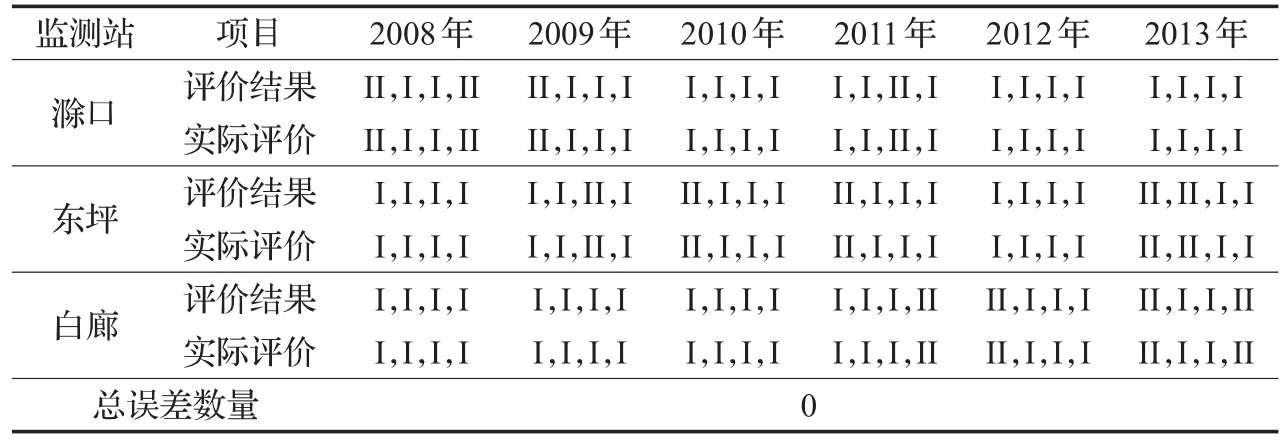
表9AQPSO-TSFNN的评价结果

参考文献：

[1]Simeonov V，Stefanov S，Tsakovski S.Environmetrical treatment of water quality survey data from Yantra River，bulgaria[J].Microchimica Acta，2000，134（1）：15-21.

[2]Lee H K，Oh K D，Park D H，et al.Fuzzy expert system to determine stream water quality classification from eco-logical information[J].Water Science&Technology，1997，36（12）：199-206.

[3]Zhou Zhongshou，Xu Lizhong.The application of fuzzy neural network based on T-S model in water quality evaluation[C]//Proceedings of 2007 IEEE International Symposium on Industrial Electronics，Centro Cultural and Centro Social Caixanova-Vigo，2007.

[4]Yuan Honglin，Gong Ling.Forecasting the water quality index in Zaohe River based on BP neural network model[J].Journal of Safety and Environment，2013，13（2）：106-110.

[5]Li Xuejun，Xu Jia，Zhu Erzhou，et al.A novel computation method for adaptive inertia weight of task scheduling algorithm[J].Journal of Computer Research and Development，2016，53（9）：1990-1999.

[6]Li Zuoyong，Wang Jiayang，Guo Chun.A new method of BP network optimized based on particle swarm optimization and simulation test[J].Acta Electronica Sinica，2008，36（11）：2224-2228.

[7]Jiang Jianguo，Ye Hua，Liu Huimin，et al.Particle swarm optimization method with combination of rapid information communication and local search[J].Journal of Harbin Engineering University，2015，36（5）：687-691.

[8]Asadnia M，Chua L H C，Qin X S，et al.Improved particle swarm optimization based artificial neural network for rainfall-runoff modeling[J].Hydrol Eng，2014，19：1320-1329.

[9]He Chunmei.The performance and research on the learning algorithms of fuzzy neural network[D].Nanjing University of Science and Technology，2010.

[10]Lin L，Guo F，Xie X，et al.Novel adaptive hybrid rule network based on TS fuzzy rules using an improved quantum-behaved particle swarm optimization[J].Neurocomputing，2015，149：1003-1013.

[11]Fang W，Sun J，Ding Y，et al.A review of quantumbehaved particle swarm optimization[J].Iete Technical Review，2010，27（4）：336-348.

[12]Gao Feng，Feng Minquan，Teng Sufen.Based on PSO optimized BP neural network of research on water quality prediction[J].Journal of Safety and Environment，2015，15（4）：338-341.

[13]Taormina R.Neural network river forecasting with multiobjective fully informed particle swarm optimization[J].Journal of Hydroinformatics，2014，17（1）：99-113.

[14]Cheng C T，Niu W J，Feng Z K，et al.Daily reservoir runoff forecasting method using artificial neural network based on quantum-behaved particle swarm optimization[J].Water，2015，7（8）：4232-4246.

[15]Sun J，Xu W，Feng B.Adaptive parameter control for quantum-behaved particle swarm optimization on individual level[C]//IEEE International Conference on Systems，Man and Cybernetics，2005：3049-3054.