求解高维优化问题的遗传鸡群优化算法

杨小健，徐小婷，李荣雨

YANG Xiaojian,XU Xiaoting,LI Rongyu

南京工业大学 计算机科学与技术学院，南京 211800

School of Computer Science and Technology,Nanjing University of Technology,Nanjing 211800,China

1 引言

群体智能（Swarm Intelligence，SI）作为一个新兴领域自从20世纪80年代以来引起了多个学科领域研究人员的关注，其中发展比较快的有生物、经济、人工智能、社会等学科领域，群体智能已经成为这些交叉学科研究的热点和前沿领域[1]。人们研究发现，在自然界中的有些群体当中单个个体没有很高的智能，但个体之间可以通过分工合作、相互协调，完成复杂的任务，最终表现出较高的智能。群体智能优化算法（Swarm Intelligence Algorithm，SIA），就是在此基础上利用数学方法抽象出数学模型并设计出的具有强大的问题求解能力的新型随机优化算法[2-3]。相对于传统算法，它具有自学习、自组织、自适应的特征和简单、通用、易懂、鲁棒性强、并行处理等优点，它在解决许多优化问题当中显示了强大的优越性[4-5]。例如遗传算法（Genetic Algorithm，GA）[6]、粒子群优化算法（Particle Swarm Optimization，PSO）[7-8]、萤火虫算法（Firefly Algorithm，FA）[9]、共生生物搜索算法（Symbiotic Organisms Search，SOS）[10]、布谷鸟算法（Cuckoo Algorithm，CA）[11-12]、蝙蝠算法（Bat Algorithm，BA）[13]等。以上列举的这些群体智能优化算法对于解决各领域复杂的优化问题提供了新的有效途径，成为当前研究的热点[14]。文献[15]刘天堂等人将遗传算法用于求解能力约束弧路径问题；文献[16]Yoshida H等人将粒子群算法用于电压控制以及电压安全评估方面；文献[17]Gandomi A H等人将萤火虫算法用于混合变量结构优化中；文献[18]XiaoLY等人将萤火虫算法用于电力负荷预测中；文献[19]Yang X S等人将布谷鸟搜索算法用于结构优化问题途径的求解中。同时新的群体智能优化算法仍在不断出现和发展过程中。

鸡群算法（Chicken Swarm Optimization，CSO）[20]是由Meng XB等人于2014年在第五届群体智能国际会议中提出的一种群体智能优化算法。和粒子群优化算法、差分进化算法[21等智能优化算法相比，该算法能够在全局范围内随机搜索，从而得到全局最优解的概率大大增加。这表明鸡群算法在求解全局最优问题时确实显示出一定的优越性，但是文献[20]只是在低维时（维数D=10）对基准测试函数进行了求解，它没有考虑高维的情况并作进一步的求解与分析。

本文首先求解出高维时(D=100)的实验数据，通过分析实验结果，发现算法出现了寻优精度降低、收敛速度变慢、偏离了全局最优的情况。针对这种不足，提出一种基于交叉、变异的遗传鸡群算法（Genetic Chicken Swarm Optimization，GCSO），该算法在标准鸡群算法的基础上，利用遗传算法的交叉、变异特性，增加公鸡和母鸡交配产生新小鸡的概念，根据设定的交配周期和小鸡淘汰更新周期，适应度函数值最差的那部分小鸡被及时淘汰掉，适应度函数值较好的小鸡则被保留下来，按照设定的交配周期和淘汰更新周期进行小鸡的迭代及判断。为了验证本文所提算法的可行性和优越性，实验求解了10组基准函数问题。实验结果表明，在高维情况下，该算法确实可以防止算法陷入局部最优，并改善了算法的收敛性能以及稳定性和鲁棒性。

2 鸡群算法（CSO）

2.1 算法介绍

CSO算法是根据自然界中鸡群的等级制度及分配原则建立的，它归纳为以下4点原则。

原则1一个鸡群包括若干子群，每个子群中包括一只公鸡、若干母鸡和小鸡。

原则2通过适应度函数值来建立等级制度并区分不同类型的鸡。在鸡群中，选取适应度函数值最差的若干个体作为小鸡，最好的若干个体作为公鸡，剩余的若干个体就作为母鸡；每个子群当中适应度函数值最好的个体作为公鸡，适应度函数值最差的那部分作为小鸡，母鸡随机选择子群，同时母鸡和小鸡之间的母子关系也是随机建立的。

原则3在每个子群中，等级制度、主导关系、母子关系是确定不变的，只有到达更新周期G时才会重新建立。

原则4在每个子群中，所有鸡跟随公鸡寻找食物，它们可以阻止其他鸡偷取自己的食物。假设，每只鸡可以随机偷取已经被其他鸡发现的食物，小鸡寻找自己母亲周围的食物，并且主导能力越强的那些鸡越有优势寻找到食物。

在CSO算法中，假设整个鸡群数量为N，最好的RN只被假定为是公鸡，它们可以在更广泛的空间寻找食物，最差的CN只被视为小鸡，其余的HN只被视为母鸡，MN只被视为可以生育小鸡的母鸡。通过适应度函数值 f来反映不同鸡的地位和竞争力。适应度函数值越好的个体代表地位更高，竞争力也越强，越会先得到食物。

根据等级制度及分配原则，可以确定公鸡、母鸡、小鸡的位置更新公式如下所示。

公鸡对应的位置更新公式为：

式（1）中，Randn(0 ,σ2)表示标准差为 σ2、均值为0的正态分布；ε为一个取值非常小，无限接近0的常数，主要用于避免误差；k表示在公鸡组随机选择的可以代表公鸡的指数；f表示x对应的适应度函数值。

母鸡对应的位置更新公式为：

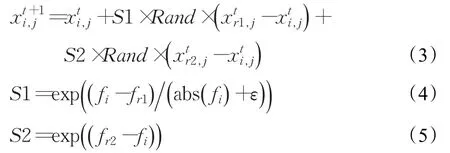
式（3）中，Rand表示在[0 ,1]均匀取值的随机数；r1∈[1 ,N ]，它表示与母鸡i对应的公鸡；r2∈[1 ,N]，表示鸡群中随机选取的公鸡或母鸡，且r1≠r2。

通过分析式（4）、（5），可以得出 S2＜1＜S1。假设S1=0，则母鸡i只跟随其他的鸡寻找食物；假设S2=0，则母鸡i只寻找自己领地范围内的食物。

小鸡对应的位置更新公式为：

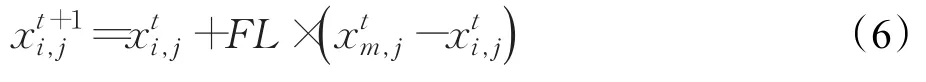
式（6）中，表示小鸡i母亲的位置；FL∈[0 ,2]，反映了小鸡跟随母亲寻找食物的本领。

2.2 CSO算法性能分析

CSO算法只是在低维(D=10)情况下求解与分析的，为了分析CSO算法在高维时的情况，文中选取了以往求解优化问题最常用的3组基准函数作为求解对象，在100维时进行了求解，并对比了GA和PSO两种优化算法。求解结果如表1所示。

通过表1，可以得出当高维时（D=100），CSO算法和GA算法以及PSO算法的实验结果对比没有像在低维时(D=10)那样明显的优势，基准函数Griewank和Rosenbrock的取值不理想。尤其是函数Rosenbrock的取值（粗体部分）已经明显偏离全局最优解，收敛精度大大降低，算法性能表现不佳。

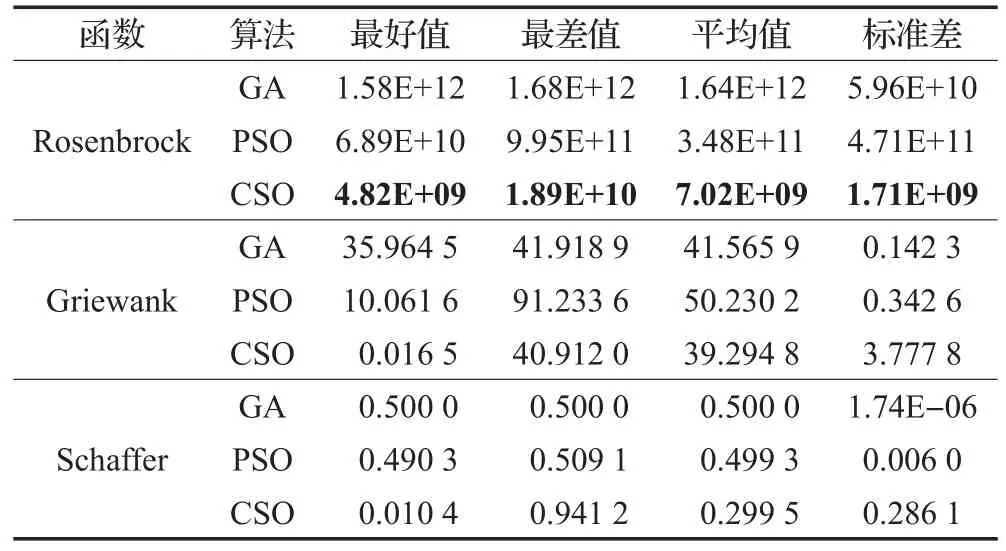
表1 3组基准函数在D=100时的实验结果

3 遗传鸡群算法

针对CSO算法存在的不足，本文提出一种基于交叉、变异的遗传鸡群优化算法（GCSO）。该算法的基本原理是：（1）引进交配周期（mating cycles），利用遗传算法的交叉、变异特性，增加公鸡和母鸡交配产生新小鸡的概念；通过交叉、变异过程得到新生小鸡，并根据设定的条件判断新生小鸡的性别。（2）引进小鸡淘汰更新周期（update cycles），淘汰更新率为0.1。这个过程中，适应度函数值最差的那部分（前10%）小鸡被淘汰掉，保留下来的小鸡继续充当新的小鸡角色。（3）引进平均错误率(AER)，以评估算法对每组基准函数的平均错误率。

3.1 公鸡、母鸡交配产生新小鸡以及新生小鸡淘汰更新过程

步骤1从所有公鸡组当中选择相应的基因片段，确定基因型，求解得到其适应度函数值 fit1；同理，从所有母鸡组当中选取相应的基因片段，确定基因型，求解得到其适应度函数值 fit2。

步骤2对选取的公鸡和母鸡基因片段进行重组（交叉率pc=0.8），得到新的公鸡和母鸡基因型。

步骤3判断是否发生基因突变（变异率pm=0.2），根据判断结果得到新的公鸡、母鸡基因型。根据新得到的公鸡、母鸡基因型，求解对应的适应度函数值 fit11、fit22。

步骤4比较 fit11、fit22和 fit1、fit2的大小。如果 fit11＜fit1、fit22＜fit2，则用 fit11和 fit22替代 fit1和 fit2，并将其作为新生小鸡基因，将小鸡基因型进行存储（孵化阶段）。

步骤5选择新出生小鸡的前10%进行更新，根据更新结果作出判断，最终淘汰适应度函数值差、有缺陷的小鸡。

根据GCSO算法的基本原理（3），平均错误率公式定义如下：

式（7）中，i∈[1,2,…,10]，取整数；g′为最优值的平均值，ki表示第i组基准函数对应的全局最优解。

3.2 GCSO算法的实现步骤

步骤1初始化鸡群，设置种群规模N、公鸡数量RN、母鸡数量HN、小鸡数量CN、鸡妈妈数量MN、更新周期G、交配周期mating cycles、小鸡淘汰更新周期update cycles、交叉算子 pc、变异算子 pm、最大迭代次数iterMAX、问题维度D等。

步骤2计算t=0时鸡群N的适应度函数值。

步骤3判断t%G=0是否成立，若成立，则根据适应度函数值在鸡群中建立等级制度。并根据等级制度把整个鸡群划分成若干个不同的子群，在每个子群中确立母鸡和小鸡之间的对应关系。

步骤4对于，判断i表示的对象，当i表示公鸡时，根据式（1）求解；当i表示母鸡时，根据式（3）求解；当i表示小鸡时，根据式（6）求解。

步骤5判断是否满足交配周期条件，若满足，则通过交配步骤得到新生小鸡。

步骤6判断是否满足淘汰更新周期条件，若满足，则对新生小鸡进行更新与淘汰。

步骤7计算新解的适应度函数值，并与当前最优解作比较，如果新解的适应度函数值优于当前最优解的，则用新解替代当前最优解。

步骤8判断是否满足迭代终止条件，如果满足则结束算法，输出求解结果；否则转到步骤3继续迭代和判断。

4 实验结果及分析

4.1 基准函数类型及参数设置

为了验证文中所提算法的可行性和有效性，实验通过对10组基准函数分别在维度D=20和D=100时进行求解，同时与GA、PSO、CSO三种算法进行对比。为了公平起见，所有的算法种群规模N为100，每种算法独立运行30次，仿真软件为matlab2014a，最大迭代次数iterMAX 为1 000。

实验时，选取的10组基准函数包括单模态和多模态两种情况。其中，F2、F7、F8、F9、F10为单模态；F1、F3、F4、F5、F6为多模态。通过对单模态和多模态两类函数的求解，得出的结果具有普遍性，可以更全面地反映文中各种算法的性能。10组基准函数类型如表2所示。四种算法的参数设置如表3所示。

4.2 对比实验及结果分析

实验通过求解10组基准函数的最好值、最差值、平均值、标准差来判断算法解的优劣。在相同目标条件之下，最好值和最差值反映了算法的取值情况；平均值反映了算法所能达到的求解精度；标准差反映了算法的稳定性和鲁棒性。10组基准函数分别在维度D=20和D=100时的求解结果如表4和表5所示。表中求解结果最好的值用粗体表示。

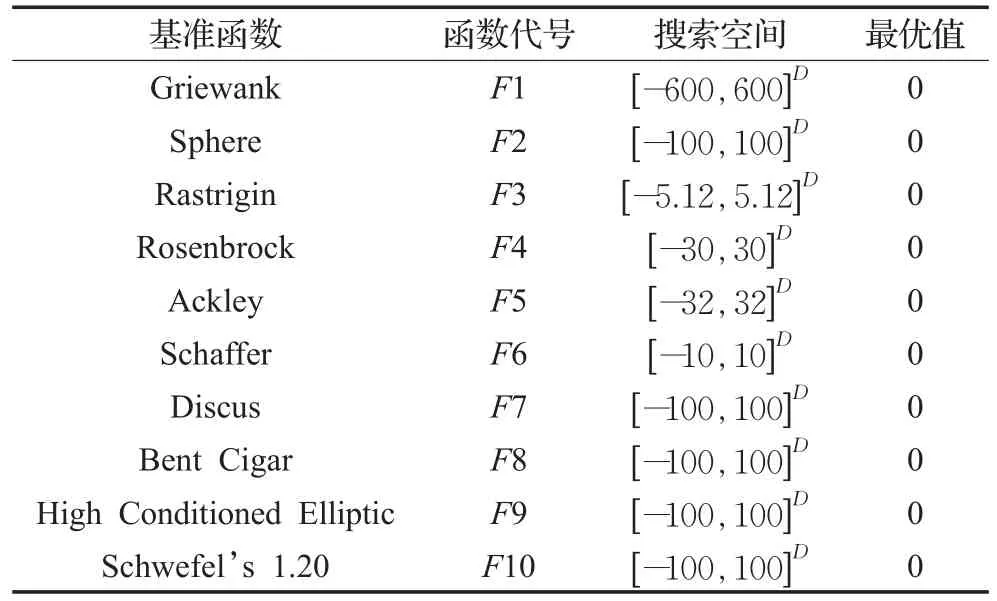
表2 基准函数

表3 四种算法的参数设置

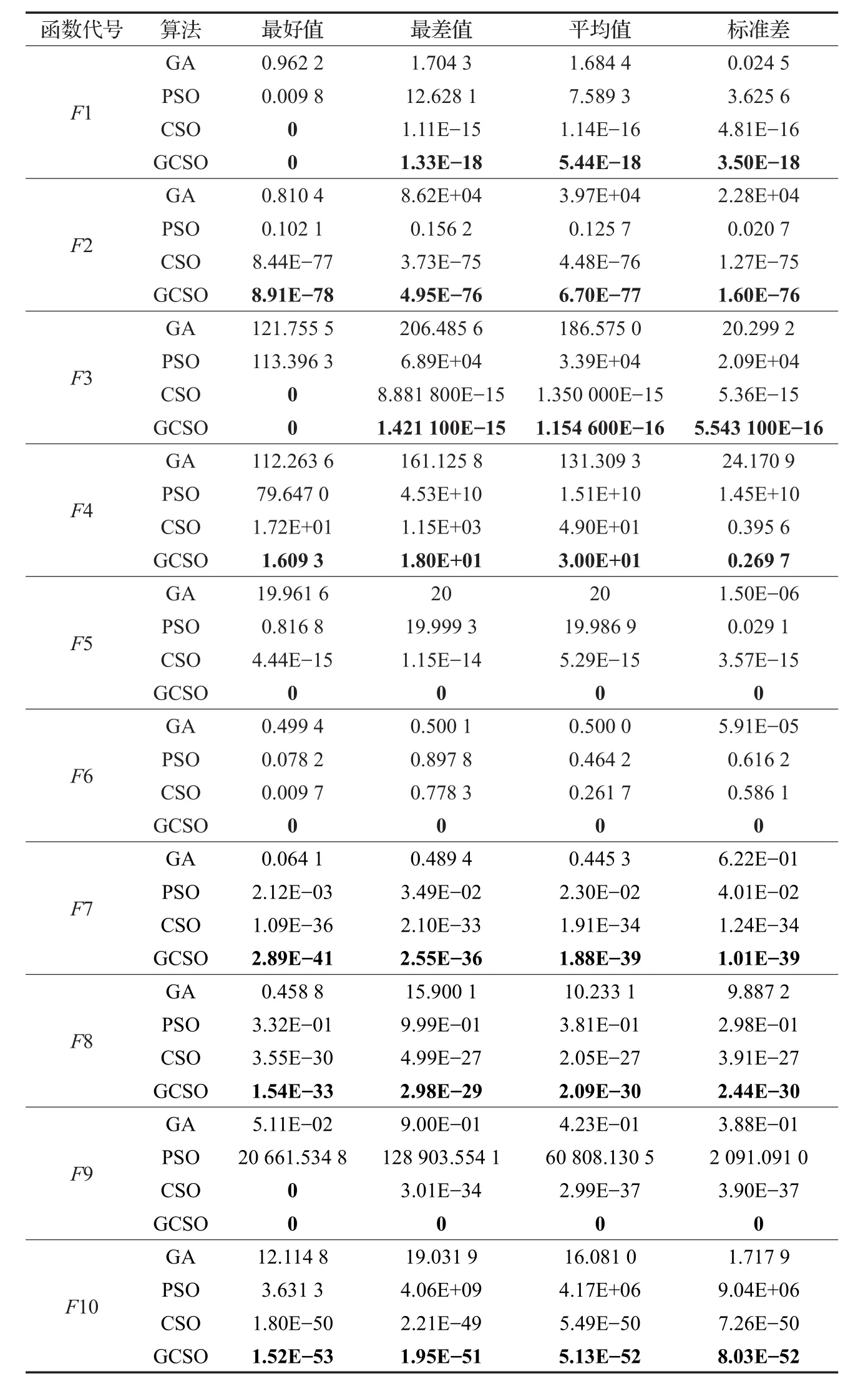
表4 10组基准函数在D=20时的实验结果

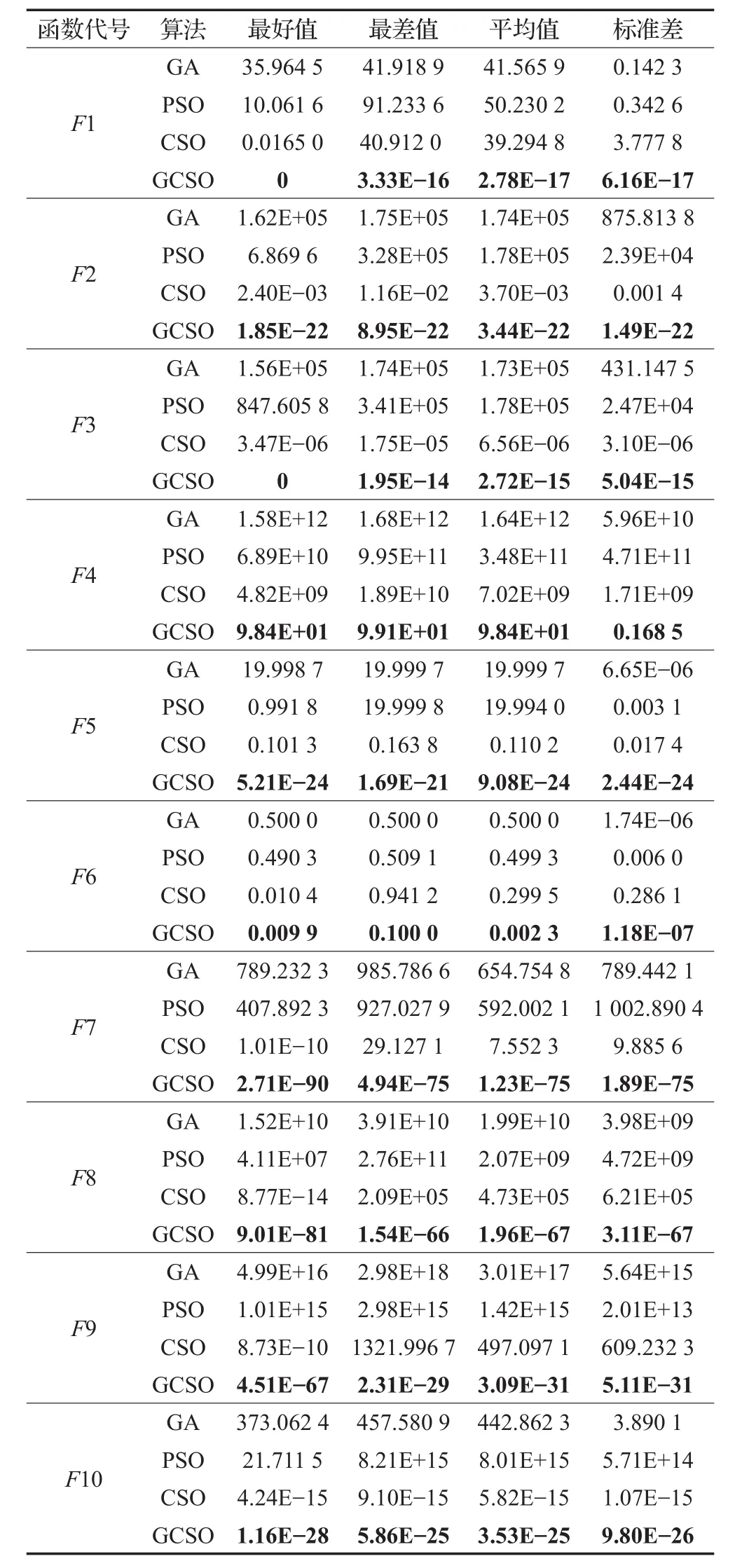
表5 10组基准函数在D=100时的实验结果

通过表4可以得到，在D=20时GCSO算法和CSO算法的实验结果远远优于GA算法和PSO算法的实验结果。进一步分析GCSO算法和CSO算法的实验结果，发现GCSO算法的实验结果均优于CSO算法的实验结果，尤其是对于基准函数F5、F6、F9，GCSO算法可以达到全局最优，而CSO算法却没有达到全局最优。

通过表5可以得到，D=100时CSO算法已经明显偏离全局最优，F1、F4、F7、F8、F9的求解结果显示其已经明显陷入局部最优，求解结果不理想。同时GCSO算法却能克服局部收敛并得到较好的结果，这从除F4之外的9组基准函数的实验结果均可体现出来。

综合表4和表5可以得到，在D=20和D=100时GCSO算法的求解结果均优于CSO算法的求解结果，且远远优于GA算法和PSO算法的求解结果。此外，由于平均值反映了算法所能达到的求解精度；标准差反映了算法的稳定性和鲁棒性。通过表4和表5也可得出GCSO的求解精度、稳定性以及鲁棒性优于CSO、PSO、GA这三种算法的。

为了反映10组基准函数在各种算法运行下的平均错误率，根据公式（7）得到的实验结果如表6所示。

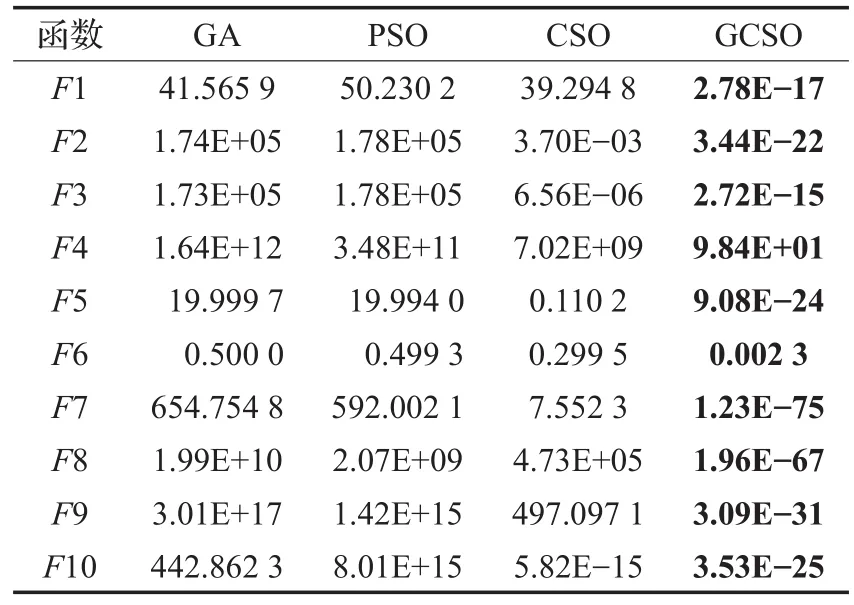
表6 10组基准函数的平均错误率

通过表6，可以得出GCSO算法的平均错误率最低。尤其在F1～F5、F7～F10这9组基准函数上和其他三种算法求解结果的数量级相差很大，区分度好。

为了更为直观地反映每种算法的寻优精度以及收敛速度。在D=100时，每种函数独立运行30次，得到在D=100时的函数收敛曲线图，如图1所示。

通过图1，可以看出GCSO算法的收敛精度和收敛速度均优于CSO算法，且远远优于PSO算法和GA算法的。这体现了GCSO算法在高维时，也能保持良好的性能。

4.3 算法复杂度分析

算法的复杂度评估主要包括空间复杂度和时间复杂度两方面。

空间复杂度是指算法在计算机内执行时所需要的最大存储空间的度量。文中四种算法的空间复杂度相当。时间复杂度是指一种算法执行时所消耗时间的度量。对于群体智能优化算法而言，时间复杂度正比于种群规模N和迭代次数t。通过分析，可以得出GA算法的时间复杂度为O(Nt)；PSO算法的时间复杂度为O(Nt)；CSO算法的时间复杂度为O(Nt)；GCSO算法的时间复杂度为O(2Nt)(O(Nt+Nt))。由于迭代次数很大(t=1 000)，所以时间复杂度主要取决于迭代次数t。GCSO算法的时间复杂度和其他三种算法相比，计算成本有所增加，但仍在可接受的范围之内。

图1 GA、PSO、CSO和GCSO对10组基准函数在D=100时的收敛曲线比较

5 结束语

开发能力和探索能力是影响算法性能的两大决定因素，如何把握两者之间的矛盾平衡一直是智能优化算法重点关注的方面。针对CSO算法在求解高维复杂优化问题时存在收敛速度慢、寻优精度不高、容易陷入局部最优等不足，本文提出一种GCSO算法。该算法是在CSO算法基础上增加公鸡和母鸡交配、变异产生新小鸡的概念，设定公鸡、母鸡交配周期和小鸡淘汰更新周期，并引入了交叉算子、变异算子以及衡量算法求解值和实际值之间误差的平均错误率AER。实验时和GA、PSO、CSO三种算法进行了对比。仿真实验分别从解的质量、平均错误率、寻优精度以及收敛速度等角度对各种算法进行了测试和验证。10组基准函数的仿真结果表明，文中提出的GCSO算法在寻优精度、平均错误率、解的质量、稳定性以及鲁棒性等方面均是最优的。尤其在高维时也能保持良好的性能，从而证明了该算法对于有效求解高维复杂优化问题的可行性和有效性。

然而，文中提出的GCSO算法也存在局限性，相比其他三种优化算法，参数数量有所增加，同时在D=100时对F4求解结果不是特别理想（虽然和其他三种算法相比求解结果较好，但针对F4本身而言求解结果不理想）。其实，F4函数的求解结果不理想的原因可以由“No free lunch”理论来解释。它告诉我们没有哪一种算法可以解决所有类型的优化问题。因此每种优化算法才有了不断完善与改进的空间。基于以上原因，如何进一步改善提出算法的性能，使其适合更多的测试函数，同时考虑将这种思想应用到其他实际工程问题的求解当中，这将是下一步要做的工作。

参考文献：

[1]张鹏，刘弘，刘鹏.改进的蜂群算法及其在CBD选址规划中的应用[J].计算机科学，2013（8）：210-213.

[2]魏平，徐成贤，段成德.全局智能优化集成算法研究[J].西安交通大学学报，2009，43（12）：60-64.

[3]Beheshti Z，Shamsuddin S M H.A review of populationbased meta-heuristic algorithms[J].International Journal of Advance in Soft Computing&Its Applications，2013，5（1）：1-35.

[4]高维尚，邵诚，高琴.群体智能优化中的虚拟碰撞：雨林算法[J].物理学报，2013，62（19）：28-43.

[5]Grefenstette J J.Optimization of control parameters for genetic algorithm[J].IEEE Transactions on Systems，Man and Cybernetics，1986，16（1）：122-128.

[6]Lev B，Tsoukalas J.An introduction to genetic algorithms[J].Interfaces，1999，29（3）：105-107.

[7]Fourie P C，Groenwold A A.The particle swarm optimization algorithm in size and shape optimization[J].Structural and Multidisciplinary Optimization，2002，23（4）：259-267.

[8]赵嘉，吕莉，孙辉.自适应精英反向学习的粒子群优化算法[J].小型微型计算机系统，2015，36（9）：2166-2171.

[9]Yang X S.Firefly algorithm，stochastic test functions and design optimization[J].International Journal of Bio-inspired Computation，2010，2（2）：78-84.

[10]周虎，赵辉，周欢，等.自适应精英反向学习共生生物搜索算法[J].计算机工程与应用，2016，52（19）：161-166.

[11]Walton S，Hassan O，Morgan K，et al.Modified cuckoo search：A new gradient free optimization algorithm[J].Chaos Solitons&Fractals，2011，44（9）：710-718.

[12]Rajabioun R.Cuckoo optimization algorithm[J].Applied Soft Computing，2011，11（8）：5508-5518.

[13]陈梅雯，钟一文，王李进.一种求解多维全局优化问题的改进蝙蝠算法[J].小型微型计算机系统，2015，36（12）：2749-2753.

[14]孔飞，吴定会.一种改进的鸡群算法[J].江南大学学报：自然科学版，2015，14（6）：681-688.

[15]刘天堂，江志斌，胡鸿韬，等.加强的混合遗传算法求解能力约束弧路径问题[J].上海交通大学学报，2013，47（4）：619-625.

[16]Yoshida H，Kawata K，Fukuyama Y，et al.A particle swarm optimization for reaction power and voltage control considering voltage security assessment[J].IEEE Transactions on Power Systems，2000，15（4）：1232-1239.

[17]Gandomi A H，Yang X S，Alavi A H.Mixed variable structural optimization using firefly algorithm[J].Computers&Structures，2011，89（23/24）：2325-2336.

[18]Xiao L Y，Shao W，Liang T L，et al.A combined model based on multiple seasonal patterns and modified firefly algorithm for electrical load forecasting[J].Applied Energy，2016，167：135-153.

[19]Gandomi A H，Yang X S，Ajavi A H.Cuckoo search algorithm：A metaheuristic approach to solve structural optimization problems[J].Engineering with Computers，2013，29（1）：17-35.

[20]Meng X B，Liu Y，Gao X Z，et al.A new bio-inspired algorithm：Chicken swarm optimization[C]//5th International Conference on Swarm Intelligence，2014：86-94.

[21]Das S，Suganthan P N.Differential evolution：A survey of the state-of-the-art[J].IEEE Transactions on Evolutionary Computation，2011，15（1）：4-31.