关于导数应用的教学探讨

布仁满都拉，赵迎春

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

1 引言

高等数学是很多文理专业的专业基础课，例如建筑、经济、化学、医学和物理专业等.学生的高等数学的掌握程度可能会直接影响后继其他课程的学习.高等数学的研究对象是纯数学上定义的抽象的函数，因为在实际问题中有很多变量之间的依赖关系，比如物理中速度、密度、温度和化学中的浓度一般都依赖于空间和时间，在高等数学中把这些量都抽象成函数，然后讨论它的性质及其运算.高等数学的内容比较抽象，如何提高教学效果是每位老师在想的重要问题.除互动式教学法、启发式教学法和讲练结合等我们经常采用的教学方法外，学生熟悉并吸引学生的经典例题能提高学生对知识的兴趣、学习积极性、应用能力，进而能提高课堂效果.本文中将讨论导数在物理和最优化中的有趣应用例子.

2 定义及定理

定义1[1,2]设函数f(x)的定义域为D，区间I⊂D，如果对于区间 I上任意两点 x1及 x2，当 x1＜x2时恒有f(x1)＜f(x2)，那么称函数f(x)在区间I上是单调增加的；如果对于区间I上任意两点x1及x2，当x1＜x2时恒有 f(x1)＞f(x2)，那么称函数 f(x)在区间 I上是单调减少的.

定理1[1,2]设函数f(x)在[a,b]上连续，在(a,b)内可导.

（1）如果在(a,b)内 f'(x)≥0,且等号仅在有限多个点处成立，那么函数f(x)在[a,b]上单调增加；

（2）如果在(a,b)内 f'(x)≤0,且等号仅在有限多个点处成立，那么函数f(x)在[a,b]上单调减少.

定义2[1,2]设f(x)在区间I上连续，如果对I上任意两点 x1及 x2恒有 f[(x1+x2)/2]＜[f(x1)+f(x2)]/2，那么称f(x)在区间I上的图形是凹的；如果恒有f[(x1+x2)/2]＞[f(x1)+f(x2)]/2，那么称f(x) 在区间I上的图形是凸的.

定理2[1,2]设函数f(x)在[a,b]上连续，在(a,b)内具有一阶和二阶导数，那么

（1）若在(a,b)内 f"(x)＞0，则函数 f(x)在[a,b]上的图是凹的；

（2）若在(a,b)内 f"(x)＜0，则函数 f(x)在[a,b]上的图是凸的.

拉格朗日中值定理3[1,2]如果函数f(x)满足

（1）在闭区间[a,b]上连续；

（2）在开区间(a,b)内可导，

那么在(a,b)内至少有一点ξ，使等式

成立.

定义3[1,2]设函数f(x)在点x0的某邻域U(x0)内有定义，如果对于对应的去心邻域Uo(x0)内的任一x，有 f(x)＜f(x0)(或 f(x)＞f(x0))那么就称 f(x0)是函数 f(x)的一个极大值（或极小值）.

定理4[1,2]设函数f(x)在点x0处连续，且在x0的某去心邻域Uo(x0,δ)内可导.若 x∈(x0-δ,x0)时，f'(x)＞0(或 f'(x)＜0)，而 x∈(x0,x0+δ)时，f'(x)＜0(或 f'(x)＞0)，则f(x)在x0处取得极大值(或极小值).

3 例子

我们可以用定理1和2求函数的单调区间和凹凸区间，反过来也可以利用定理1和2，根据函数图形判断一阶和二阶导数的符号[3]，如下例：

例1 设某质点沿直线运动.质点于时刻t在直线上的位置为x，即位置函数为x=f(t).在图1中给出x=f(t)的图形.下面我们利用定理1和2，从图1判断质点的运动状态(图2).

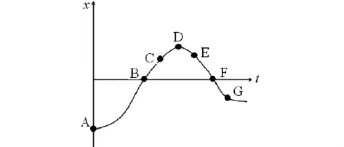
图1 位置x随时间t的变化

图2 质点的速度和加速度

由图1看出，在区间(0,tB)上位置函数x=f(t)单调递增并且是凸的，所以位置函数x=f(t)的一阶和二阶导数即速度和加速度都大于零，因此，时刻tA处的速度和加速度都大于零（见图2A）,即质点沿x轴的正方向加速运动.在时刻tB，凹凸改变，二阶导数等于零，速度达到最大值.在时间段（tB,tF）上图形是凸，所以二阶导数小于零，即加速度是负的，质点开始做减速运动，例如在时刻tc，速度是正的，加速度是负的.到时刻tD时，速度减少为零.过时刻tD后，速度变为负的，即开始反方向即x轴的负方向运动，因为加速度也是负的，所以质点沿x轴的负方向加速运动，例如在时刻tE，速度和加速都是负的.在时刻tF，凹凸性改变，加速度为零，速度达到最大值.过时刻tF后（例如tG时刻），加速度变为正.因为速度和加速度的符号相反，所以质点做减速运动.

例2 如果一个汽车从零加速在8秒内走了107.2896米，它在这8秒内的平均速度为13.4112米/秒.由拉格朗日中值定理知在这个加速运动过程中，一些点上瞬时速度等于平均速度13.4112米/秒.

例3 介质中光的速度依赖于介质，一般介质密度越高，光传播速度越慢.根据光学中的费马原理，光沿所用传播时间最短的路径，从一点传播到另一个点.假设光线从介质1的点A到介质2点B，介质1和2中光速分别等于c1和c2，描述该路径.

解 因为光沿最快的路线从点A传播到点B，所以我们寻找一个路径使传播时间最短.这问题是求极值和最小值的问题.建立如图3的直角坐标系.θ1和θ2分别为入射角和折射角.

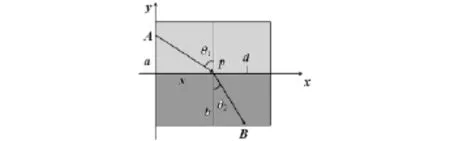
图3 光的折射

光从A到P的所需时间（记为t1）等于t1=AP/c1；光从P到B的所需时间（记为t2）等于t2=PB/c2，所以光从A到B的所需时间（记为t）等于

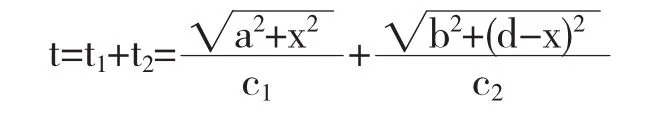
上式表明t是x∈[0,d]的可微函数.

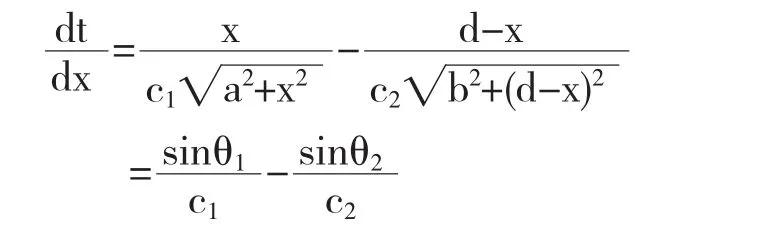
可以证明在[0,d]上的连续单调增加函数，并且，根据介值定理和单调性可知存在唯一由定理4可知函数t=t(x)在x0处取得最小值.在x0处（即点P），我们可得最佳路径的入射角，折射角，介质1和2内光速之间的关系

很多学生都有这样疑问：高等数学的这些抽象的内容实际当中如何用呢？我们通过学生容易理解的实际例子（如例1,2，3）的讲解，告诉学生很多实际问题一般先建立数学模型，然后求该数学模型的解，在整个这个过程当中都会用到高等数学的内容.这样我们能提高学生对高等数学认识、学习兴趣和应用能力.并这样做能加深理论知识的掌握.这些经典例子能提高课堂教学效果.

〔1〕 同济大学数学系.高等数学[M].高等教育出版社，2014.

〔2〕 GB Thomas,MD Weir,J Hass.Thomas'calculus[M].Pearson Education,Inc.2010.

〔3〕 HD.Young,RA.Freedman,AL.Ford.University physics with modern physics[M].Pearson Education,Inc.2011.