一种新的基于时空混沌的伪随机数发生器

王 永，马键滨，陈 燕，何 波

WANG Yong1，2,MAJianbin1,CHEN Yan1,HE Bo2

1.重庆邮电大学 计算机科学与技术学院，重庆 400065

2.重庆邮电大学 电子商务与现代物流重点实验室，重庆 400065

1.College of Computer Science and Technology,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

2.Key Laboratory of Electronic Commerce and Logistics,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

1 引言

流密码技术被广泛用于数据传输、信息加密等领域，其核心是设计安全高效的伪随机数发生器[1-2]。伴随着混沌密码的发展，时空混沌系统以其在空间和时间上具有复杂的动力学行为的优点被应用于加密领域。

最近，一些基于混沌系统的伪随机数发生器算法被提出[3-5]。这些算法分别是基于组合混沌映射、分段非线性映射和高维混沌映射，其设计思想均是利用混沌的伪随机性来构建加密方案。为进一步增强混沌系统的性能，一些研究者提出了基于耦合映像格子模型的混沌加密方案[6-8]。然而，这些方案中均存在混沌模型概率密度分布不均匀的问题。针对上述问题，本文将分段Logistic映射[9]作为改进时空混沌模型的局部映射，通过变耦合系数的方法，提升混沌系统自身的密码学特性，从而提升算法的性能。仿真实验表明本文提出的伪随机数产生算法具有良好统计性和效率高的特点，具有很好的应用潜力。

2 Logistic混沌映射及分段形式

2.1 Logistic混沌映射

Logistic混沌映射由于其表达式简单，随机性能良好，常被用于混沌保密通信的各个领域，其数学表达公式如下：

其中x0∈(-1,1)，μ∈(1.4,2]时，系统进入混沌状态。

2.2 分段Logistic映射

分段Logistic映射有两种分段形式[10]，根据文献[9-11]中的研究，可知分段Logistic映射具有优于Logistic映射的密码学性能。因此，为提升Logistic映射的性能，本文提出如下分段Logistic映射，其表达式如下：

2.3 局部混沌映射的特性分析

本文拟通过对局部混沌映射性能的提升，从而提升整个时空混沌系统的性能，为设计伪随机数发生器奠定良好的基础。

2.3.1 分岔图

Logistic映射和分段Logistic映射(N=64)的分岔图如图1所示。从图中可以明显看出分段Logistic映射的倍周期分岔速度比Logistic映射更快。系统处于混沌状态时所对应的参数μ的取值范围更大，更适合用于密码算法设计。

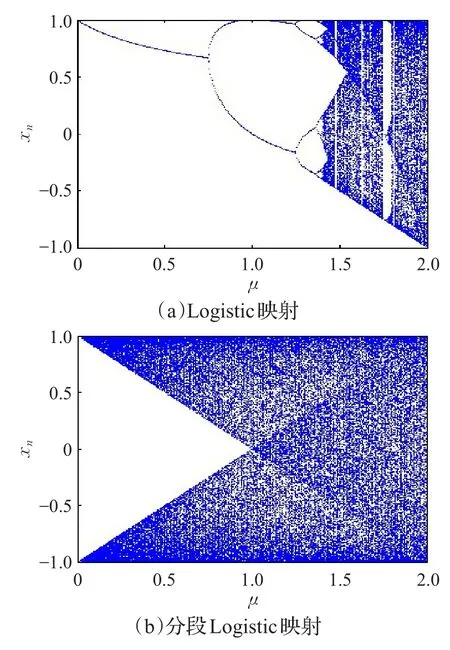
图1 局部映射的分岔图

2.3.2 Lyapunov指数

Lyapunov指数用于量度相空间中相近轨道的平均收敛性或平均发散性。最大Lyapunov指数（LLE）是描述系统混沌程度的一个重要指标。对于函数xn+1=f(xn)的Lyapunov指数λ表示如下：

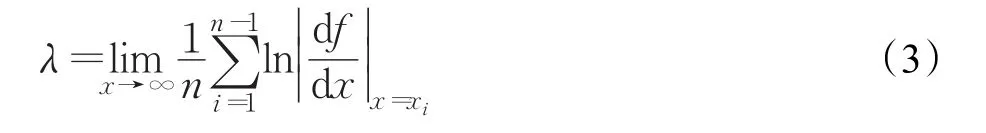
根据公式（3）计算Logistic映射和分段Logistic映射(N=64)的Lyapunov指数，Lyapunov指数随参数μ的变化情况如图2所示。从图中可以看出，分段Logistic映射的Lyapunov指数值大于Logistic映射的Lyapunov指数值。此外，Logistic映射当系统参数取μ∈（1.4，2]时具有稳定的混沌状态，分段Logistic映射当系统参数取μ∈（0，2]时具有稳定的混沌状态。因此，分段Logistic映射运动轨迹更加不稳定，系统混乱程度更高，对该映射产生序列的分析预测更加困难，安全性得到提高。

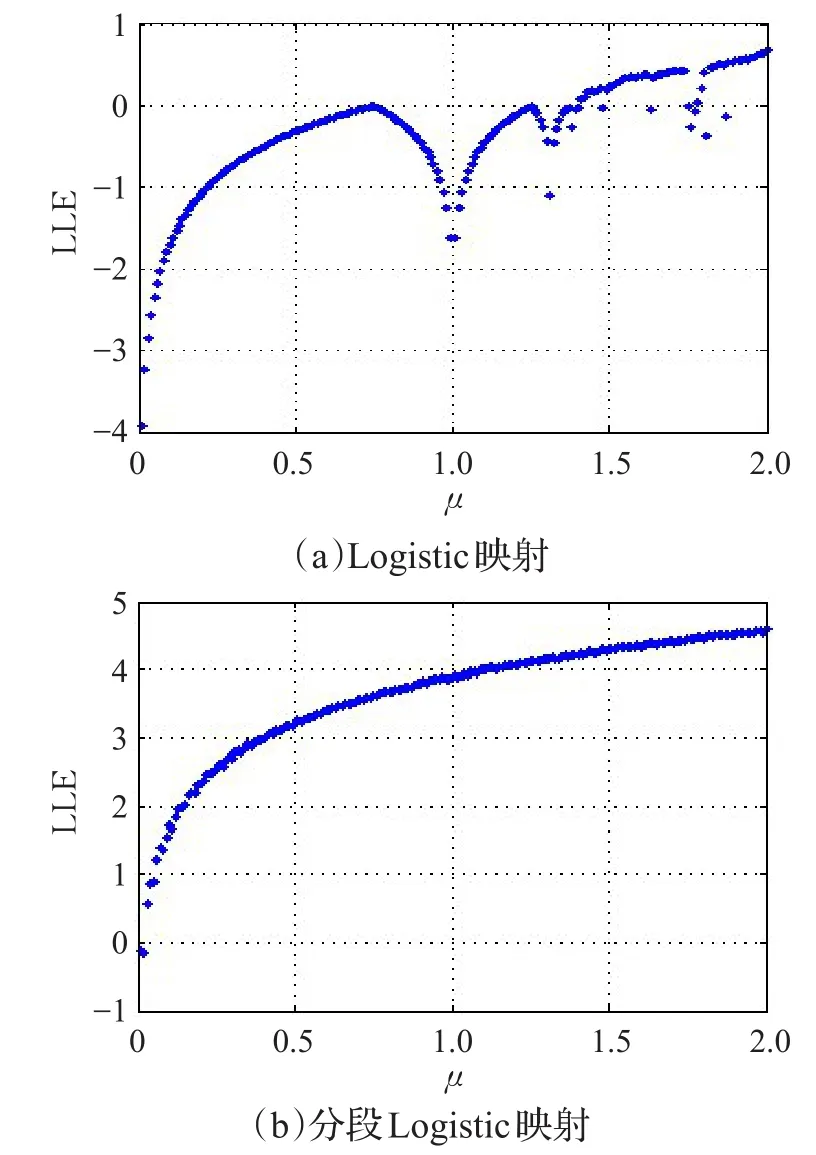
图2 局部映射的Lyapunov指数

3 时空混沌

3.1 时空混沌模型

本文选用时空混沌中临近二维耦合映像格子模型（Nearest-neighboring Coupled Map Lattices，NCML）作为设计伪随机数发生器的核心部件，其表达式为：

其中，n=1,2,3,…,为时间索引；i=1,2,…,R为模型格子的行坐标；j=1,2,…,L为格子的列坐标；f(x)为局部混沌映射，ε∈(0,1)为耦合系数。同时，设置式（4）的周期边界条件为。此处，式（2）所示的分段Logistic映射作为该模型的局部映射，并根据文献[9]中的研究结果，将N设置为64。

3.2 模型特性分析

根据2.3节中对比分析局部映射之间的特性差异，进而分析时空混沌模型之间性能的变化。

3.2.1 时空混沌的Lyapunov指数

时空混沌模型中，设置参数R=L=8。分别计算局部映射为Logistic映射和分段Logistic映射的时空混沌的最大Lyapunov指数随参数μ的变化情况如图3所示。可以看出，局部映射为分段Logistic映射的时空混沌系统的混沌特性得到了有效的提升。

图3 时空混沌模型的最大Lyapunov指数

3.2.2 概率密度分布

一个良好的伪随机数发生器满足概率密度均匀分布。混沌映射的概率密度分布能反映混沌映射的优劣，决定伪随机数发生器算法的性能。为此，进行如下测试，将区间[-1，1]等分为1 000区间，然后迭代混沌映射若干次，统计每个区间内状态值出现的概率。不同混沌映射的概率密度分布情况如图4所示，从图中可以看出，分段Logistic映射的概率密度相较于Logistic映射均不均匀。局部映射为分段Logistic映射和Logistic映射的时空混沌，概率密度分布在均匀性上有一定的改进，但仍然是不均匀的。

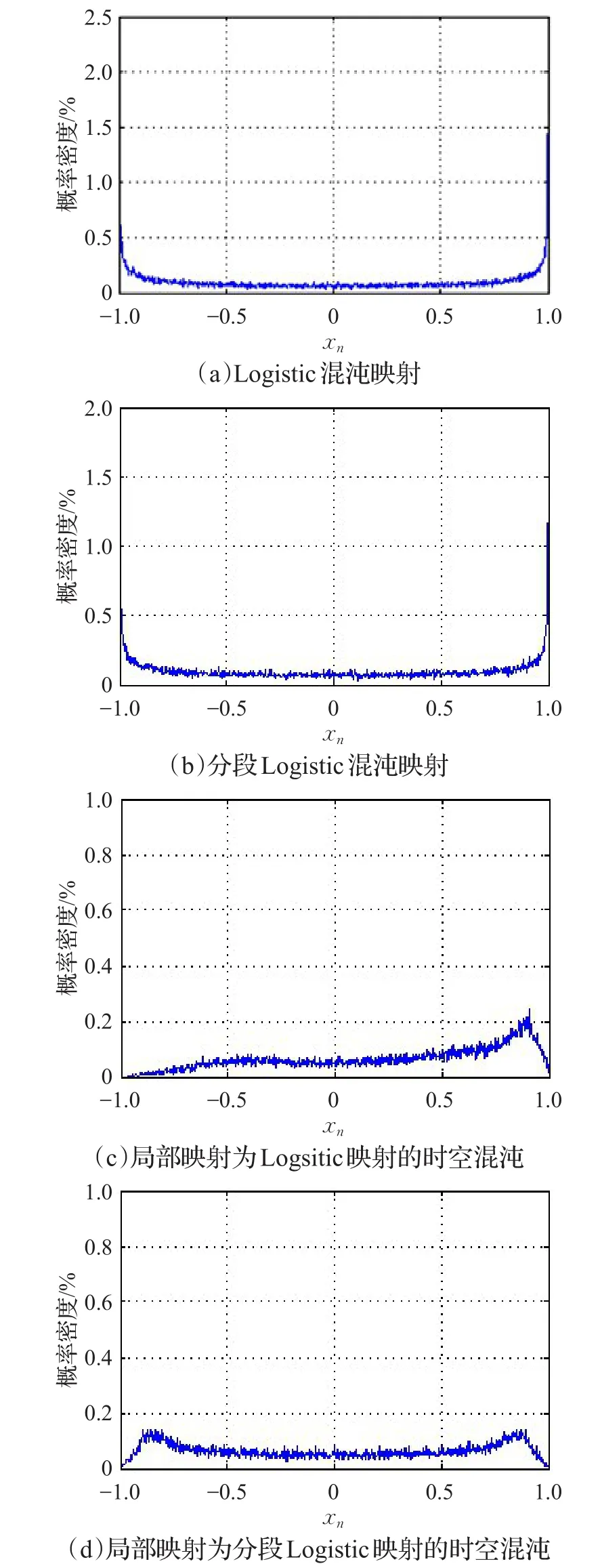
图4 混沌映射的概率密度分布情况

4 伪随机数发生器

4.1 变耦合强度的时空混沌模型

为解决3.2.2节中时空混沌模型概率密度分布不均匀的缺陷，提出改变时空混沌耦合系数的策略，即设置耦合参数的下限值为εmin=0.005，上限值εmax=0.7。然后，调整耦合系数从εmin到εmax变化，即每迭代一次时空混沌系统，ε变化一次，具体过程如图5伪代码所示。

图5 ε变化的伪代码

采用策略后，重新测试局部映射为分段Logistic映射的时空混沌模型的密度概率分布情况，由图6可以看出模型概率密度的均匀分布性得到了显著提高。

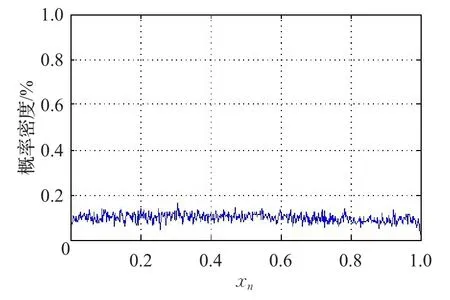
图6 变耦合强度的NCML生成序列的分布情况

4.2 伪随机数发生器方案

该方案详细步骤如下：

步骤1迭代分段Logistic映射产生初始序列{xi}，其中 {xi}={x0,x1,…,xR×L-1}。

步骤2将初始序列{xi}放入时空混沌中，进行NCML迭代一次，得到变化后的{xi}={x0,x1,…,xR×L-1}序列，然后将{xi}中的每一个状态值抽取8个比特（小数点后的9至16位）转化为0～255值的序列{Xi}={X0,X1,…,XR×L-1}。

步骤3根据高级加密标准（Advanced Encryption Standard，AES）S盒对步骤2中产生的序列进行替换操作，替换操作后的序列{Yi}为NCML当前轮次下输出的伪随机数。其中替换规则如下：

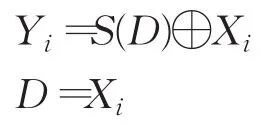
其中，i=0,1,…,R×L-1；寄存器初值 D取[0，255]内的任意值，然后根据Xi更新寄存器D的值；因此最终得到的伪随机序列是{Yi}={Y0,Y1,…,YR×L-1}。

步骤4每循环一次后，根据4.1节中提到方法调整时空混沌的耦合系数ε。

重复步骤1～3，得到任意长度的伪随机序列。

5 算法安全测试与分析

5.1 密钥空间分析

一个安全的加密系统应该具备足够大的密钥空间，一般说来，密钥空间应大于2128。本文算法的密钥由改进的时空混沌的四个初始参数组成，分别为：初始值x0，局部映射的参数μ，耦合系数ε，寄存器初值D，其中 x0∈(-1,1),μ∈(0,2],ε∈(0,1),D∈[0,255]，假设浮点数精度为10-14，则x0的取值为2×1014可能值中的任意一个。类似地μ的取值为2×1014可能值中的任意一个，ε的取值为1014可能值中的任意一个，D的取值为255范围内的任何整数值。因此，整个密钥空间的大小约为1×1045，则密钥空间为1×1045＞2128，满足暴力破解要求。

5.2 密钥敏感性分析

密钥敏感性，即密钥很小的一点变化，会导致密文发生很大的变化。下面对密钥敏感性进行如下的测试。

首先改动如下：

Case1密钥初始值 x0由0.123 456 789更改为x0+Δx；

Case2将μ由2更改为μ-Δμ；

Case3将 ε0由0.05更改为 ε0+Δε；

Case4将D由3更改为4。

其中，Δx=10-14,Δμ=10-14,Δε=10-14。然后比较改变前后生成序列之间的差别。量化差别，测试序列之间的相关性。分别在四种情况下循环100次时空混沌得到一个6 400伪随机数的序列，与原序列进行测试，得到的结果如表1所示。

表1 原序列和4个序列之间的相关系数

从表1可以看出所有的相关系数非常小，这意味着没有检测到原序列和4个序列之间存在相关性。因此，该方案具有很高的密钥敏感性。

5.3 伪随机序列的测试与随机性对比分析

美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）提供了15个检测指标[12]，鉴别一个随机或伪随机序列是否为随机序列。将伪随机序列中的数转换为二进制序列进行测试，每项测试指标归一化后的检测结果被称之为P_value值。预先设置阈值α，若P_value值大于阈值α，则表明方案产生序列的随机性具有1-α的可信度。设置α为0.01，这表明若序列通过测试，则其随机性具有99%的可信度。因此，通过本文方案得到2 000条长度为1 000 000比特的序列，测试每个序列的15个检测指标，均通过了检测，各指标的P_value值如表2所示。测试本文与文献[13-14]算法产生的随机数序列的15项指标的P_value值如表3所示。从表中对比可知，各项指标的值非常接近，并且本文算法产生的随机序列测试的FBT、BMRT等值大于上述文献算法中的值。另一方面，统计不同算法产生的100条随机序列，进而比较序列的通过率，本文算法产生序列的各项指标通过率为99.29%，略高于文献[13]的98.82%，表明本文算法产生的伪随机序列有更好的随机性。

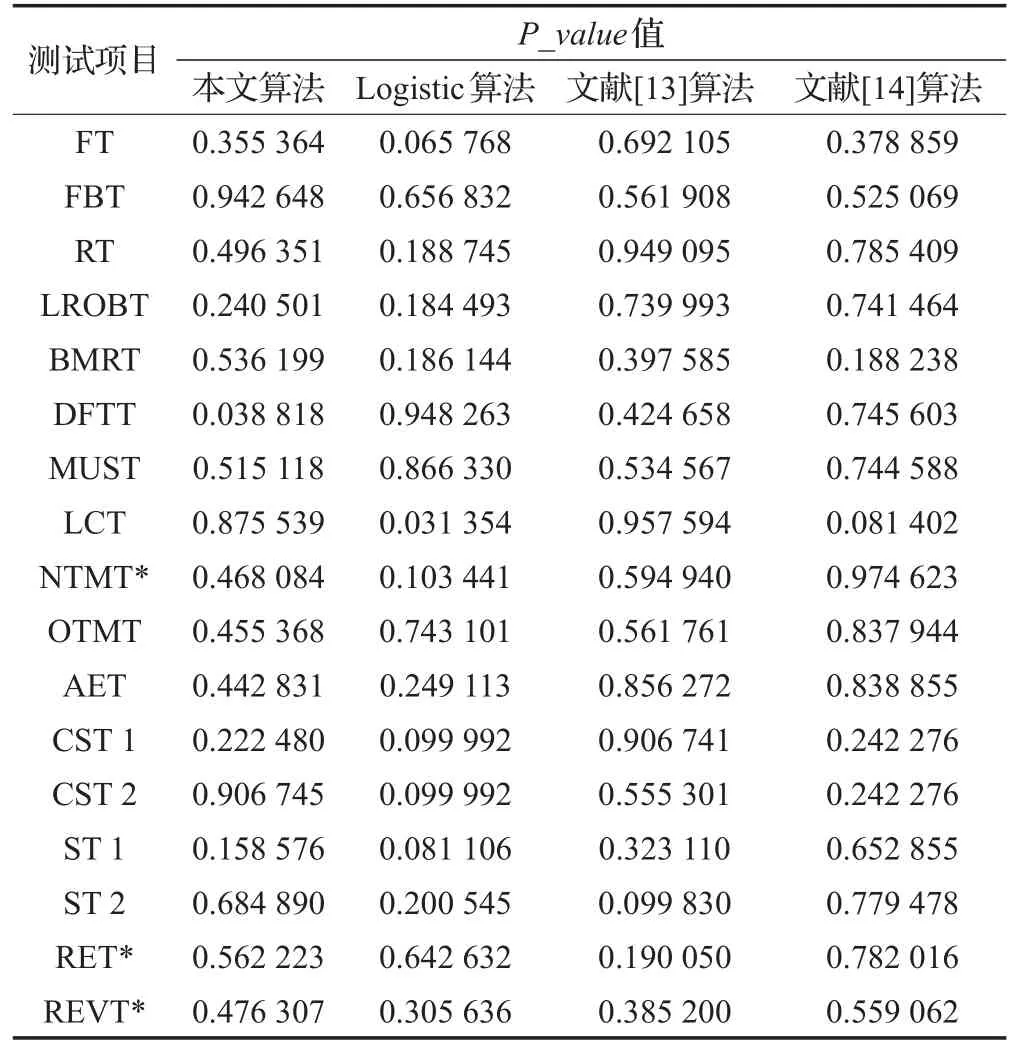
表3 算法结果对比

5.4 速度对比分析

本算法中，迭代一次时空混沌系统可以产生64个字节的伪随机数，对每一个伪随机数取小数点后8比特位，即512比特伪随机序列段。而如果用混沌密码典型的迭代和取整操作，产生64字节的伪随机数则需要迭代时空混沌映射系统16次。最近，一些基于混沌映射的伪随机数生成器方案[9，15-16]被提出。其中，文献[15]是基于Logistic映射的；文献[16]中的三种算法是基于时空混沌系统的。为了验证不同方案产生伪随机数序列的效率，分别在一台配置为3.30 GHz Intel Core i5-4590 CPU，8 GB RAM电脑，操作系统为Win 7，在Visual C++6.0平台下实现本文和文献中的算法。算法的运行速度统计结果如表4所示，从表中可以看出本文提出的方案在效率上得到了极大的提高。

表4 产生伪随机序列算法的运行速度

6 结束语

在本文方案中，为获得更好的复杂性，对时空混沌模型进行分析，为得到良好的混沌特性，将时空混沌的局部映射进行了改进，即分段Logistic映射。分别测试改进后混沌映射的相关特性，结果表明本文方案在Lyapunov指数、概率密度分布等方面都有很好的改进，从而产生的伪随机序列安全性和效率得到提高。实验表明本文的加密方案能产生良好性能的伪随机序列。

参考文献：

[1]Wang X Y，Yu Q.A block encryption algorithm based on dynamic sequences of multiple chaotic systems[J].Communications in Nonlinear Science&Numerical Simulation，2009，14（2）：574-581.

[2]Li X，Li C，Lee I K.Chaotic image encryption using pseudorandom masks and pixel mapping[J].Signal Processing，2016，125（C）：48-63.

[3]Wang X Y，Yang L.Design of pseudo-random bit generator based on chaotic maps[J].International Journal of Modern Physics B，2012，26（32）.

[4]Wang X Y，Wang X J.Design of chaotic pseudo-random bit generator and its applications in stream-cipher cryptography[J].International Journal of Modern Physics C，2008，19（5）：813-820.

[5]Wang Y，Wong K W，Liao X F，et al.A new chaosbased fast image encryption algorithm[J].Applied Soft Computing，2011，11（1）：514-522.

[6]Zhang Y Q，Wang X Y.A new image encryption algorithm based on non-adjacent coupled map lattices[J].Applied Soft Computing，2015，26：10-20.

[7]Teng L，Wang X Y.A bit-level image encryption algorithm based on spatiotemporal chaotic system and selfadaptive[J].Opt Commun，2012，285：4048-4054.

[8]Zhang Y Q，Wang X Y.A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice[J].Information Sciences，2014，273：329-351.

[9]Wang Y，Liu Z，Ma J，et al.A pseudorandom number generator based on piecewise logistic map[J].Nonlinear Dynamics，2015，83（4）：2373-2391.

[10]范九伦，张雪锋.分段Logistic混沌映射及其性能分析[J].电子学报，2009，37（4）：720-725.

[11]张雪锋，范九伦.一种新的分段非线性混沌映射及其性能分析[J].物理学报，2010，59（4）：2298-2304.

[12]Rukhin A，Soto J，Nechvatal J，et al.NIST Special Publication 800-22：A statistical test suite for the validation of random number generators and pseudo random number generators for cryptographic applications[S].rev1a，2010.

[13]Wang X Y，Xie Y X.A design of pseudo-random bit generator based on single chaotic system[J].International Journal of Modern Physics C，2012，23（3）.

[14]Wang Xingyuan，Qin Xue，Xie Yixin.Pseudo-random sequences generated by a class of one-dimensional smooth map[J].Chinese Physics Letters，2011，28（8）.

[15]Pareek N K，Patidar V，Sud K K.A pseudo random bit generator based on chaotic logistic map and its statistical testing[J].Informatica，2009，33：441-552.

[16]Li P，Li Z，Halang W A，et al.A multiple pseudorandombit generator based on a spatiotemporal[J].Physics Letters A，2006，349：467-573.