基于滑模双环控制的感应耦合电能传输系统设计
龚 明, 李 强
(1. 北京交通大学机械与电子控制工程学院, 北京 100044; 2. 中车工业研究院有限公司, 北京 100070)
传统的电能传输主要是利用金属导线的直接接触来进行的,这种直接连接的电能传输方式被广泛运用,但这样传统的供电方式存在一些不足之处:磨损问题、接触电火花、导线的裸露而产生的不安全因素及不美观等[1].而且现在生活中的电子类产品越来越多,导线和插座充电的方式逐渐不能适应社会的发展,感应耦合电能传输技术应运而生,作为新兴的电能传输技术带给了人们希望,与传统的供电方式相比,感应耦合电能传输技术通过发射端与拾取端之间非接触的方式实现电能传输,可以解决传统供电方式的不足.特别是针对轨道交通,可以解决传统牵引网和第三轨供电方式中由于移动磨损、供电体裸露等产生的问题,还可为化工设备中的检测装置、水下机器人、分布式传感器等的供电提供可靠的电能供应,具有绿色环保、少维护等优点[2].
感应耦合电能传输系统运用于轨道交通等的无线充电,在负载频繁波动、参数变化的情况下保证系统输出电压的稳定非常重要.逆变器作为感应耦合电能传输系统中重要的组成部分,其非线性特性使得系统输出控制难度较大,在负载波动频繁或参数变化的情况下,传统控制方式需要较长的恢复时间,难以满足轨道交通供电要求.
针对感应耦合电能传输系统,对系统整体进行双环控制研究的文献很少,大多只是对逆变器进行双环控制的研究,而且采用的多为传统的控制方式,文献[3-4]中提出了基于比例-积分-微分(proportion integration differentiation, PID)调节器的双环控制,而且归纳了双环控制的优点,但是对于逆变器的非线性特性,在负载波动或者参数变化下,传统的PID控制方式的控制效果和控制速度不能够满足轨道交通供电的要求.传统双闭环控制策略的PI调节器控制参数为常数且较为敏感,在系统启动和负载变动时,存在动态响应速度慢、抗干扰性能差等问题[5].本文把滑模控制作为内环的控制,因为滑模控制对系统模型精度要求不高,对参数变化和外部扰动不敏感[5],所以避免了控制参数的敏感性,使得该双环控制系统具有更强的抗干扰性,更快的响应速度,本文对系统采用的双环控制策略是以滑模控制对原边电流的控制作为内环,以PI控制对系统输出电压的控制作为外环,利用外环电压误差控制信号和输出滤波电感电流状态反馈方案得到控制电流,通过内环滑模控制来调节原边电流,使系统输出电压跟踪参考值.单环控制的动态调节速度比较慢,在外界扰动时很难获得理想的动态响应,双环控制比单环控制的性能优越,电流内环扩大逆变器控制系统的带宽,使得逆变器动态响应加快,非线性负载适应能力加强,输出电压的谐波含量减小,控制也比较方便,电压外环电流内环的双环控制方案也是高性能逆变电源的发展方向之一[6].
1 系统建模
感应耦合电能传输系统的原副边间有大的空气间隙,是松耦合,为补偿大的漏感,通常在原副边增加电容,串-串、串-并的补偿方式被广泛地使用,如图1所示,本文选择的是串-并结构,系统主要由高频逆变、原边补偿、原副线圈、副边补偿、整流、滤波网络组成,在原边,S1~S44个转换开关组成了全桥逆变器,副边是整流二极管D1~D4,逆变器转换开关和整流二极管通过2个谐振回路被分开,2个谐振回路是由补偿电容(C1和C2)和原副线圈(L11和L22)组成.直流电流经过逆变后变换成高频的交变电流(i1),并输入到原边线圈绕组中,在高频的电磁场感应耦合的作用下将电能传输到副边,副边得到的高频交变电流(i2)经不可控全桥整流,其输出经滤波网络滤波为负载供电[7].

图1 感应耦合电能传输系统电路Fig.1 Inductively coupled power transfer system circuit
1.1 系统原边建模
系统原边的等效电路如图2所示,图中副边系统等效到原边的等效阻抗为[8]
(1)
式中:M为原、副边线圈的互感,
ω0=(L22C2)-0.5.

图2 系统原边的等效电路Fig.2 Equivalent circuit of the primary side of the system
图2中:vs为逆变器的输出电压;vC为电容电压;Req为等效电阻,包括原边线圈内阻和副边系统等效到原边的电阻;Leq为等效电感.
对于单相全桥逆变器的串联谐振电路,一些文献采用的是利用状态空间平均法得到连续的数学模型[9],一些是建立理想简化的统一离散模型[10].本文为使模型简化、有效,建立离散时间动态模型,t=0时,逆变器的输出电压为vs,t>0时,i1和vC的时域方程表达式为
(2)
vC(t)=vs+e-αt(vC(0)-
(3)
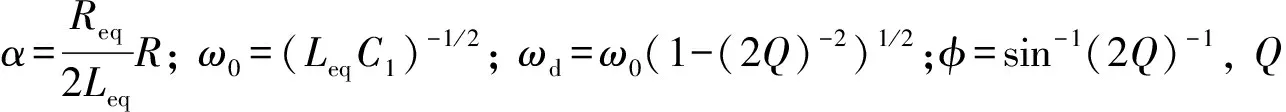
逆变器的输出电压是由逆变器的开关状态决定的,t>0时,
vs(t)=VDCM(k)signi0(t),
kT (4) 式中:k=1,2,…;VDC为逆变器的直流输入电压;T=π/ωd为半个振荡周期;M(k)为逆变器功率运行状态,M=1时,电路工作在输入功率模式,使输出电流持续的增加,M=0时,电路为自由衰减的模式,在负载消耗的作用下使输出电流减小. 假设Q≫1,由式(2)和式(3)得离散时间方程为 (5) VC(k+1)=|vC(kT+T)|, (6) 式中:I0为时间T内输出电流i1的峰值绝对值;VC为开关瞬间的电容电压. 把式(6)代入式(5),可得离散电流状态方程: I0(k+1)=AI0(k)+Bu(k+1), (7) 式中: A=e-π/(2Q)≈1-π(2Q)-1; u(k+1)=(M(k)+M(k+1))/2; B=2VDC(ReqQ)-1e-π/(4Q)≈ 2VDC(ReqQ)-1(1-π(4Q)-1). 图3是副边系统的等效电路图,图中:v12为原边线圈在副边产生的感应电压;r22为副边线圈内阻;vL为整流输出电压;iR为负载电流;v0为输出电压. 对于副边系统,本文采用大信号建模的方法,大信号模型是把所有的状态变量转换成缓慢变化的直流量,便于控制[11].如图3,既有整流器输入侧的交流部分(AC),又有输出滤波的直流部分(DC),因此需分别进行建模,为使两种信号结合为一个模型,通过多频建模(multiple frequency modeling, MFM)技术[12-13]把交流量转换成d-q量(缓慢变化的直流值),利用广义状态空间建模技术对交流、直流侧建模,再采用线性化方案线性化整流器带来的非线性,就可得到一个集合的线性化大信号模型,便于内环参考电流的计算,简化降阶传输函数,方便外环PI控制器的设计. 图3 副边系统的等效电路Fig.3 Equivalent circuit of the secondary side of the system 1.2.1交流子系统的建模 图4是交流子系统等效电路图,电压电流的关系可描述为 (8) (9) 图4 AC子系统的等效电路Fig.4 Equivalent circuit of AC subsystem 将交流状态量iL、v2、i2、v12通过MFM技术转换成等效的直流量,可用傅里叶级数表达[14-15],若系统的基频为ω0,则状态变量可被描述为 iL(t)=iLd(t)sinω0t+iLq(t)cosω0t, (10) v12(t)=v12d(t)sinω0t+v12q(t)cosω0t, (11) v2(t)=v2d(t)sinω0t+v2q(t)cosω0t, (12) i2(t)=i2d(t)sinω0t+i2q(t)cosω0t, (13) 式(10)~(13)中:iLd、iLq为采用MFM多频建模时iL在d、q轴d的分量;类似地,v12d、v12q、v2d、v2q、i2d、i2q分别为v12、v2、i2在d、q轴的分量. 把式(10)~(13)代入式(8)和式(9),使sin和cos的系数相等,可得 v12d(t)=v2d(t)+r22iLd(t)+ (14) v12q(t)=v2q(t)+r22iLq(t)+ (15) (16) (17) 用状态空间方程表示为 (18) 式中: x1(t)=[iLdiLqv2dv2q]T; u1(t)=[v12dv12qi2di2q]T; 1.2.2直流子系统建模 图5 直流子系统的等效电路Fig.5 Equivalent circuit of the DC subsystem 电压电流的关系为 (19) (20) 用状态空间方程表示为 (21) 1.2.3线性化大信号模型 由式(10)~(13)可知, (22) 由于交流侧输出功率等于直流侧的输入功率,所以 (23) 由式(22)和式(23)可得 (24) (25) 式(22)和式(25)描述了整流器的非线性特性. 当交流系统处于稳态时,由式(18)可得 0=A1x1(t)+B1u1(t), (26) 用稳态量表示为 (27) 根据式(27),得到V12d、V12q、I2d和I2q之间稳态量的关系为 r22I2d+(-ω0L22)I2q, (28) ω0L22I2d+r22I2q. (29) 从整流器的输入看,可以等效为一个电阻[18],所以若令V2q=0,那么I2q=0.结合式(22)和式(25)得 (30) i2d=(4/π)iL0. (31) (32) 当V12满足式(32)时可以使式(22)的平方根关系转换成简单增益,实现线性化.V2d是和输出电压成比例的,所以交流系统可被描述为式(33),其中,vc是对输出电压v0的控制输入. (33) 结合式(31)和式(33)可得 (34) 由式(18)、(21)、(34),得到集合线性化大信号模型的状态方程为 (35) 式中: x(t)=[iLdiLqv2dv2qiL0v0]T; y(t)=v0; u(t)=[vci0]T; C=[0 0 0 0 0 1]; 线性化方案是以输出滤波的电感电流iL0为状态反馈量,用公式明确地表示出需要的输入电压(V12d和V12q),在谐振回路的输出(V2d和V2q)其中任何一个为0时,使整流器带来的平方根变成简单的增益,使其级联成一个集合的线性化大信号模型[11]. 本文采用的双环控制策略是以滑模控制对原边电流的控制作为内环,以PI控制对系统输出电压的控制作为外环,系统框图如图6所示,图中模块1是式(34)和式(36),模块2是指感应耦合电能传输系统.在外环控制中,Vref为参考输入电压,控制信号是采样滤波电感电流iL0和输出电压v0,用外环电压误差的PI控制输出信号和状态反馈iL0,根据式(34)得到副边需要的输入电压的幅值绝对值,通过式(36)得到原边所需要的参考电流的幅值绝对值Iref;内环控制是采样原边电流幅值绝对值和Iref比较得到电流误差,通过滑模控制得到导通角δ,驱动逆变器开关来调节原边电流,从而调节副边的输入电压,达到控制系统输出电压v0的目的. v12=ωMIref. (36) 图6 双环控制系统框图Fig.6 Double-loop control system block diagram 对于电流内环控制,选择的是滑模控制策略,滑模控制的研究对于能满足要求的智能控制方法在逆变器的运用是最为广泛的.它是一种非线性控制,在预先设计的滑模面上快速地切换系统的控制状态,具有高频开关特性,特别适用于电力电子装置的开关控制,对系统模型精度要求不高,对参数变化和外部扰动不敏感,具有动态响应速度快、抗干扰能力强、控制规律简单和实现容易等优点[5]. 线性滑模面在遇到扰动时稳态误差较大,所以在线性切换函数的基础上加入了积分项,采用电流误差积分滑模面[16],切换函数设计为 S(k)=Ie(k)+kif(k), (37) f(k+1)=f(k)+TIe(k), (38) 式中:S为滑模切换面; ki为积分增益; Ie为电流误差,其中Ie=Iref-I0. 针对不确定和外加干扰的系统,一般采用的控制律为等效控制加切换控制,切换控制可以实现对不确定性和外加干扰的鲁棒控制,将保证系统状态轨迹到达并收敛到滑模面的邻近区域.本文采用基于等效控制的函数切换控制律. (1) 等效控制 离散系统进入理想滑动模态时, S(k+1)=S(k), (39) 由电流的离散状态方程式(7),结合式(37)和式(39)可得等效控制方法得到的控制量 ueq(k+1)=(1-A)/BI0(k)+kiT/BIe(k). (40) (2) 切换控制 由切换控制方法得到的控制量 ud(k)=u0sgnS(k). (41) 基于等效控制的函数切换控制律可表示为 u(k)=ueq(k)+u0sgnS(k), (42) 式中:u(k)为逆变器开关的导通角. 2.1.1参数范围分析 由式(37)可知,系统的响应速度完全和ki有关,ki设计恰当就能有效消除基频的偏移量,获得稳定电流.ki的大小必须使滑动模态的到达条件得到满足: S(k)[S(k+1)-S(k)]<0, (43) 即可得到最大增益值[17]: (44) 式中:Imax=B/(1-A)=4VDC/(πReq) 当Iref=0、Iref=Imax时为电流控制极限值,得到增益范围为 0 (45) 2.1.2存在性和可达性分析 定义李雅普诺夫函数 (46) 其增量ΔV(k)只要满足条件式(47),S(k)=0就是全局渐近稳定的平衡面[18]. S(k)≠0. (47) 由式(7)、式(37)、式(38)、式(40)和式(42)可得 S(k+1)-S(k)=(1-A)I0(k)-Bu(k+1)+ kiTIe(k)=-Bu0sgnS(k) , (48) 其中,根据式(7)可知B>0,则根据式(48)得 sgnS(k)[S(k+1)-S(k)]<0. (49) 假设采样周期T很小时,可知 sgnS(k)[S(k+1)+S(k)]>0, (50) (51) 满足李雅普诺夫稳定性定理. 为了能准确地反馈电流内环所需要调节的电流Iref,电压外环选择PI控制.由式(35)可得系统的输出电压和整流器的控制输入电压之间的传递函数为 (52) Bij是B的第i行第j列,该模型是6阶的,不利于PI控制器的设计和参数整定.通过比较式(32)和式(33)可知,在稳态时,V2d=Vc,Vc为vc的稳态值,所以由式(30)和式(52)可知G1(s)可近似为 (53) 通过状态空间方程(21)推导可知, (54) 可用简化的二阶传递函数(54)进行PI控制器设计[11]. 通过两个传递函数的伯德图和阶跃响应进行对比,如图7所示. (a) Bode图 (b) 阶跃响应图7 近似和实际传函比较Fig.7 Approximation compared to the actual transfer function 从图7中证明,在低频时近似传函和实际传函的性能是相似的,高频的动态性能通过输出滤波被衰减,所以可以用于简化的闭环设计过程. 图8为PI控制的闭环结构图,其中C(s)是用零极点形式表示的PI控制器,kp为比例增益.为了选择输出响应的最好的位置,在图9中研究了零点ki/kp的位置的影响. 图9是不同的ki/kp对应的根轨迹,把PI控制器的零点相对于靠近原点的输出滤波器的极点实部-rL0/2L0在实轴上进行移动,越向左边平面移动,对闭环极点和振荡的影响越小. 图10是闭环的阶跃响应,当ki/kp比值高时,响应速度加快,调节时间短,但是有震荡,稳定性降低;低值时闭环稳定度高但反应迟钝,kp的变化对调节时间影响小,所以,需要牺牲一定程度的稳定性,设置较高的ki/kp比值. 图10 输出电压控制的闭环阶跃响应Fig.10 Closed-loop step response of the output voltage control 实验电路的连接框图如图11所示,以DSP(TMS320F28335)为控制器,通过A/D转换将测量的模拟量转换成数字量用于DSP的闭环控制计算,输出驱动信号控制逆变器的开关调节逆变器输出电压,调节电流达到控制输出电压的目的. 图11 实验电路连接框图Fig.11 onnection diagram of the experimental circuit 实验结果如图12所示,从图12(a)可以看出启动时间小于20 ms,启动速度快;图12(b)显示输出电压突变后,能在15 ms左右迅速达到稳定值,响应速度快;图12(c)中可以看出负载突变时,电压畸变小,图12(c)中电压畸变约5%,15 ms左右又快速达到稳定值. 通过实验研究可知: (1) 本文提出的双环控制策略启动速度快. (2) 电压突变的实验中,双环控制可以实现快速跟踪电压的变化,迅速稳定在期望值;同时内环滑模控制能够完成对原边电流的快速调节. (3) 当负载突变时,电压畸变小且到达稳定时间短,证明了控制策略的鲁棒性强,由于负载变化时,反馈到原边的等效电阻值也会变化,同时也证明了原边滑模控制的鲁棒性. (a) 系统输出电压v0从0~60 V的启动 ① v0从60^30 V再变到60 V的波形② 局部放大图(b) 输出电压变电压时的波形① v0为30 V时,负载在70^50^70 Ω变化时的波形② 局部放大图(c) 负载变化时的波形 图12 不同条件下实验结果Fig.12 Experimental results under different conditions 本文针对感应耦合电能传输系统,设计了双闭环控制策略,传统的双闭环PI控制算法,控制参数为常数且较为敏感,在系统启动和负载变动时,存在动态响应速度慢、抗干扰性能差的缺点,本文算法能够较好解决这些问题.以滑模控制作为电流内环的双环控制,对参数变化和外部扰动不敏感,具有动态响应速度快、抗干扰能力强、实现容易等优点,通过实验,在系统启动、负载突变、输出参考电压突变下,设计的双环控制有较快的系统响应速度,抗干扰性也比较强,可以满足输出电压稳定的要求.因此,本文所述的双环控制策略有良好的控制效果和实用价值. [1] 程时杰,陈小良,王军华,等. 无线输电关键技术及其应用[J]. 电工技术学报,2015,30(19): 69-83. CHENG Shijie, CHEN Xiaoliang, WANG Juhua, et al. Key technologies and applications of wireless power transmission[J]. Transactions of China Electrotechnical Society, 2015, 30(19): 69-83. [2] 黄学良,谭林林,陈中,等. 无线电能传输技术研究与应用综述[J]. 电工技术学报,2013,28(10): 1-12. HUANG Xueliang, TAN Linlin, CHEN Zhong, et al. Review and research progress on wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 1-12. [3] 王念春,徐发喜,程明. 基于状态空间的逆变器数字双环控制技术研究[J]. 中国电机工程学报,2013,26(增刊1): 166-170. WANG Nianchun, XU Faxi, CHENG Ming. Study on digital dual-loop control for inverters based on the state space[J]. Proceedings of the CSEE, 2013, 26(Sup.1): 166-170. [4] 唐诗颖,彭力,康勇. 脉宽调制逆变电源数字双环控制技术研究[J]. 中国电机工程学报,2009,29(15): 55-60. TANG Shiying, PENG Li, KANG Yong. Research on dual-loop digital control technique for pulse width modulation inverters[J]. Proceedings of the CSEE, 2009, 29(15): 55-60. [5] 马辉,谢运祥. 基于滑模变结构的 Vienna 整流器新型双闭环控制策略研究[J]. 电工技术学报,2015, 30(12): 144-151. MA Hui, XIE Yunxiang. A novel dual closed-loop control strategy based on sliding-mode variable structure of Vienna-type rectifier[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 144-151. [6] LOH P C, NEWMAN M J, ZMOOD D N, et al. A comparative analysis of muti-loop voltage regulation strategies for single and three phase UPS systems[J]. IEEE Trans on Power Electronics, 2003, 18(9): 1176-1185. [7] ZAHID Z U, DALALA Z M, ZHENG C, et al. Modeling and control of series-series compensated Inductive power transfer system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(1): 111-123. [8] ADITYA K, WILLIAMSON S S. Comparative study of series-series and series-parallel compensation topologies for electric vehicle charging[C]∥2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE). Istanbul: IEEE, 2014: 426-430. [9] 侯波,穆安乐,董锋斌,等. 单相电压型全桥逆变器的反步滑模控制策略[J]. 电工技术学报,2015,30(20): 94-99. HOU Bo, MU Anle, DONG Fengbin, et al. Back stepping sliding mode control strategy of single-phase voltage source full-bridge inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 94-99. [10] 刘庆丰,冷朝霞,孙晋坤,等. 基于简化统一模型的DC-DC开关变换器数字优化控制策略[J]. 电工技术学报,2012,27(6): 118-125. LIU Qingfeng, LENG Zhaoxia, SUN Jinkun, et al. A novel digital optimal control for DC-DC converters based on simplified unified model[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 118-125. [11] ABOUSHADY A A, AHMED K H, FINNEY S J, et al. Linearized large signal modeling, analysis, and control design of phase-controlled series-parallel resonant converters using state feedback[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3896-3911. [12] CALISKAN V A, VERGHESE G C, STANKOVIC A M. Multi-frequency averaging dc/dc converters[J]. IEEE Trans. on Power Electron, 1999, 14(1): 124-133. [13] SANDERS R, NOWOROLSKI J M, LIU X Z, et al. Generalized averaging method for power conversion circuits[J]. IEEE Trans. on Power Electron, 1991, 6(2): 251-259. [14] YE Z M, JAIN P K, SEN P C. Modeling of high frequency resonant inverter system in phasor domain for fast simulation and control design[C]∥2008 IEEE Power Electronics Specialists Conference. Rhodes: IEEE, 2008: 2090-2096. [15] YE Z M, JAIN P K, SEN P C. Multiple frequency modeling of high frequency resonant inverter system[C]∥2004 IEEE 35th Annual Power Electronics Specialists Conference. [S.l.]: IEEE, 2004: 4107-4113. [16] WAI R J, LIN F J. Fuzzy neural network sliding mode position controller for induction servo motor drive[J]. In IEE Proceedings-Electric Power Applications, 1999, 146(3): 297-308. [17] 戴斌. 基于滑模变结构控制感应加热的研究[D]. 西安:西安理工大学,2007. [18] 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京:清华大学出版社,2005: 66-68.1.2 系统副边建模







2 双环控制策略

2.1 电流内环控制设计
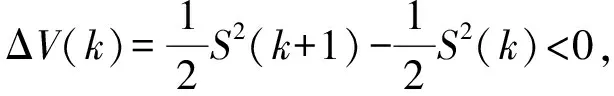
2.2 电压外环控制设计




3.2 实验验证



4 结 论

