横通道设置对车隧气动多波峰的影响
王英学, 任文强, 骆 阳, 何 俊
(西南交通大学交通隧道工程教育部重点实验室, 四川 成都 610031)
列车突入隧道时,会在隧道内产生压缩波,并在隧道出口形成微气压波释放,影响洞口周围环境[1-2].
文献[3-4]中分析了隧道缓冲结构的设计参数及降低压力梯度的理论,得出一些缓冲结构设计的规律、方法.文献[5]中论述了国外有关治理车隧气动效应的治理措施及微气压波的放大现象,并对我国高铁隧道设计参数的选取进行了探讨.
由于微气压波存在放大效应,仅在洞口设置缓冲结构有时难以满足控制微气压波要求.实际中,在隧道主洞两侧开设支洞,以加快工程进度,在不增加工程投资的情况下,可以起到控制微气压波的目的.
对于横通道在缓解微气压波中的应用,一些学者已经进行了研究.文献[6]中对隧道支洞缓解微气压波效果进行研究和测试,微气压波压力峰值与隧道出口附近洞内压缩波梯度峰值成正比,表明隧道支洞可以起到缓解微压波的效果.文献[7-9]中分析了横通道缓解微压波效果,并对结构参数进行了优化.
本文将采用理论分析和数值方法,对隧道设置横通道后的压力曲线进行分析,探讨分析曲线波动机理,通过压力梯度讨论横通道对微气压波的影响.以期更好地指导工程设计.
1 隧道支洞缓解微气压波机理
在实际工程中,为加快施工进度所修建的支洞形式多种多样,可以采用单侧或双侧布置,横通道可以是单个或多个.对于横通道设施各个支洞的名称,一般将平行于隧道主洞的通道称为平导(即平行导洞),与隧道和平导垂直的支洞称为横通道.
横通道及平导使隧道洞口区段所产生的气动效应复杂化[10].横通道的功能与竖井、斜井等的功能类似,只是竖井、斜井距离隧道入口的距离相对较远[11].文献[12]中对压缩波经过竖井的气动机理进行分析,明确了压缩波在竖井与隧道交叉点的传播、反射特性.
基于对竖井的入射波反射规律的分析,可以确定横通道压力波的传播规律,将横通道的气动压力变化分为3个阶段:
(1) 首波传播及泄压(首波标记为①,压缩波为实线,膨胀波为虚线,下同)
该过程是首波到达横通道处的压力释放过程,与竖井的传播过程一致.
列车进入隧道产生压缩波,传播到竖井与隧道连接处时,一部分波以反号波反射,另一部分波则以2个同号波向前传播,如图1(a)所示,图中:lh为横通道距离隧道洞口;dh为主洞与平导间距.当沿横通道向外传播的波到达横通道出口时,以反号波反射回来,向隧道入口传播的波到达隧道入口也产生同样反射,如此往复传播.
(2) 2次波产生与传播
列车到达横通道处,由于空间突变,列车经过再次形成压缩波.该波分为2个分支,隧道主洞部分(标记为②)和横通道部分(标记为③),均为压缩波,如图1(b)所示.
(3) 2次波反射
分配到横通道中的压缩波,到达横通道外开阔空气域转变为膨胀波,向隧道方向传播,在横通道与隧道连接处分为3支:隧道入口方向(膨胀波)、隧道出口方向(膨胀波)和反射回横通道方向(转换为压缩波).
分配到隧道入口方向传播的膨胀波到达隧道入口处,释放部分能量后,转为压缩波向隧道出口方向传播.当传播经过横通道时,其传播、反射与首波的特征一致.由于该波为压缩波,因此,可引起隧道内压力升高,使压力梯度波形曲线出现正压波峰.

(a) 首波
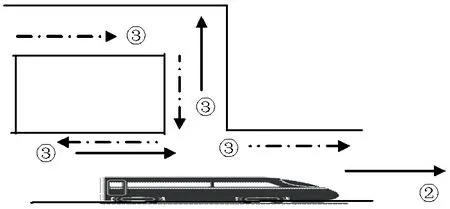
(b) 2次波产生、传播与反射图1 横通道气动压力变化Fig.1 Compression wave transmission and reflection at cross adit
2 数值分析
2.1 紊流模型的选取及列车进入隧道过程的实现
在流体分析时,紊流模型的选取对计算结果有很大影响,可选的紊流模式也较多.直接数值模拟(direct numerical simulation, DNS)不用任何湍流模型,直接求解完整的三维非定常的N-S方程组.雷诺平均模型(Reynolds-averaged Navier-Stokes equations, RANS)应用紊流统计理论,将非稳态的N-S方程对时间做平均,其工程应用的紊流模型有雷诺应力模型(Reynolds stress model,RSM),该模型把所有尺度的雷诺应力都使用模型进行模拟.大涡模拟(large eddy simulation, LES)中,动量、能量、质量及其标量主要由大涡输送,对大涡及小涡采取不同处理策略,进行流场的分析计算.在k-ε模型中,主要求解紊动能和耗散率方程模拟紊流状态.
许多学者在车隧气动分析中,所选取的紊流模型也略有差别,比较常用的有k-ε模型[13]、Les模型[14]等.大涡模型紊流模型被认为是具有应用前景的紊流模式.
本文利用商用工程软件Ansys中的Fluent模块,开展列车进入隧道气动过程的模拟分析.紊流模型选用大涡模型(LES),计算中介质采用理想气体.考虑到大涡模型对网格的质量要求较高,在建模及网格划分时,对车头、隧道入口等一些关键部位进行了网格加密处理.
采用Fluent模块中的动网格法[15]可以模拟列车-隧道之间的相对运动,文献[7,11-12,16-17]中采用该方法进行模拟分析,取得了良好效果.本文也将采用该方法,模拟列车通过隧道过程.研究结果表明,本文的计算结果与现场测试数据[18]的压缩波压力峰值接近,表明选取的模型是正确的.
2.2 计算参数
在计算中,列车采用CHR3型动车,机车横截面积为11.624 m2.车长为100 m,车速vc=350 km/h.隧道面积为100 m2,时速350 km/h双线隧道标准设计断面.隧道洞口设置1个横通道,lh=20 m,dh=15 m,横通道面积为29 m2,平导段隧道面积为35 m2.模型的隧道长度为500 m,隧道两端空气域长度为300 m,列车距离隧道入口为100 m,隧道及横通道布置如图2所示.
2.3 数值模型及网格划分
在计算中,模型的最小网格尺寸为0.02 m×0.02 m,并在某些关键区域进行了网格细化.隧道出入口区域采用无反射边界,车头、隧道、横通道模型网格如图3所示.计算中的迭代次数为7次,计算步长为0.000 5 s,最大残差0.001.

图2 数值计算中隧道及横通道布置示意(单位:m)Fig.2 Tunnel and cross adit setting dimension in numeral simulation (unit: m)

(a) 列车车头

(b) 隧道入口及横通道图3 数值计算模型网格划分Fig.3 Numeral simulation mesh
2.4 计算结果
通过计算,得到在无横通道时,距离隧道洞口10、15、20 m时隧道内测点压力及压力梯度监测曲线,如图4所示.横通道距离隧道入口20 m,设置横通道后,隧道内距隧道入口200 m处测点压力及压力梯度曲线如图5所示,各曲线的压缩波及压力梯度峰值如表1所示.
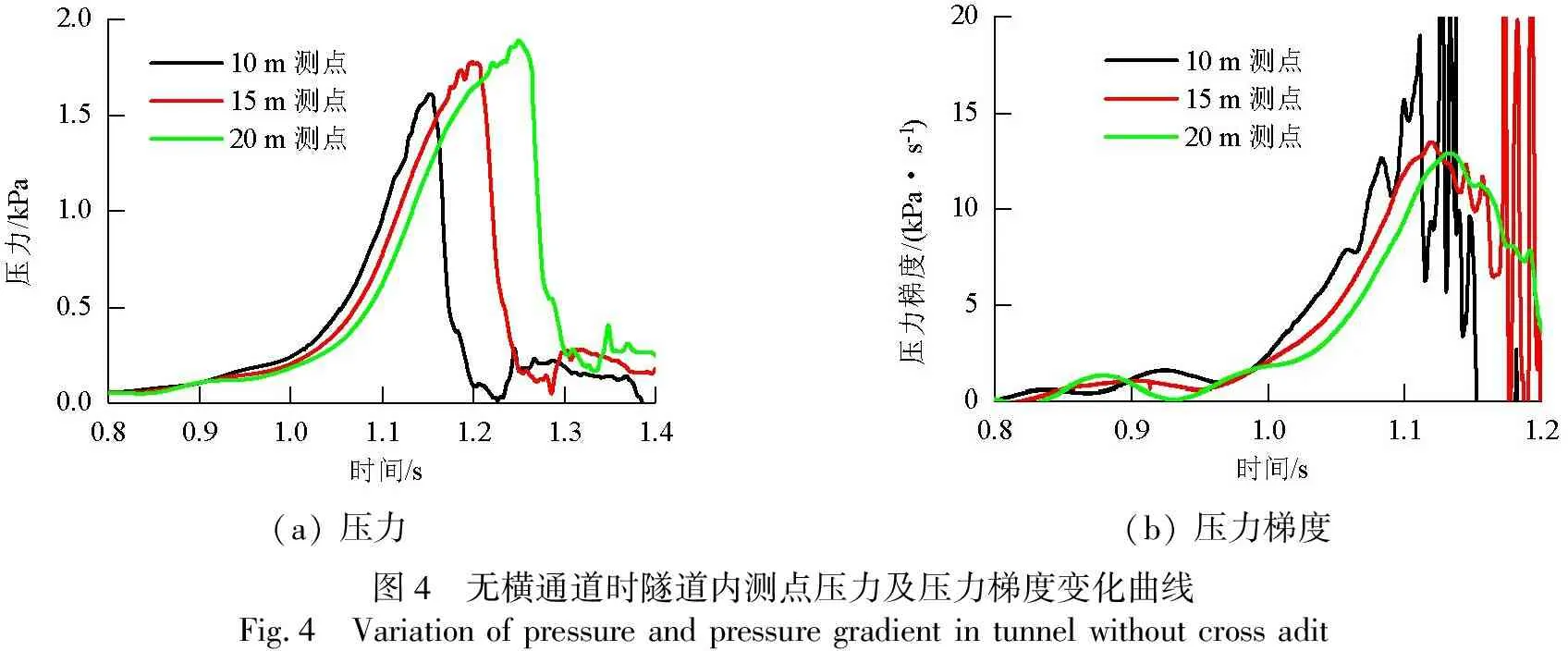
(a) 压力(b) 压力梯度图4 无横通道时隧道内测点压力及压力梯度变化曲线Fig.4 Variation of pressure and pressure gradient in tunnel without cross adit

(a) 压力(b) 压力梯度图5 隧道内测点压力及压力梯度曲线Fig.5 Variation of pressure and pressure gradient in tunnel

表1 隧道内测点压力及压力梯度峰值Tab.1 Pressure and pressure gradient peak value in tunnel
2.5 计算结果分析
2.5.1波动曲线
从有、无横通道的压力及压力梯度曲线可知:
(1) 压力梯度在列车进入隧道较短距离即达到峰值,压缩波在列车完全进入隧道前一直增加.
列车进入隧道10~20 m过程中,压缩波处于上升期,曲线峰值是逐渐增加的(如图4(a)),而压力梯度很快上升,在10 m左右已经达到峰值(如图4(b)).
(2) 隧道设置横通道与无横通道相比,压力曲线波动相差较大,会出现次级波峰、波谷.
在无横通道时,隧道内200 m处压力梯度可分为3段:迅速上升区段、平缓上升区段、迅速下降区段.迅速上升区段为列车头部段突入隧道所产生;平缓上升区段为列车车身进入隧道阶段所产生;迅速下降区段为列车车尾进入隧道所产生的膨胀波所引起.设置横通道以后,隧道内200 m处压缩波曲线的迅速上升区段和迅速下降区段与无横通道的情况基本一致;在平缓上升区段则出现多个波峰、波谷.
2.5.2压力曲线多波出现机理
(1) 首波、2次波峰值压力梯度峰值形成距离差异无论是压缩波还是压力梯度,要到达峰值都需要一定时间,为更好分析压力梯度多峰值出现机理,假定列车进入隧道形成首波压力梯度峰值所需距离为x1,列车经过横通道形成2次波峰值所需距离为x2.根据前面对洞口多测点压力梯度对比,取x1=10 m.图6为压力波在隧道内传播到达时刻计算简图.

图6 隧道内测点压力波动特性分析简图Fig.6 Calculation graph of pressure variation at measure point in tunnel
计算中,横通道距离隧道入口lh=20 m,横通道在隧道方向宽度wh=5.9 m,压缩波传播速度为vb=340 m/s.以隧道入口为时间起始点,则首波和2次波分别到达隧道内P处距离所用时间为
t1=x1/vc+(lh-x1+wh+x2+x)/vb,
(1)
t2=(lh+wh+x2)/vc+x/vb,
(2)
Δt1=t2-t1=(lh+wh+x2)/vb+x/vb-
x1/vc-(lh-x1+wh+x2+x)/vb=
(lh+wh+x2-x1)/vc-
(lh+wh+x2-x1)/vb.
记Δx=x1-x2,则有
Δt1=(lh+wh-Δx)/vc-(lh+wh-Δx)/vb,
Δx=((lh+wh)(1/vc-1/vb)-Δt1)/
(1/vc-1/vb).
经计算得到,隧道内200 m测点处首波、2次波压力梯度峰值出现时刻分别为t1=1.648 s,t2=1.826 s,则,Δt1=0.178 s.计算得到Δx=1.7 m,x1>x2.
(2) 2次波波谷
2次波波谷产生的原因可能有两种:
① 列车进入隧道所形成的首波分配到横通道的压缩波分支,传播至横通道出口后,反射成为膨胀波向隧道方向传播.该膨胀波到达横通道与隧道交叉处,又分为3支:第1支转换为压缩波又向横通道出口传播;第2支作为膨胀波向隧道入口方向传播;第3支作为膨胀波向隧道出口方向传播,该分支正是产生2次波波谷的原因.
在该情况下,引起2次波波谷的波源与隧道内首波是一致的,只是行走路径不同,在横通道内有1个折返的过程,于是得到横通道反射膨胀波与首波历程时间差.
以横通道的中心线作为波的传播路径,隧道入口为时间起算点,则有
t1=x1/vc+(lh-x1+wh+x2+x)/vb,
(3)
t2=x1/vc+(lh-x1)/vb+2(wh+dh+lh)/vb+
(x2+x)/vb.
(4)
于是有
Δt2=2(dh+lh)/vb+wh/vb=0.223 s.
② 列车到达横通道时,产生2次波在隧道内传播的同时,在横通道内也产生压缩波.该横通道压缩波传播至横通道出口后,反射成为膨胀波向隧道方向传播.该膨胀波到达横通道与隧道交叉处,又分为3支:第1支转换为压缩波又向横通道出口传播;第2支作为膨胀波向隧道入口方向传播;第3支作为膨胀波向隧道出口方向传播,该分支正是产生2次波波谷的原因.
在该情况下,引起2次波波谷的波源是由列车到达横通道时诱发引起的压缩波,在横通道内传播并折返的过程.于是得到横通道反射膨胀波与首波历程时间差.
以横通道的中心线作为波的传播路径,隧道入口为时间起算点,则有
t1=x1/vc+(lh-x1+wh+x2+x)/vb,
(5)
t2=(lh+wh)/vc+2(dh+lh)/vb+
(x2+x)/vb.
(6)
于是有
Δt2=(lh+wh-x1)/vc+
(2dh+lh+x1-wh)/vb=0.323 s.
由计算曲线上检测到的Δt2=0.314 s.所以,第2种诱发原因更为合理.
(3) 横通道产生压缩波的2次反射波(压缩波).
对2次波波谷的分析表明,从横通道传播到隧道都是膨胀波.在监测曲线中看到有第3个波峰,而波峰一定是压缩波所引起的,其产生原因为分配到横通道中的压缩波,经横通道出口及隧道入口反射,再次向隧道出口方向传播的压缩波.
参考图6,首波及该压缩波到达隧道内测点P的时刻为
t1=x1/vc+(lh-x1+wh+x2+x)/vb,
(7)
t2=(lh+wh)/vc+2(dh+lh)/vb+
(2lh+wh)/vb+(x2+x)/vb.
(8)
于是有
Δt3=(lh+wh-x1)/vc+
(2dh+3lh+x1)/vb=0.457 s.
实际检测曲线的时间差为Δt3=0.45 s.
上述计算,隧道内测点压力梯度峰值出现时间差如表2所示.
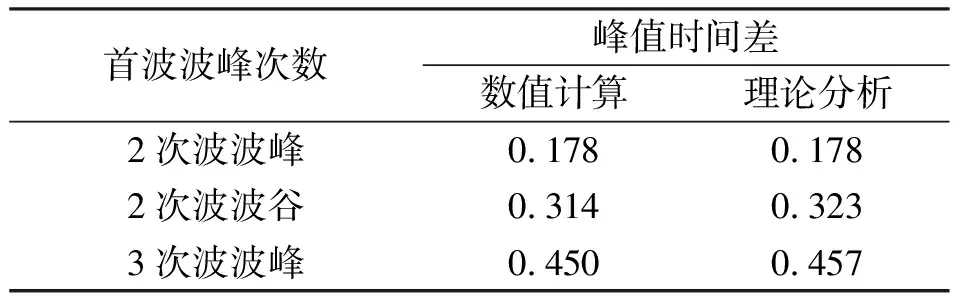
表2 压力梯度多波峰出现时刻对照表Tab.2 Pressure gradient multiple peak appearing period comparison table s
2.6 压力波传播特性应用
通过分析可知,列车在经过的设置横通道后,隧道内压力出现多波峰、波谷的原因是在横通道处压缩波、膨胀波的传播、反射.利用这些特性,可以更好理解压力梯度曲线中波峰、波谷的产生原因.
针对第3压力梯度峰值,可知横通道的不利位置.分析思路如下.
当压缩波首波分配到横通道内的分支,传播到达横通道出口,反射到达横通道与隧道交叉点处时刻与列车经过该点时刻重合,会使分配到横通道的压缩波叠加,则有
(9)
算例中,x1=10 m,dh=15 m,则lh=49 m.
lh=50 m和lh=20 m时的压力梯度对比分析曲线如图7所示.


(a) 压力

(b) 压力梯度图7 不同横通道设置位置时隧道内测点压力及压力梯度曲线(测点距隧道入口200 m)Fig.7 Pressure and pressure gradient curve at measure point in tunnel with different cross adit setting position( the measure point is 200 m to tunnel entrance )
P2=6.6 kPa/s,P3=5.3 kPa/s.


3 结 论
在设置的横通道条件下,通过对车隧气动特性的理论分析和数值模拟,得到如下结论:
(1) 在列车进入隧道过程中,压缩波压力达到峰值需要较长时间,在列车车体进入隧道过程中一直是增加的,而压力梯度达到峰值所需时间较短,在列车进入隧道10 m左右,即达到峰值.
(2) 列车进入隧道形成首波压力梯度峰值所需运行距离要略大于列车经过横通道形成2次压力梯度波峰值所需运行距离;
(3) 列车经过横通道时,在横通道内也产生压缩波,其反射、传播影响隧道内压力梯度多个波峰、波谷的出现和峰值的大小.
(4) 随着横通道距隧道入口距离增大,列车经过横通道所产生的次级压力波动效应会有所降低.横通道位置设置在50 m与设置在20 m处相比,首波压力梯度峰值基本不变,但次级波的压力梯度峰值更小.
[1] 赵文诚,高波,漆泰岳. 高速铁路隧道出口微压波及其主被动减缓措施[J]. 石家庄铁道学院学报,2004,17(3): 5-9.
ZHAO Wencheng, GAO Bo, QI Taiyue. Micro-pressure wave around high-speed railway tunnel exit and active and passive method of reduction[J]. Journal of Shijiazhuang Railway Institute, 2004, 17(3): 5-9.
[2] 赵文成,高波,王英学. 高速铁路隧道口微压波减缓措施分析[J]. 地下空间与工程学报,2005(2): 274-277.
ZHAO Wencheng, GAO Bo, WANG Yingxue. Analysis of the mitigation methods of micro-pressure wave generated around high-speed railway tunnel exits[J]. Chinese Journal of Underground Space and Engineering, 2005(2): 274-277.
[3] HOWE M S, LIDA M, MAEDA T T, et al. Aero-acoustics of a tunnel-entrance hood with a rectangular window[J]. Journal of Fluid Mechanics, 2003, 4(8): 211-243.
[4] HOWE M S. Design of a tunnel-entrance hood with multiple windows and variable cross-section[J]. Journal of Fluids and Structures, 2003, 17(8): 1111-1121.
[5] 王建宇. 列车通过隧道时诱发的空气动力学问题和高速铁路隧道设计参数[J]. 世界隧道,1995(1): 3-13.
[6] YAMAMOTO A, OZAWA S, MAEDA T. Reduction of micro-pressure wave radiated from tunnel exit by side branches in tunnel[J]. Quarterly Report of Rail way Technical Research Institute of Japanese National Rail Ways, 1984, 25(3): 102-105.
[7] 李志伟,梁习锋,张键. 横通道对缓解隧道瞬变压力的研究[J]. 铁道科学与工程学报,2010,7(4): 37-41.
LI Zhiwei, LIANG Xifeng, ZHANG Jian. Study of alleviating transient pressure with cross passage in a tunnel[J]. Journal of Railway Science and Engineering, 2010, 7(4): 37-41.
[8] 蒲佳. 竖井、横通道对高速铁路隧道出口微压波影响分析[D]. 成都:西南交通大学,2009.
[9] 戴文,高波,赵文成. 高速铁路隧道横通道气动效应研究[J]. 铁道建筑,2011(12): 57-60.
DAI Wen, GAO Bo, ZHAO Wencheng. Study on aerodynamic effects in cross passage of high speed railway tunnel[J]. Railway Engineering, 2011(12): 57-60.
[10] 岳楹沁,高波. 横通道对隧道出口微压波影响的数值模拟研究[J]. 华东交通大学学报,2006,23(5): 20-23.
YUE Yingqin, GAO Bo. Study of the Influence over cross passage on high-speed railway tunnel exit micro-pressure wave[J]. Journal of East China Jiaotong University, 2006, 23(5): 20-23.
[11] 刘佩斯. 竖井对高速铁路隧道气动效应的影响研究[D]. 成都:西南交通大学,2009.
[12] 骆建军,高波,王英学,等. 高速列车穿越有竖井隧道流场的数值模拟[J]. 西南交通大学学报,2004,39(4): 442-446.
LUO Jianjun, GAO Bo, WANG Yingxue, et al. Simulation of unsteady three-dimensional flow induced by high-speed train entering tunnel with shaft[J]. Journal of Southwest Jiaotong University, 2004, 39(4): 442-446.
[13] 骆建军,吴尽,陈鹏飞. 高速铁路并联隧道横通道对隧道内压力变化的影响[J]. 北京交通大学学报,2015,39(1): 8-13.
LUO Jianjun, WU Jin, CHEN Pengfei. Pressure change from the cross aisle when the train passing through parallel tunnel of high-speed railway[J]. Journal of Beijing Jiaotong University, 2015, 39(1): 8-13.
[14] 马静,张杰,杨志刚. 横风下高速列车非定常空气动力特性研究[J]. 铁道学报,2008,30(6): 109-114.
MA Jing, ZHANG Jie, YANG Zhigang. Study on the unsteady aerodynamic characteristics of a high-speed train under cross wind[J]. Journal of the China Railway Society, 2008, 30(6): 109-114.
[15] 张来平,邓小刚,张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展,2010,40(4): 424-447.
ZHANG Laiping, DENG Xiaogang, ZHANG Hanxin. Reviews of moving grid generation techniques and numerical methods for unsteady flow[J]. Advances in Mechanics, 2010, 40(4): 424-447.
[16] 赵文成,高波,骆建军. 高速列车通过隧道的三维数值模拟[J]. 中国铁道科学,2003,24(5): 96-100.
ZHAO Wencheng, GAO Bo, LUO Jianjun. Three-dimensional numerical simulation of high-speed trains passing through tunnel[J].China Railway Science, 2003, 24(5): 96-100.
[17] 王英学,高波,陆振华,等. 隧道中部存在车站时列车会车气动效应数值分析[J]. 空气动力学学报,2009,27(3): 369-372.
WANG Yingxue, GAO Bo, LU Zhenhua, et al. Aerodynamics effect numeral simulation of high speed train passing through tunnel with mid-station[J]. Acta Aerodynamica Sinica, 2009, 27(3): 369-372.
[18] 赵有朋,马伟斌,程爱君,等. 高速铁路隧道气动效应[M]. 北京:中国铁道出版社,2012: 139-144.

