高考解答题精选

■本刊编辑部

1.在锐角△A B C中,角A,B,C所对的边分别为a,b,c,已知s i n

(1)求t a n2的值;

(2)若a=2,求b的值。

2.已知公差不为零的等差数列{an},满足a1+a3+a5=9,且a1,a4,a16成等比数列。

(1)求数列{an}的通项公式;

(2)设求数列{b}的前

nn项和Sn。

3.甲、乙两人参加某种选拔测试。在备选的1 0道题中,甲答对其中每道题的概率都是,乙能答对其中的5道题。规定每次考试都从备选的1 0道题中随机抽出3道题进行测试,答对一题加1 0分,答错一题(不答视为答错)减5分,得分最低为0分,至少得1 5分才能入选。求：

(1)乙得分的分布列和数学期望;

(2)甲、乙两人中至少有一人入选的概率。

4.已知正三棱柱A B C-A'B'C',如图1所示,其中G是B C的中点,D,E分别在线段常数λ,记点M的轨迹为曲线C。

(1)求曲线C的方程,并讨论C的形状与λ值的关系;

(2)若,m=1时,得到的曲线为C1,将曲线C1向左平移一个单位得到曲线E,过点P(-2,0)的直线l1与曲线E交于不同的两点A(x1,y1),B(x2,y2),过F(1,0)的直线A F,B F分别交曲线E于D,Q两点,设α,β∈R,求α+β的取值范围。

6.已知函数f (x)=l nx-x2+a x,x1,x2是函数f (x)的两个零点,且x1＜x2。

(1)讨论函数f (x)的单调性;

(2)求a的取值范围;

(3)设f'(x)是函数f (x)的导函数,求证

1.(1)在锐角△A B C中,A+B+C=π,

故

(2)因为

将c2-2b cc o sA(余弦定理)中,得b4-6b2+9=0,解得

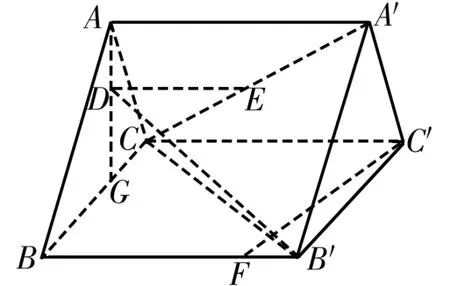
图1

2.(1)因为a1+a3+a5=9,所以3a3=9,A G,A'C上运动,使得D E∥平面B C C'B',F是B B'上的一点,且C C'=2B C=8B'F=4。

(1)求证：C'F⊥B'D;

(2)求二面角A'-B'C-C'的余弦值;

(3)求线段D E的最小值。

5.设动点M到坐标原点O的距离和它到直线l：x=-m(m＞0)的距离之比是一个所以a3=3。

因为a1,a4,a16成等比数列,所以a24=a1a16,(3+d)2=(3-2d)(3+1 3d),因为d≠0,则d=1。所以an=a3+(n-3)d=3+(n-3)=n。

(2)由(1)得：

3.(1)设乙得分为ξ,则ξ=0,1 5,3 0。

所以ξ的分布列如表1所示。

表1

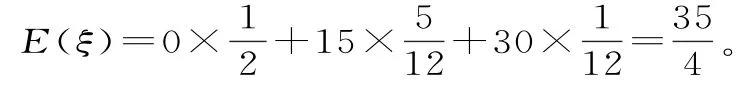
(2)设“甲入选”为事件A,“乙入选”为事件B,则故所求概率P=1-

4.(1)如图2,连接B'G。因为G是B C的中点,所以A G⊥B C,所以A G⊥平面B B'C'C。因为C'F⊂平面B B'C'C,所以A G⊥C'F。

图2

又∠C'B'B=所以△C'B'F∽△B'B G,所以B'G⊥C'F。因为A G∩B'G=G,所以C'F⊥平面A B'G。因为B'D⊂平面A B'G,所以C'F⊥B'D。

(2)如图2,以G为坐标原点,G B、G A所在直线分别为x轴,z轴,建立空间直角坐标系,则G(0,0,0),B(1,0,0),B'(1,4,0),A'(0,4,),C(-1,0,0),A(0,0,)。所以

设平面A'B'C的法向量为m=(x,y,z),则即

令,得则平面 的A'B'C一个法向量为m=(2 3,-3,2)。

又平面B'C C'的一个法向量为n=(0,0,1),故所求二面角的余弦值为c o s＜m,n＞=

(3)由题意,可设D(0,0,k)(0≤k≤

由故E(λ-1,4λ所以=(λ-1,4λ,3λ-k)。易知为平面B C C'B'的一个法向量。

因为D E∥平面B C C'B',所以

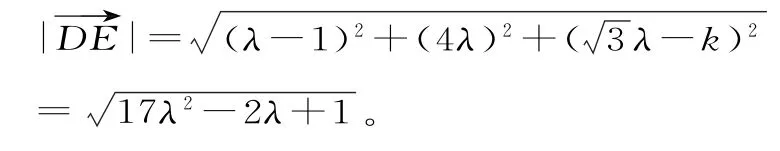
又故当时,线段D E有最小值

5.(1)设M(x,y),由题设有故曲线C的方程为(1-λ2)x2+y2-2m λ2x-m2λ2=0。

①λ=1时,曲线C的方程为：y2=2m·(x+m)是抛物线。

②λ≠1时,曲线C 的方程为

λ＞1时,曲线C的方程为焦点在x轴上的双曲线;0＜λ＜1时,曲线C的方程为焦点在x轴上的椭圆。

当x∈(0 ,x0)时,f'(x)＞0,f (x)单调递增;当x∈(x0,+∞)时,f'(x)＜0,f (x)单调递减。

(2)由于函数f (x)存在两个零点,所以f (x)max＞0。

由(1)可知f (x)max=f (x0)=l nx0-+a x0,且

所以f (x)max=l nx0-+-1=l nx0+-1＞0。

由于g (x0)=l nx0+-1在(0,+∞)上为增函数,且g(1)=0,所以

所以a的取值范围是(1,+∞)。

(3)由于x1,x2是函数f (x)的两个零点,且x1＜x2,所以l nx1-+a x1=0,l nx2-+a x2=0。